Pendule cycloïdal

Pendule cycloïdal
Pendule cycloïdal

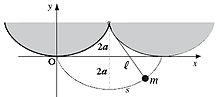
Dans un pendule cycloïdal, un petite masse pesante glisse sans frottement dans une cuvette en forme d'arche de cycloïde concave ayant pour base l'axe horizontal Ox.

Elle y oscille sinusoïdalement avec une pulsation

\omega_0 = \sqrt {\frac {g}{4a}}

, quelle que soit l'amplitude des oscillations : l'oscillation est tautochrone.

Huygens découvre (1659) cette propriété et pense avoir trouvé là de quoi fabriquer une horloge remarquable, mais il n'en est rien.


Sommaire

Les oscillations du pendule cycloïdal sont sinusoïdales

En effet, le mouvement curviligne, s(t), satisfait l'équation différentielle : \dot s^2 + \omega^2_0 s^2 = cste :

s^2 = 8 ay~
Démonstration

On choisit l'origine au bas de l'arche de la cycloïde :

x= au +a \sin u~ et y = a -a \cos u~.

Prendre a comme unité. Soit s l'abscisse curviligne, comptée à partir de O ; alors la cycloïde est la courbe telle que le lemme précédent est vérifié : ds^2 = dx^2 + dy^2 = 2(1+\cos u) du^2 = 4 \cos^2 u/2 ~ ,soit ds = 2 \cos u/2~ ; d'où s = 4 \sin u/2 ~ (résultat de Wren(1658), ce résultat est obtenu par simple considération géométrique : Wallis publie immédiatement cette rectification remarquable car Pascal en août 1658 en avait lancé le défi, sous le nom de Dettonville). Soit s^2 = 8(1-\cos u)~ . Rétablir la valeur de a. D'où le lemme ; la réciproque est vraie.

  • Appliquer alors le théorème de l'énergie-cinétique :
v^2/2 + g y = cste ~
  • soit \dot s^2 + (g/4a) \cdot s^2 = cste : On reconnaît l'équation différentielle d'une oscillation sinusoïdale de pulsation
\omega_0 = \sqrt { g/4a}

.

  • remarque : le cercle surosculateur (externe) à la cycloïde en O est de rayon 4a ; le résultat est conforme à la théorie des petites oscillations du pendule simple ordinaire.

Du pendule à la pendule

  • Huygens travaille à fabriquer une pendule d'abord avec un pendule simple. On sait depuis Mersenne (1638) que les oscillations ne sont pas isochrones (le fameux rapport 41/40 pour une amplitude de 90°). Huygens a donc l'idée de raccourcir la longueur de la ficelle aux fortes amplitudes en interposant au sommet deux flasques circulaires : alors la trajectoire est formée de deux arcs de développante de cercle. Le concours ouvert par Pascal en 1658 sur la cycloïde, dont la réponse lui est communiquée en février 1659, lui donne l'idée d'essayer des flasques cycloïdales. En décembre 1659, il est fier d'annoncer sa découverte à son maître Frans van Schooten : il a obtenu des oscillations isochrones. En 1673, il publiera son Horologium où il démontrera, entre autres, que la courbe développante d'une cycloïde est une cycloïde : il est alors un des savants les plus célèbres d'Europe (Bientôt, l'heure viendra pour Newton et Leibniz).
  • Certaines franc-comtoises sont encore fabriquées avec une suspension via un feuillard s'appuyant sur deux flasques pseudo-cycloïdales. Mais l'horlogerie ne retiendra pas vraiment le procédé, qui marche bien sur le papier, mais reste impraticable : Airy montrera qu'il vaut bien mieux avoir un couteau d'appui bien défini et assurer une élongation maximale stable et compenser les variations thermiques.
  • Huygens n'arrivera pas à fabriquer le chronomètre de marine espéré : il inventera la montre à ressort spiral ; bien plus tard, Harrison gagnera le concours des longitudes, avec une montre-spiral, la H4 (1773).

Notes et références

Voir aussi

Articles connexes

Liens et documents externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Pendule cycloïdal de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Pendule cycloidal — Pendule cycloïdal Le pendule cycloïdal est le mouvement d un petit anneau de masse , soumis à la pesanteur d intensité , glissant sans frottement sur une cycloïde concave ayant pour base l axe horizontal Ox et suivant l équation : avec u… …   Wikipédia en Français

  • pendule cycloïdal — cikloidinė švytuoklė statusas T sritis fizika atitikmenys: angl. cycloidal pendulum; Huygens pendulum vok. zykloidales Pendel, n; Zykloidenpendel, n rus. циклоидальный маятник, m pranc. pendule cycloïdal, m …   Fizikos terminų žodynas

  • Pendule pesant — composé Pendule pesant simple On appelle pendule pesant tout solide mobile autour d un axe (en principe horizontal) ne pa …   Wikipédia en Français

  • pendule — 1. pendule [ pɑ̃dyl ] n. m. • 1658, Huyghens; cf. funependule (1646); lat. pendulus, de pendere 1 ♦ Sc. Système oscillant de fréquence constante. Pendule simple ou Pendule : masse ponctuelle suspendue à un point fixe par un fil tendu, de masse… …   Encyclopédie Universelle

  • Pendule simple — Schéma montrant un pendule simple. En physique, le pendule simple est une masse ponctuelle fixée à l extrémité d un fil sans masse, inextensible et sans raideur[1] et oscillant sous l effet de la pesanteur. Il s agit du modèle de pen …   Wikipédia en Français

  • Pendule (physique) — Pour les articles homonymes, voir Pendule. Schéma montrant le comportement d un pendule simple. En physique, le pendule est un système oscillant qui, écarté de sa position d équilibr …   Wikipédia en Français

  • cycloïdal — cycloïde [ siklɔid ] n. f. • 1638; du gr. kuklos « cercle » ♦ Math. Courbe engendrée par un point d un cercle roulant sans glisser sur une droite ou sur un autre cercle. Adj. CYCLOÏDAL, ALE, AUX , 1701 . ● cycloïdal, cycloïdale, cycloïdaux… …   Encyclopédie Universelle

  • CYCLOÏDAL, ALE — adj. T. de Géométrie Qui appartient à la cycloïde. Pendule cycloïdal, Pendule dont les oscillations sont rendues isochrones par l’arc de cycloïde que décrit le mobile …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • cycloidal pendulum — cikloidinė švytuoklė statusas T sritis fizika atitikmenys: angl. cycloidal pendulum; Huygens pendulum vok. zykloidales Pendel, n; Zykloidenpendel, n rus. циклоидальный маятник, m pranc. pendule cycloïdal, m …   Fizikos terminų žodynas

  • Puits de potentiel — Pour les articles homonymes, voir Puits. Puits de potentiel unidimensionnel Un puits de potentiel désigne, en physique, le voisinage d un minimum local d é …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”