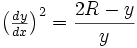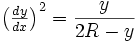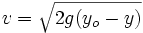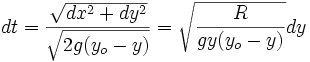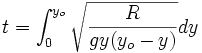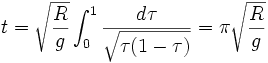Courbe Tautochrone

Courbe tautochrone

Une courbe tautochrone est la courbe où le temps pris par une particule glissant sous l'influence uniforme de la gravité jusqu'à son point le plus bas est indépendant de son point de départ.

Le problème tautochrone, l'essai d'identifier cette courbe, fut résolu par Huygens en 1659 dans le cas où seule la gravité agit. Il prouva géométriquement dans son Horologium oscillatorium (1673) que la courbe était une cycloïde. Cette solution fut utilisée ultérieurement pour attaquer le problème de la courbe brachistochrone.

Plus tard, des mathématiciens tels que Lagrange, d'Alembert et Euler cherchèrent une solution analytique au problème dans le cas général.

Démonstration que la cycloïde est une courbe tautochrone

L’équation différentielle décrivant la cycloïde générée par un cercle de rayon R, est:

$\begin{pmatrix}\frac{dy}{dx}\end{pmatrix}^2=\frac{2R-y}{y}$

Pour l’exercice qui nous intéresse on utilise une cycloïde inversée (tête en bas) dont l’équation différentielle prend la forme:

$\begin{pmatrix}\frac{dy}{dx}\end{pmatrix}^2=\frac{y}{2R-y}$

On place une particule sur la courbe à la position de coordonnées $(x o, y o)$ et on laisse la gravité agir (constante gravitationnelle g). La vitesse en un point quelconque (x, y) de la courbe est:

$v=\sqrt{2g(y_o-y)}$

Le temps pris par la particule pour effectuer le trajet infinitésimal jusqu’au point de la courbe (x+dx, y+dy) est:

$dt=\frac{\sqrt{dx^2+dy^2}}{\sqrt{2g(y_o-y)}}=\sqrt{\frac{R}{gy(y_o-y)}}dy$

Le temps t que prendra la particule pour arriver au bas de la cycloïde est:

$t=\int_0^{y_o}{\sqrt{\frac{R}{gy(y_o-y)}}dy}$

En effectuant le changement de variable 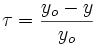$\tau=\frac{y_o-y}{y_o}$ on trouve:

$t=\sqrt{\frac{R}{g}}\int_0^1{\frac{d\tau}{\sqrt{\tau(1-\tau)}}}=\pi\sqrt{\frac{R}{g}}$

D’où il ressort que le temps de trajet est indépendant du point de départ sur la cycloïde.

Note : la démonstration précédente est rarement suivie par une physicienne qui préfère la suivante :

la définition d'une cycloïde en coordonnées (arc s, ordonnée y)

est : s² = k y .

or, d'après le théorème de l'énergie cinétique, (ds/dt)² + 2g.y = cste .

Éliminer la variable y entre ces deux équations conduit à :

(ds/dt)² + n².s² = cste ,

D'où mouvement oscillatoire tautochrone sinusoïdal de pulsation n.

Note : on entend parler parfois de problème isochrone du puits de potentiel. Il est clair qu'un problème tautochrone est isochrone. Par contre, existe-t-il des puits différents qui admettent des oscillations isochrones ? la réponse est non : le seul puits symétrique à avoir une oscillation isochrone est la cycloïde avec par conséquent un mouvement sinusoïdal en curviligne ( et évidemment pas le mouvement en abscisse, en projection sur l'axe Ox, n'est pas sinusoidal ! ). Ceci dit, remarquons que le mouvement en abscisse est bien isochrone ( mais non sinusoidal). De même le mouvement en ordonnée, bien sûr, qui n'est pas non plus sinusoidal ! On remarquera que dans le cas des "puits de potentiel" (ce qui n'est pas le même problème), est mouvement isochrone le mouvement de Kepler dans le puits du potentiel-apparent de Leibniz(1693) : V(r)effectif = L²/2mr² -(GM)m/r. Tous ces puits de potentiel sont-ils reliés entre eux : la réponse est affirmative via la transformée d'Abel.

Portail de la géométrie

Ce document provient de « Courbe tautochrone ».

Catégories : Courbe | Gravitation

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Courbe Tautochrone de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Courbe tautochrone — Illustration. Une courbe tautochrone est la courbe où le temps pris par une particule glissant sous l influence uniforme de la gravité jusqu à son point le plus bas est indépendant de son point de départ. Le problème tautochrone, l essai d… … Wikipédia en Français
courbe tautochrone — tautochrona statusas T sritis fizika atitikmenys: angl. tautochrone; tautochronous curve vok. Tautochrone, f rus. таутохрона, f; таутохронная кривая, f pranc. courbe tautochrone, f; ligne tautochrone, f; tautochrone, f … Fizikos terminų žodynas
tautochrone — [ totokron ] adj. • 1741; de tauto et chrone ♦ Math. Courbe tautochrone, telle que le temps de déplacement d un mobile partant avec une vitesse initiale nulle est indépendant de son point de départ sur la courbe. tautochrone adj. PHYS Syn. de… … Encyclopédie Universelle
Courbe Brachistochrone — Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes … Wikipédia en Français
Courbe brachystochrone — Courbe brachistochrone Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de… … Wikipédia en Français
tautochrone — (tô to kro n ) adj. Qui a lieu en des temps égaux. Courbe tautochrone, ou, substantivement, la tautochrone, courbe telle que, si on laisse tomber un corps pesant le long de sa concavité, il arrivera toujours au point le plus bas dans le même… … Dictionnaire de la Langue Française d'Émile Littré
Courbe rectifiable — Longueur d un arc Camille Jordan est l auteur de la définition la plus courante de la longueur d un arc. En géométrie, la question de la longueur d un arc est intuitivement simple à concevoir. L idée d arc correspond à celle d une ligne, ou d une … Wikipédia en Français
Tautochrone — tautochrona statusas T sritis fizika atitikmenys: angl. tautochrone; tautochronous curve vok. Tautochrone, f rus. таутохрона, f; таутохронная кривая, f pranc. courbe tautochrone, f; ligne tautochrone, f; tautochrone, f … Fizikos terminų žodynas
tautochrone — tautochrona statusas T sritis fizika atitikmenys: angl. tautochrone; tautochronous curve vok. Tautochrone, f rus. таутохрона, f; таутохронная кривая, f pranc. courbe tautochrone, f; ligne tautochrone, f; tautochrone, f … Fizikos terminų žodynas
Courbe brachistochrone — Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Courbe Tautochrone