Dettonville

Le Traité de la Roulette est un ouvrage écrit en 1659 par Blaise Pascal, sous le nom de plume Dettonville.

En 1658, Pascal a 35 ans, et a déjà renoncé à faire une carrière scientifique depuis 1654. Néanmoins sous le pseudonyme de Dettonville, il va proposer un challenge : trouver un certain nombre de propriétés de la cycloïde, autre nom de la roulette, courbe déjà étudiée par Roberval.

Après que Wren en 1658 eut effectué la rectification de la cycloïde, Pascal publiera très vite les challenges d'octobre 1658, puis le livre la Théorie de la Roulette, en janvier 1659.

Cet ouvrage est considéré comme un des derniers traités de Géométrie des Indivisibles, intermédiaire entre la méthode des indivisibles de Cavalieri et le calcul infinitésimal créé par Newton (théorie des fluxions, 1669) et par Leibniz, sous sa forme plus moderne (1684). Ce Traité approfondit encore un peu le travail de Torricelli, dont il a la clarté d'expression. Mais déjà Wallis (analysis infinitorum 1654), Barrow (enseignant de Newton en 1661), Wren (fondateur de la Royal Society en 1660) sont sur la même voie et Gregory va revenir de Bologne (1664-1668).

La Géométrie des Indivisibles va céder la place à l'analyse. Mais l'ingéniosité combinatoire de ce Traité de la Roulette ravit.

Sommaire 1 Le Traité de la Roulette 2 Analyse du Traité, notations 3 Quadrature de la Roulette 4 L'art de décompter 4.1 la suite de Galilée et somme triangulaire 4.2 les sommes pyramidales 4.3 Les divisions égales, les ordres 5 Le décompte horizontal ou vertical: intégration par parties 6 Ce qui manque au Traité 7 Quelques intégrales du Traité de la Roulette 8 Conclusion(?) 9 Références 10 Voir aussi 11 Bibliographie

Le Traité de la Roulette

Le TR (Traité de la Roulette) comporte 18 propositions traitées en 6 +1 traités :

• 1/. Lettre de Mr Dettonville à Mr de Carcavi
• 2/. Traité des trilignes rectangles et de leurs onglets
• 3/. Propriétés des sommes simples
• 4/. Traité des sinus (du quart de cercle)
• 5/. Traité des arcs de cercle
• 6/. Petit traité des solides circulaires

• 7/. Traité général de la Roulette

Ils seront nommés (Ti), i = 1..7. Les 6 premiers permettent de faire les calculs (non faits par Pascal) qui serviront dans le (T7).

Les 18 propositions sont les neuf problèmes de Juin et les neuf d'Octobre :

Soit une demi-arche de roulette d'Arc OS (avec O(0 ; 0) ; S(Pi.a ; 2a)). H le point (Pi.a ; 0), qui forme donc le triligne rectangle.

L'aire OSH a été évaluée par Galilée (1592) (par pesée!) : 3/2 disques générateurs, enfin calculée par Roberval(1634) à l'aide de la fameuse "courbe auxiliaire" (y = sin x, dit en termes modernes); retrouvée par Torricelli ensuite (cf l'enquête très soignée de Jean Itard, du centre Koyré, sur l'antériorité de Roberval).

Pascal coupe la figure d'un trait horizontal, partant du point courant P, coupant le demi-cercle de diamètre SH en M, et le segment SH en Y, l'axe des ordonnées en Y'. Bien sûr, PM = arc MS, ce qui est la propriété caractéristique de la roulette.

Les 9 Propositions de Juin sont :

• Aire PYS; X & Y du barycentre de cette aire.

Faire tourner la figure autour de PY :

• Volume du solide engendré ; X & Y de son barycentre.

Faire tourner la figure autour de SY

• Volume du solide engendré ; X & Y de son barycentre.

Les 9 problèmes d'Octobre concernent une extension due à Wren (août 1658) :

• Rectification de l'arc MS ; X & Y de son barycentre.

Faire tourner l'arc MS autour de PY, d'un demi-tour :

• aire de la surface engendrée ; X & Y de son barycentre.

Faire tourner l'arc MS autour de SY, d'un demi-tour :

• aire de la surface engendrée ; X & Y de son barycentre.

Les Traités T1,2,4 sont novateurs. T3,6 reprennent Guldin(1637?). T5 explicite T4 via T2. Enfin, T7 articule le tout

Le Traité T2 est considéré par Émile Picard comme un chef-d'œuvre.

Analyse du Traité, notations

Notation : Elle sera faite selon essentiellement les références ci-dessous:

• C. pour Costabel et
• M. pour Merker.
• TR désignera : Traité de la Roulette.

On appellera somme des indivisibles : ß.

Quadrature de la Roulette

Voici la démonstration de la quadrature de la demi-roulette, en six lignes :

• Reprendre la figure précédente.

• Diviser SH en une infinité de parties égales "YY",

• et tracer les indivisibles, les segments YP = YM + MP.

• (Aucune difficulté à) Comprendre, avec Cavalieri, que ß YM = aire du demi-cercle : Pi.a²/2 (:= A1)

• Il reste ß MP = ß SM = ß (Pi.a - SM) = 1/2 ß Pi.a = 1/2 (Pi.a). ß = 1/2 Pi.a .(2a) = 2.A1

• L'aire de Roberval, que Galilée n'a pas su calculer, est donc 3.aire du demicercle.

FIN de démonstration.

Problème : doit-on écrire ß YM ou bien comme Torricelli et Pascal ß YM . YY, ce qui dans l'écriture de Leibniz deviendra : 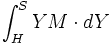? Nous respecterons ici le TR, en écrivant toujours les divisions égales YY et les segments (les indivisibles) partiront toujours de Y ; ceci afin de rester plus près du texte de Dettonville.

L'art de décompter

Pascal avait l'habitude de combiner jetons et bâtons, cela tout petit, raconte sa sœur.

On connaît le Triangle de Pascal. Et la combinatoire appliquée aux ars conjectandi.

Mais des faits plus élémentaires existent depuis longtemps (cf le livre de Conway et Guy).

la suite de Galilée et somme triangulaire

Soit un carreau carré. L'entourer à droite et par dessous de 3 carreaux de manière à former un carrelage carré de 4 carreaux. Entourer de 5 carreaux, on obtient un carrelage carré de 9 carreaux. Puis 7 carreaux de plus conduiront à 4^2 carreaux, et 9 à 5^2.

On reconnaît la somme des impairs [de 1 à 2t-1] = t^2 de Galilée, qui se démontre par récurrence : t^2 + gnomon (:= 2t + 1) = (t+1)^2.

Pascal connaissait certainement ce résultat, et celui qui s'en déduit : somme des entiers = n(n+1)/2.

mais il remarque plus : nommons les carrés par des lettres A, le deuxième gnomon B, etc.

La somme devient celle d'un tableau de "Poids" := P = A + 3 B + 5 C + 7 D +...

Il ne faut pas longtemps à Pascal pour découvrir qu'avec ce tableau symétrique, on peut écrire :

"Trace" de la diagonale := ß := (A + B + C + D + E)

Soit le tableau triangulaire supérieur, Y COMPRIS la diagonale, soit µ ; P = 2µ - ß.

Remarquer: µ = A + 2.B + 3.C + 4.D, c'est-à-dire le moment des poids alignés, par rapport à l'origine (1 est l'abscisse du carreau A) : c'est donc simplement le moment µ du levier d'Archimède.

Et par conséquent, µ/ß donne l'abscisse du "barycentre" :

C'est la fameuse règle "secrète", dont Archimède parle dans sa lettre à Dosithée. (Torricelli, Magiotti et Nardi, élèves de Castelli, ont en beaucoup discuté):

l'abscisse du barycentre est le barycentre des abscisses.

Pascal appelle cela, faire une somme triangulaire µ. On peut d'ailleurs décaler l'origine.

Pour s'exercer : appliquer au centre de gravité du quart de circonférence : .

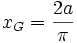Le barycentre du demi-disque s'en déduit : (2/3).{0 ; }.

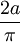Vérifier en appliquant le théorème de Guldin à la sphère et à la boule (énoncés de T4,T5 & T6).

On pourra aussi, en regardant la table de Pythagore avec le même gnomon, trouver que (ß n)² = ß n³ : c'est aussi un classique.

les sommes pyramidales

Tout enfant, avec des cubes, fait des pyramides ; Dettonville ne s'en est pas privé ! Soit l'axe Z vers le bas :

On place à la cote z= 1 le cube A, à la cote z=2, 4 cubes B à la cote z=3, 9 cubes C

On construit ainsi une belle pyramide.

(prendre des couleurs graduées en z produit un joli effet ; ce sont des objets bien connus en architecture, mais j'ai oublié leur nom : Pantènes ?)

Evidemment cette pyramide a comme plan de symétrie le plan x=y. L'ensemble des éléments de ce plan diagonal est cette fois, la somme moment µ (la dessiner pour s'en convaincre, sinon prendre des cubes!). Comme précédemment Dettonville prend la moitié de la pyramide, AVEC le plan de symétrie, et appelle cela la somme pyramidale (þ)

Dettonville obtient donc : 2 .(þ) - (µ) = 1².A + 2².B + 3².C + 4².D +5².E,

Pour comprendre Pascal, « il faut rester à manipuler ces cubes, jusqu'à en être convaincu ».

(Ceci est l'essence de ce qu'a voulu écrire Pascal : Voir & Conclure. D'ailleurs c'est le titre d'un de ses livres : l'esprit de géométrie et l'art de convaincre. Il y a là une "certaine" beauté esthétique, proche du style du "parfait" cathare, beauté sans doute pas étrangère au jansénisme de Pascal).

Application directe : prendre pour chiffre le numéro des lettres. En déduire à nouveau Σ n³.

Les divisions égales, les ordres

On ramasse les myrtilles avec un râteau d'environ 16 dents également espacées.

Soit 16 pailles de diamètre égal à la période spatiale du râteau.

Étaler les seize pailles côte à côte, et éventuellement avec une petite entretoise de guidage, les translater aisément en ratissant.

Cela est un moyen très VISUEL de calculer des aires, façon Dettonville.

Exemple : Découper un disque en carton. Avec celui-ci, dessiner une demi-arche de cycloïde. Y poser les pailles. Ratisser les pailles à gauche. Introduire le cercle directeur en carton selon SH. Ramener les pailles en ratissant à droite : la preuve expérimentale est faite : Aire = (aire du rectangle - aire du demi-cercle, A1), soit 3 A1. Après l'avoir montré, il FAUT le démontrer ; mais on est déjà convaincu. Quasiment tous les raisonnements de Dettonville se font à l'aide de ce peigne à myrtilles, qui existe déjà, sans le dire, chez Torricelli : les divisions sont égales sur les côtés du triligne rectangle. Mais aussi une exception : comme Torricelli, il se donne le droit de découper des arcs en longueurs égales, ce qui est plus subtil bien sûr, et exclut le peigne à myrtille.

Voilà donc que les indivisibles peuvent se diviser en 32 pailles de demi-diamètre, etc., jusqu'à 1024 (=2^10) minuscules pailles, etc. Il ne reste plus qu'à conclure, une fois cela VISUALISÉ : à la limite n tendant vers l'infini, pour 2^n apilles, il vient que l'aire sous la courbe A = f(1), B = f(2), C = f(3), c'est la somme ß := A+B+C+...

Mais Dettonville va plus loin :

Dans le calcul exact du Tableau carré de Galilée, il dit que le poids de la diagonale est NÉGLIGEABLE : donc 2µ - ß = 2µ ! le GRAND PAS VIENT d'être franchi : on négligera les termes de "ordre inférieur" : la somme des entiers quand n est très grand sera ~ n²/2

Dans le calcul exact de la Pyramide, le poids total sera 2þ - µ = 2þ ! Ainsi, la somme des cubes sera ~ n^4/4. La notion d'infini < infini² < infini³ dans les polynômes vient d'apparaître au grand jour. C'est la notion d'ORDRE de grandeur, bien plus importante que celle dont on philosophe sur les infinis de Pascal (mais très liée à la morale de Pascal). Le temps des paradoxes des indivisibles n'est pas encore terminé (il faudra un Darboux pour clore le débat!), mais les "bonnes" règles font surface.

Bien sûr, Dettonville n'écrira pas pour ses sommes doubles : ßß, et pour ses sommes triples : ßßß, mais il l'a VISUALISÉ. L'aurait-il symbolisé, il eût été le créateur du calculus, d'autant qu'il a compris l'intégration par parties :

Le décompte horizontal ou vertical: intégration par parties

Évidemment l'aire d'un triangle curviligne comme celui qui nous intéresse ici (la demi-roulette OSHO), on peut utiliser le principe des pailles aussi bien verticalement qu'horizontalement : l'aire ß PY .YY + ß PY' .Y'Y' = OS.SH,

mais ß PY. YY = ß PX . XX donc ß PX. XX = OS.OH - ß PY'.Y'Y'

Leibniz l'écrira plus tard : d(xy) = y .dx + x.dy. Pour l'heure, Dettonville ne fera que s'en servir, avec virtuosité.

Donc par rapport à Torricelli qui est le premier à parler en dimensions homogènes en ayant donné une dimension au "dx", Dettonville avance un pas de plus avec ses dx.dx.dx négligeables devant du X.dx.dx, X fini. Et avec ses sommes doubles ou triples et l'intégration par parties.

Ce qui manque au Traité

Le TR n'est pas un traité de calculus. Merker évoque :

• le caractère clos (du Cloître)
• l'impossibilité dans les calculs de somme double de prendre des divisions inégales.
• Wallis et Wren

• Le caractère clos : Dettonville montre bien le fait que somme de sinus(x) = sinus(x - Pi/2) ; donc on peut faire autant de somme de somme de somme... que l'on veut. C'est en quelque sorte la beauté du cercle qui aurait fasciné et confiné Pascal. Seul le T2 est un peu général ; mais néanmoins il reste axé sur ce problème de la cycloïde. D'autre part, lire le TR est un véritable jeu de piste, puisqu'on y donne juste "l'air de la démonstration".

Dans le seul calcul de somme simple, avec la touchante, qu'il utilise, soit ß(MY.MM), il indique nettement dans T2, qu'il suffit que les subdivisons soient indéfinies pour que arc et tangente (ou corde) se confondent. [Mais c'est Leibniz qui comprendra cette phrase comme : pour calculer la ß, il suffit de connaître la primitive. La relation tangente et somme de Barrow est retrouvée, mais surtout entre dérivée et primitive, cela solidement exprimé après des décennies de calculs cousins].Or, rien de tout cela n'existe dans le TR, limité à la seule remarque géométrique : , cela écrit en termes modernes. Mais JAMAIS Dettonville ne parle d'analyse. Il a voulu rester géomètre.

• Dettonville se limite aux arcs égaux: pourquoi ? Sans doute parce que l'esprit combinatoire reste DOMINANT : il préfère calculer comme Archimède ! Et, par ailleurs ses formules triangulaires (µ) et pyramidales (þ) ne sont valables qu'avec des divisions égales (M. p 52.57 et p114). Merker signale un paradoxe très joli, p131, sur les paradoxes de Tacquet, recensés par Gardies : on ne peut obtenir sans ruser la surface de la demi-sphère. Darboux relèvera lui aussi des paradoxes dans les aires de surfaces bien choisies.

• Pascal ne s'était pas enquis des travaux de Roberval (cf C.). Posant des questions auxquelles d'autres ont déjà répondu, il se met en porte-à-faux. D'où ses controverses avec Wallis (déjà très célèbre). Mais surtout quand Wren publie la rectification de la cycloïde en Août 1658, Pascal est pris de court : pour faire face, il va rédiger assez vite les problèmes d'Octobre. Mais ce n'est guère très glorieux. Certes, son œuvre (et surtout le T2) est admirable, mais Dettonville doit être, selon sa morale, assez amer d'avoir été doublé.

Inversement, Wallis a dû profiter de cette œuvre. Que doit Wallis au traité de Dettonville ? Beau sujet d'investigation.

Quelques intégrales du Traité de la Roulette

L'analyse M p50-85 est d'excellente didactique, pour tout amoureux de géométrie. Sont citées ici quelques intégrales (en notation modernes) qu'arrive à trouver Dettonville sans calcul différentiel a priori :

Exercice fondamental : Soit EE' la touchante en P se projetant en XX' : XX'.OP = EE'.PH [ dans nos notations : d(cosα = - (PH./OP).dα ]. C'est la seule fois où interviendra la touchante. Ensuite "tout est clos" car la dérivée seconde redonne l'opposée de la fonction [ Rappel : du temps de Pascal, la dérivée n'existe pas !]

Exercice 2 : Soit P1 et P2 se projetant en H1 et H2 : ß PH^n .PP = (ß HP^(n-1). HH) . R : 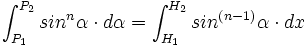, pour R= 1.

Exercice 3 : pour tout triligne rectangle, l'intégration par parties donne : .

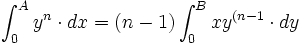mais aussi toutes sortes de formules monômes en x et y du type .

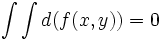Et Dettonville a bien remarqué géométriquement que du côté des intégrales curvilignes, cela "marchait" aussi. Et les propositions XII à XV du T2 deviennent des exploits de géométrie et de statique : par exemple calculer ß PY'².PP, soit 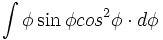, uniquement de manière géométrique. Mais il reste que ce type de méthode consistant à ramener une courbe, la roulette, à une succession de cercles sera inexploitable en analyse.

Conclusion(?)

En ce sens, cette belle tentative restera lettre morte. Néanmoins, n'oublions pas que Huygens va comprendre l'isochronisme de la cycloïde à ce moment: Pascal écrivant à Huygens n'est-il pas le catalyseur, comme Wren a été le catalyseur des problèmes d'Octobre?

Et Newton, remarquable géomètre-dynamicien, s'il en fût, n'est-il pas Pascalien sans le savoir, en renonçant au calcul différentiel pour écrire les Principia (cf Principia et Calculus ).

Références

• Pascal, œuvres complètes, J.Chevalier, ed la Pléïade
• Pascal, œuvres complètes, J. Mesnard, ed Desclée de Brouwer
• Pascal, Pensées, ed Flammarion 1976
• Roberval, traité des indivisibles, U Paris VII, 1987
• Fermat, Œuvres, par Tannery, ed Gauthier-Villars, 1891-1922
• Leibniz, calcul différentiel, ed Vrin, 1989

• Costabel, les secrets de la roulette, Rev Hist Sc, 15,(1962)
• Cederom, PU Clermont-Ferrand, 1999, par Descotes & Proust : Lettres de Dettonville.
• DeGandt, la géométrie des indivisibles, APMEP, fragments d'histoire des math II, 65,(1987)
• Merker, le chant du cygne des indivisibles,PUFC,(2001),ISBN 2-84627-038-4
• Gardies, Pascal entre Eudoxe et Cantor, 1984, ed Vrin.

Voir aussi

• Blaise Pascal
• Méthode des indivisibles
• Cycloïde
• Roberval
• Huygens
• Isaac Newton
• Gottfried Wilhelm von Leibniz

Bibliographie

• Pascal, Œuvres complètes, J.Chevalier, ed la Pléïade.