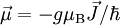Paramagnétisme de langevin

Le paramagnétisme désigne en magnétisme le comportement d'un milieu matériel qui ne possède pas d'aimantation spontanée mais qui, sous l'effet d'un champ magnétique extérieur, acquiert une aimantation dirigée dans le même sens que ce champ d'excitation. Un matériau paramagnétique possède donc une susceptibilité magnétique de valeur positive (contrairement aux matériaux diamagnétiques), en général assez faible. Cette aimantation disparaît lorsque le champ d'excitation est coupé, il n'y a donc pas de phénomène d'hysteresis comme pour le ferromagnétisme.

Le paramagnétisme ne désigne pas une propriété intrinsèque d'un matériau mais un comportement en réponse à un champ magnétique, comportement qui peut changer selon les conditions considérées. Ainsi, un matériau ferromagnétique devient paramagnétique quand sa température dépasse sa température de Curie. Il peut également devenir paramagnétique pour des échantillons de taille suffisamment petite : on parle alors de superparamagnétisme.

À l'échelle microscopique, on peut modéliser un matériau paramagnétique par un ensemble de dipôles magnétiques indépendants. La réponse du système à un champ magnétique appliqué est alors déterminée par le rapport de forces entre l'énergie magnétique d'une part qui tend à ordonner les dipôles en les alignant selon le champ appliqué, et l'énergie d'agitation thermique d'autre part qui favorise le désordre. Le traitement de ce problème par la physique statistique permet de démontrer la loi de Curie qui affirme que la susceptibilité magnétique d'un matériau paramagnétique est inversement proportionnelle à la température.

Sommaire 1 Aspect microscopique 2 Aspect macroscopique 2.1 Régime linéaire 2.2 Régime saturé 3 Paramagnétisme de Langevin 4 Moment magnétique des électrons de conduction : paramagnétisme de Pauli 5 Matériaux paramagnétiques 6 Notes et références 7 Voir aussi 8 Bibliographie 9 Liens externes

Aspect microscopique

Le moment magnétique d'un atome 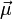est relié à son moment cinétique 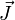par :

avec g le facteur de Landé et μ_B le magnéton de Bohr

Le moment cinétique total résulte de 3 composantes :

• Spin
• Moment cinétique orbital des électrons
• Spin nucléaire des nucléons.

Le spin nucléaire étant très faible, il n'apporte pas de contribution suffisante à la susceptibilité pour être pris en compte. Il est cependant possible de le mesurer, et il est utilisé en médecine par l'imagerie par résonance magnétique

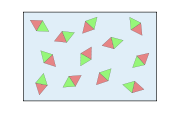
En l'absence de champ magnétique externe, le moment magnétique de chaque atome est orienté au hasard, et la somme de ces moments magnétiques (micro-aimants) est donc nulle à l'échelle macroscopique, le corps n'est pas aimanté.

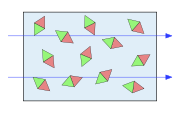
En présence d'un champ magnétique externe, chaque moment magnétique d'atome 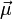tend à s'aligner dans la même direction et le même sens que le champ magnétique externe, et on observe une précession de ce moment magnétique.

Dans les matériaux paramagnétiques, les moments magnétiques de spin dominent sur ceux produits par les mouvements orbitaux des électrons.

Aspect macroscopique

Régime linéaire

Pour la plupart des matériaux dits paramagnétiques et sous des conditions raisonnables de température et de champ magnétique extérieur, l'aimantation 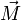du paramagnet est proportionnelle au champ appliqué  :

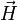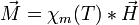avec χ_m(T) > 0 qui dépend de la température selon la loi de Curie.

L'aimantation décroit avec température car celle-ci est le reflet macroscopique de l'agitation thermique des atomes. À noter que χ_m est en toute rigueur une matrice 3*3 mais se réduit dans la majorité des cas à un nombre scalaire dans le cas des matériaux lhi (linéaire, homogène et isotrope).

Régime saturé

Si le champ d'excitation augmente, 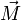ne reste plus proportionnel à 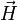et tend vers une constante 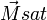quel que soit 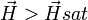, on parle alors de saturation.

Ce régime n'est pas observable à température ambiante car la susceptibilité magnétique y étant trop faible, il faudrait un 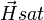de 1000 Tesla pour que la saturation du matériau ait lieu. Le régime est alors essentiellement linéaire.

Ce régime est observable aux basses températures, de l'ordre de quelques Kelvin, à partir de champs de 0,5 à 1 Tesla^[1].

Paramagnétisme de Langevin

Paul Langevin a introduit l'idée selon laquelle le moment magnétique d'un corps peut être la somme des moments magnétiques de chaque atome. Toutefois, une augmentation de la température apporte de l'agitation thermique qui entraîne la désorientation des moments magnétiques des atomes, malgré l'influence du champ magnétique extérieur. Paul Langevin explique alors la diminution du paramagnétisme comme une fonction inversement proportionnelle à la température. Ce phénomène est décrit par la loi de Curie :

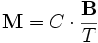
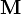est la magnétisation

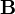est le flux du champ magnétique appliqué, mesuré en teslas

T est la température absolue, en kelvins

C est la constante de Curie du matériau. Elle est définie par :

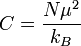
où N est le nombre de moments magnétiques à considérer, μ est un moment magnétique individuel et k_B est la constante de Boltzmann.

Moment magnétique des électrons de conduction : paramagnétisme de Pauli

Dans un métal les électrons de conduction peuvent se déplacer presque librement, ils sont très faiblement liées aux atomes du métal (par exemple Modèle de Drude). Comme les électrons possèdent un moment magnétique de spin, on attend alors un apport à la susceptibilité, qui est similaire à la loi de Curie. Les électons étant des fermions, ils doivent alors vérifier le principe de Pauli, et on observe la loi suivante :

,

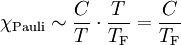où T_F est une constante du matériaux.

Pour être plus précis, on peut démontrer qu'il existe une dépendance de la force du champ magnétique.

Matériaux paramagnétiques

• Aluminium Al [13] (métal)
• Baryum Ba [56] (métal alcalino-terreux)
• Calcium Ca [20] (métal alcalino-terreux)
• Oxygène liquide O₂ [8] (non métallique)
• Platine Pt [78] (métal de transition)
• Sodium Na [11] (métal alcalin)
• Strontium Sr [38] (métal alcalino-terreux)
• Uranium U [92] (métal (actinide))
• Magnésium Mg [12] (métal alcalino-terreux)
• Fer γ (austénite) Fe [26]

• Technétium Tc [43] (métal de transition artificiel)
• Lithium Li [3] (métal alcalin)

Notes et références

Voir aussi

• Magnétisme
• Ferromagnétisme
• Diamagnétisme
• Dipôle magnétique
• Monopôle magnétique
• Résonance paramagnétique électronique

Bibliographie

• Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l’état solide [« Solid state physics »], 1998 [détail des éditions] 
• L. P. Lévy, Magnétisme et Supraconductivité (EDP Sciences)
• Lev Landau et Evguéni Lifchitz, Physique théorique, tome 8 : Électrodynamique des milieux continus, éd. MIR, Moscou [détail des éditions]
• Neil W. Ashcroft, N. David Mermin, Physique des solides [détail des éditions]
• John David Jackson, Électrodynamique classique [« trad. de (en)Classical Electrodynamics »] 

Liens externes

• Classification of Magnetic Materials by Applied Alloy Chemistry Group at University of Birmingham.

Électromagnétisme • Électricité • Électronique • Électrotechnique • Électrochimie • Automatique • Traitement du signal
Électrostatique : Champ électrique • Charge électrique • Loi de Coulomb • Potentiel électrique
Magnétostatique : Champ magnétique • Moment magnétique • Loi de Biot et Savart
Électrocinétique : Champ électromagnétique • Courant de déplacement • Courant électrique • Ampère • Équations de Maxwell • Force électromotrice • Force de Lorentz • Induction électromagnétique • Loi de Lenz-Faraday • Rayonnement électromagnétique
Magnétisme : Diamagnétisme • Paramagnétisme • Superparamagnétisme • Ferromagnétisme • Antiferromagnétisme • Ferrimagnétisme • Loi de Curie • Domaine de Weiss • Susceptibilité magnétique • Perméabilité magnétique

• Portail de la physique