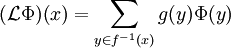Operateur de transfert

En mathématiques, l'opérateur de transfert encode l'information d'une application itérée et est fréquemment utilisé pour étudier le comportement des systèmes dynamiques, de la mécanique statistique, du chaos quantique et des fractals. L'opérateur de transfert est quelquefois appelé l'opérateur de Ruelle, en l'honneur de David Ruelle, ou l'opérateur de Ruelle-Perron-Frobenius faisant référence à l'applicabilité du théorème de Frobenius-Perron pour la détermination des valeurs propres de l'opérateur.

La fonction itérée étudiée est une application 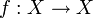d'un ensemble arbitraire X. L'opérateur de transfert est défini comme un opérateur 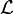agissant sur l'espace des fonctions 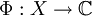comme

où 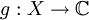est une valuation de fonction auxiliaire. Lorsque f possède un déterminant jacobien, alors g est généralement pris pour .

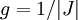Certaines questions à propos de la forme et la nature de l'opérateur de transfert sont étudiées dans la théorie des opérateurs de composition.

Applications

Considérant que l'itération d'une fonction f conduit naturellement à l'étude des orbites des points de X sous l'itération (l'étude des systèmes dynamiques), l'opérateur de transfert définit comment les applications (continues) évoluent sous l'itération. Ainsi, les opérateurs de transfert apparaissent fréquemment dans les problèmes de physique, tels que le chaos quantique et la mécanique statistique, où l'attention est concentrée sur l'évolution temporelle des fonctions continues.

Le cas est fréquent où l'opérateur de transfert est positif, possède des valeurs propres discrètes, positives, ayant des valeurs réelles, avec la plus grande valeur propre étant égale à un. Pour cette raison, l'opérateur de transfert est quelquefois appelé l'opérateur de Frobenius-Perron.

Les valeurs propres de l'opérateur de transfert sont habituellement des fractals. Lorsque le logarithme de l'opérateur de transfert correspond au Hamiltonien quantique, les valeurs propres seront typiquement très étroitement alignées, et ainsi, même un ensemble sélectionné attentivement d'états quantiques sera entouré d'un grand nombre d'états propres fractals très différent avec un support différent de zéro sur le volume entier. Ceci peut être utilisé pour expliquer beaucoup de résultats issus de la mécanique statistique classique, incluant l'irréversabilité du temps ainsi que l'augmentation de l'entropie.

L'opérateur de transfert de l'application de Bernoulli 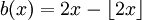est résolvable exactement et est un exemple classique de chaos déterministe; les valeurs propres discrètes correspondent aux polynômes de Bernoulli. Cet opérateur possède aussi un spectre continu constituant la fonction zeta d'Hurwitz.

L'opérateur de transfert de l'application de Gauss 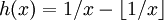est appelé l'opérateur de Gauss-Kuzmin-Wirsing (GKW) et en raison de son extraordinaire difficulté, n'a pas encore été pleinement résolu. La théorie de l'opérateur GKW remonte à l'hypothèse faite par Gauss sur les fractions continues et est reliée fermement à la fonction zeta de Riemann.

Voir aussi

• schéma de Bernoulli

Références

• David Ruelle, Thermodynamic formalism: the mathematical structures of classical equilibrium statistical mechanics

• Dieter H. Mayer, The Ruelle-Araki transfer operator in classical statistical mechanics

• David Ruelle, Dynamical Zeta Functions and Transfer Operators, (2002) Institut des Hautes Etudes Scientifiques preprint IHES/M/02/66. (Provides an introductory survey).