Normale à une surface

Normale à une surface
Un plan et deux vecteurs normaux.

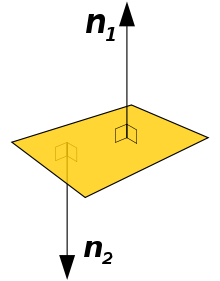
En géométrie, la droite normale à une surface en un point est la droite orthogonale au plan tangent en ce point. Les vecteurs directeurs de cette droite sont appelés vecteurs normaux à la surface.

Une convention fréquente pour les surfaces fermées est de particulariser un vecteur normal unitaire, vecteur de norme 1 et orienté vers l'extérieur.

Plus généralement, il est possible de considérer les vecteurs normaux à une hypersurface dans un espace euclidien, voire dans une variété riemannienne.

Sommaire

Exemple : le plan en dimension 3

Dans un espace euclidien de dimension trois, on peut l'obtenir simplement par le produit vectoriel de deux vecteurs directeurs du plan. Soit un plan défini par le point A(a_1;a_2;a_3)\, et les vecteurs \vec u = \begin{bmatrix}u_1\\ u_2\\ u_3\end{bmatrix} et \vec v = \begin{bmatrix}v_1\\ v_2\\ v_3\end{bmatrix}. Son système d'équations paramétriques est :

\begin{cases} x = a_1 + \lambda u_1 + \mu v_1 \\ y = a_2 + \lambda u_2 + \mu v_2 \\ z = a_3 + \lambda u_3 + \mu v_3\end{cases}

Soit \vec w = \vec u \times \vec v le vecteur résultat du produit vectoriel. Le vecteur normal au plan est :

\vec n = \frac{\vec w}{\|\vec w\|} ou \vec n = -\frac{\vec w}{\|\vec w\|}

Si le plan est défini par son équation cartésienne :

Ax + By + Cz + D = 0

Son vecteur normal est :

\vec n = \begin{bmatrix}A\\B\\C\end{bmatrix}

et son vecteur normal unitaire est :

\vec n = \frac{1}{\sqrt{A^2+B^2+C^2}} \cdot \begin{bmatrix}A\\B\\C\end{bmatrix}

Vecteur normal en un point régulier

Soit une surface définie par un paramétrage

M(u,v)=\bigl(x(u,v),y(u,v),z(u,v)\bigr)

avec des fonctions x,y,z de classe C1. Le point de paramètre (u,v) est dit régulier lorsque les vecteurs dérivés partiels en ce point sont indépendants. On peut alors former leur produit vectoriel

N(u,v)=\frac{\partial M}{\partial u}(u,v) \wedge \frac{\partial M}{\partial v}(u,v)

qui constitue un vecteur normal à la surface (non nécessairement unitaire).

Lien avec le gradient

Si la surface est donnée par une équation cartésienne f(x,y,z)=0, avec une fonction f de classe C1, un point de la surface est dit régulier si le gradient de f est non nul en ce point. C'est alors le vecteur gradient lui-même qui constitue un vecteur normal.

La démonstration formelle de ce résultat fait intervenir le théorème des fonctions implicites. Il est toutefois possible d'en donner une approche simplifiée à l'aide de la notion de "variations infinitésimales".

En effet, si on se place en un point M(x,y,z) de la surface, sur son voisinage, la fonction f garde toujours la même valeur : 0. Par conséquent, sa variation infinitésimale lors d'un déplacement sur la surface défini par le vecteur \vec{dl} = (dx, dy, dz) est nulle : df = 0.

Or, par définition du gradient, on a df = \vec{grad(f)}.\vec{dl}. Puisque ce produit scalaire est nul, le gradient en M est bien perpendiculaire à la surface en ce point.

Champ de normales

Un champ de normales (normales en plusieurs points) à une forme permet de retrouver sa surface tridimensionnelle, en passant par une étape d'intégration de ce champ.

Voir aussi

Liens internes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Normale à une surface de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Normale a une surface — Normale à une surface Un plan et deux vecteurs normaux. En géométrie, la droite normale à une surface en un point est la droite orthogonale au plan tangent en ce point. Les vecteurs directeurs de cette droite sont appelés vecteurs normaux à la… …   Wikipédia en Français

  • Courbe tracée sur une surface — Une courbe tracée sur une surface Σ est une application différentiable d image c(I) contenue dans Σ. Exemples remarquables Sur la sphère unité de R3, un grand cercle est la trace sur S2 …   Wikipédia en Français

  • normale — ● normale nom féminin Ce qui est normal, courant, la moyenne : Une intelligence supérieure à la normale. Situation habituelle : Retour à la normale. Familier. École normale (sans article et avec majuscule). Météorologie Moyenne d un élément… …   Encyclopédie Universelle

  • Courbe Tracée Sur Une Surface — Une courbe tracée sur une surface Σ est une application différentiable d image c(I) contenue dans Σ. Exemples remarquables Sur la sphère unité de R3, un grand cercle est la trace sur S …   Wikipédia en Français

  • Courbe tracee sur une surface — Courbe tracée sur une surface Une courbe tracée sur une surface Σ est une application différentiable d image c(I) contenue dans Σ. Exemples remarquables Sur la sphère unité de R3, un grand cercle est la trace sur S …   Wikipédia en Français

  • Normale — Normal Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • surface — [ syrfas ] n. f. • 1611; superface 1521; lat. superficies → superficie; de sur et face 1 ♦ Partie extérieure (d un corps), qui le limite en tous sens. ⇒ face. La surface de la Terre, la surface terrestre. À la surface du sol. « une surface pure… …   Encyclopédie Universelle

  • Surface d'egale pente — Surface d égale pente Dans la famille des surfaces paramétrées et orientées de R3, une surface d égale pente α s appuyant sur une courbe plane c tracée sur le plan horizontal {z = 0} est l enveloppe des plans tangents à la courbe c dont la… …   Wikipédia en Français

  • Surface d'onde — ● Surface d onde ensemble des points où une composante spécifiée d une onde périodique a la même phase au même instant. (La normale à la surface d onde en un point est la direction de propagation.) …   Encyclopédie Universelle

  • Surface de niveau — Verticale et surface de niveau Verticale et surfaces de niveau mettent en évidence les dénivellations affectant un territoire géographique lorsqu il est représenté sur un plan. La verticale d un point de la surface est une ligne imaginaire… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”