Nombre de wieferich

Nombre de wieferich

Nombre de Wieferich

En mathématiques, un nombre premier de Wieferich est un nombre premier p tel que 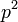p^2\, divise 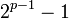2^{p-1} - 1\,, comparer ceci avec le petit théorème de Fermat, qui énonce que chaque nombre premier p divise 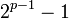2^{p - 1} - 1\,. Les nombres premiers de Wieferich furent décrits en premier par Arthur Wieferich en 1909 dans ses travaux relatifs au dernier théorème de Fermat.

Sommaire

La recherche des nombres premiers de Wieferich

Les seuls nombres premiers de Wieferich connus sont 1093 et 3511 (Encyclopédie électronique des suites entières (id=A001220), trouvés par W. Meissner en 1913 et N. G. W. H. Beeger en 1922, respectivement ; si d'autres existent, ils doivent être 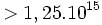> 1,25.10^{15}\, [1]. Il a été conjecturé qu'il n'existe qu'un nombre fini de nombres premiers de Wieferich ; la conjecture est restée non démontrée jusqu'à aujourd'hui, bien que J. H. Silverman fut capable de montrer en 1988 que si la conjecture abc est valable, alors pour tout nombre entier positif a > 1, il existe une infinité de nombres premiers p tel que 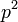p^2\, ne divise pas a^{p-1} - 1\,.

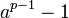Propriétés des nombres premiers de Wieferich

Il peut être montré qu'un facteur premier p d'un nombre de Mersenne 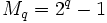M_q = 2^q - 1\, est un nombre premier de Wieferich ssi 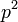p^2\, divise 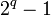2^q - 1\,  ; à partir de ceci, il suit immédiatement qu'un nombre premier de Mersenne ne peut pas être un nombre premier de Wieferich. Aussi, si p est un nombre premier de Wieferich, alors 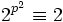2^{p^2} \equiv 2\, mod p^2\,.

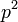Les nombres premiers de Wieferich et le dernier théorème de Fermat

Le théorème suivant connectant les nombres premiers de Wieferich et le dernier théorème de Fermat fut prouvé par Wieferich en 1909 :

Soit p un nombre premier, et soient x, y, z des nombres naturels tels que 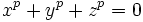x^p + y^p + z^p = 0\,. De plus, supposons que p ne divise pas le produit xyz. Alors p est un nombre premier de Wieferich.

En 1910, Mirimanoff fut capable de développer le théorème en montrant que, si les prérequis du théorème reste valable pour un certain nombre premier p, alors p doit aussi diviser 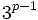3^{p-1}\,. Les nombres premiers de cette sorte ont été appelés les nombres premiers de Mirimanoff à l'occasion, mais le nom ne fut pas d'usage mathématique général.

Voir aussi

Lien externe


Lectures pour aller plus loin

  • A. Wieferich, "Zum letzten Fermat'schen Theorem", Journal für Reine Angewandte Math., 136 (1909) 293-302
  • N. G. W. H. Beeger, "On a new case of the congruence 2p − 1 = 1 (p2), Messenger of Math, 51 (1922), 149-150
  • W. Meissner, "Über die Teilbarkeit von 2pp − 2 durch das Quadrat der Primzahl p=1093, Sitzungsber. Akad. d. Wiss. Berlin (1913), 663-667
  • J. H. Silverman, "Wieferich's criterion and the abc-conjecture", Journal of Number Theory, 30:2 (1988) 226-237
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre de Wieferich ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre de wieferich de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Nombre De Wieferich — En mathématiques, un nombre premier de Wieferich est un nombre premier p tel que divise , comparer ceci avec le petit théorème de Fermat, qui énonce que chaque nombre premier p divise . Les nombres premiers de Wieferich furent décrits en premier… …   Wikipédia en Français

  • Nombre de Wieferich — En mathématiques, un nombre premier de Wieferich est un nombre premier p tel que divise , comparer ceci avec le petit théorème de Fermat, qui énonce que chaque nombre premier p divise . Les nombres premiers de Wieferich furent décrits en premier… …   Wikipédia en Français

  • Nombre de Poulet — Nombre et supernombre de Poulet Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe… …   Wikipédia en Français

  • Nombre De Wall-Sun-Sun — En mathématiques, un nombre premier de Wall Sun Sun est une certaine catégorie de nombre premier. Un nombre premier p > 5 est appelé un nombre premier de Wall Sun Sun si p2 divise , où F(n) est le n ième nombre de Fibonacci et est le symbole… …   Wikipédia en Français

  • Nombre De Wilson — En mathématiques, un nombre premier de Wilson est une certaine catégorie de nombre premier. Un nombre premier p est appelé un nombre premier de Wilson si divise , où ! désigne la fonction factorielle ; comparer ceci avec le théorème de… …   Wikipédia en Français

  • Nombre de wall-sun-sun — En mathématiques, un nombre premier de Wall Sun Sun est une certaine catégorie de nombre premier. Un nombre premier p > 5 est appelé un nombre premier de Wall Sun Sun si p2 divise , où F(n) est le n ième nombre de Fibonacci et est le symbole… …   Wikipédia en Français

  • Nombre de wilson — En mathématiques, un nombre premier de Wilson est une certaine catégorie de nombre premier. Un nombre premier p est appelé un nombre premier de Wilson si divise , où ! désigne la fonction factorielle ; comparer ceci avec le théorème de… …   Wikipédia en Français

  • Nombre De Wolstenholme — En mathématiques, un nombre premier de Wolstenholme est une certaine catégorie de nombres premiers. Un nombre premier p est appelé nombre premier de Wolstenholme ssi la condition suivante reste valable : Les nombres premiers de Wolstenholme… …   Wikipédia en Français

  • Nombre de wolstenholme — En mathématiques, un nombre premier de Wolstenholme est une certaine catégorie de nombres premiers. Un nombre premier p est appelé nombre premier de Wolstenholme ssi la condition suivante reste valable : Les nombres premiers de Wolstenholme… …   Wikipédia en Français

  • Nombre et supernombre de Poulet — Un test de primalité courant pour un nombre impair n consiste à tester si n divise 2 n 2 : dans le cas contraire, en vertu du petit théorème de Fermat, on conclut que n n est pas premier. Cependant il existe des nombres composés qui passent… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”