Nombre Premier Palindrome

Nombre Premier Palindrome

Nombre premier palindrome

Page d'aide sur l'homonymie Pour les articles homonymes, voir Palindrome (homonymie).

En mathématiques, un nombre premier palindrome est un nombre premier qui est aussi un nombre palindrome. Le caractère palindrome dépend de la base du système de numération et de ses conventions d'écriture, tandis que la primalité est indépendante de ce genre de considérations.

Les premiers nombres premiers palindromes en base 10 sont:

2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301, 10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741, 15451, 15551, 16061, 16361, 16561, 16661, 17471, 17971, 18181, 18481, 19391, 19891, 19991

Il peut être noté dans liste ci-dessus, qu'il n'existe pas de nombres premiers palindromes à 2 ou 4 chiffres, excepté pour 11. Si l'on considère le test de divisibilité pour 11, il peut être déduit que tout nombre palindrome avec un nombre pair de chiffres est divisible par 11.

On ignore s'il existe une infinité de nombres premiers palindromes en base 10. Le plus grand nombre premier palindrome connu est 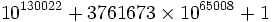10^{130022} + 3761673 \times 10^{65008} + 1\,, qui fut découvert par Harvey Dubner le 7 novembre 2004 et annoncé le 19 novembre 2004.

En binaire, les nombres premiers palindromes les plus faciles à obtenir sont les nombres premiers de Mersenne, puisqu'ils sont aussi des nombres premiers uniformes. Les quatre premiers nombres premiers palindromes (qui ne sont pas nombres de Mersenne) sont 5 (101), 17 (10001), 73 (1001001) et 107 (1101011).

Ribenboim définit un nombre premier triplement palindrome comme un nombre qui, en plus d'être un nombre premier palindrome, possède un nombre de chiffres qui est lui-même un nombre premier palindrome. Par exemple, 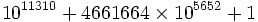10^{11310} + 4661664 \times 10^{5652} + 1\,, possède 11311 chiffres. Il est possible qu'un nombre premier triplement palindrome en base 10 puisse être aussi palindrome dans une autre base, telle que la base 2, mais il serait hautement remarquable s'il était aussi triplement palindrome dans cette base.

Références

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre premier palindrome ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Premier Palindrome de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Nombre premier palindrome — Pour les articles homonymes, voir Palindrome (homonymie). En mathématiques, un nombre premier palindrome est un nombre premier qui est aussi un nombre palindrome. Le caractère palindrome dépend de la base du système de numération et de ses… …   Wikipédia en Français

  • Nombre Palindrome — Pour les articles homonymes, voir Palindrome (homonymie). Un nombre palindrome est un nombre symétrique écrit dans une certaine base a comme ceci : . Tous les nombres en base 10 d un chiffre {0, 1, 2, 3, 4, 5 …   Wikipédia en Français

  • Nombre palindrome — Pour les articles homonymes, voir Palindrome (homonymie). Un nombre palindrome est un nombre symétrique écrit dans une certaine base a comme ceci : . Tous les nombres en base 10 d un chiffre {0, 1, 2, 3, 4, 5, 6, 7 …   Wikipédia en Français

  • Nombre Polydivisible — En mathématiques, un nombre polydivisible est un entier naturel s écrivant avec les chiffres qui possède les propriétés suivantes : Son premier chiffre n est pas 0. Le nombre formé par ses deux premiers chiffres est un multiple de 2. Le… …   Wikipédia en Français

  • Nombre polydivisible — En mathématiques, un nombre polydivisible est un entier naturel s écrivant avec les chiffres qui possède les propriétés suivantes : Son premier chiffre n est pas 0. Le nombre formé par ses deux premiers chiffres est un multiple de 2. Le… …   Wikipédia en Français

  • 300 (nombre) — Nombres 300 à 399 Cet article recense les nombres qui ont des propriétés remarquables allant de trois cents (300) à trois cent quatre vingt dix neuf (399). Sommaire : 300 · 301 · 302 · 303 · 304 · 305 · 306 · 307 · 308 · 309 310 · 311 · 312… …   Wikipédia en Français

  • 300 à 399 (nombre) — Nombres 300 à 399 Cet article recense les nombres qui ont des propriétés remarquables allant de trois cents (300) à trois cent quatre vingt dix neuf (399). Sommaire : 300 · 301 · 302 · 303 · 304 · 305 · 306 · 307 · 308 · 309 310 · 311 · 312… …   Wikipédia en Français

  • 301 (Nombre) — Nombres 300 à 399 Cet article recense les nombres qui ont des propriétés remarquables allant de trois cents (300) à trois cent quatre vingt dix neuf (399). Sommaire : 300 · 301 · 302 · 303 · 304 · 305 · 306 · 307 · 308 · 309 310 · 311 · 312… …   Wikipédia en Français

  • 301 (nombre) — Nombres 300 à 399 Cet article recense les nombres qui ont des propriétés remarquables allant de trois cents (300) à trois cent quatre vingt dix neuf (399). Sommaire : 300 · 301 · 302 · 303 · 304 · 305 · 306 · 307 · 308 · 309 310 · 311 · 312… …   Wikipédia en Français

  • 302 (nombre) — Nombres 300 à 399 Cet article recense les nombres qui ont des propriétés remarquables allant de trois cents (300) à trois cent quatre vingt dix neuf (399). Sommaire : 300 · 301 · 302 · 303 · 304 · 305 · 306 · 307 · 308 · 309 310 · 311 · 312… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”