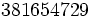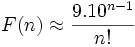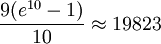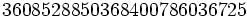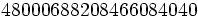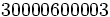Nombre Polydivisible

En mathématiques, un nombre polydivisible est un entier naturel s'écrivant avec les chiffres 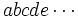qui possède les propriétés suivantes :

1. Son premier chiffre n'est pas 0.
2. Le nombre formé par ses deux premiers chiffres 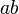est un multiple de 2.
3. Le nombre formé par ses trois premiers chiffres 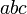est un multiple de 3.
4. Le nombre formé par ses quatre premiers chiffres 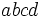est un multiple de 4.
5. etc.

Par exemple, 345654 est un nombre polydivisble à six chiffres, mais 123456 ne l'est pas, parce que 1234 n'est pas un multiple de 4. Les nombres polydivisibles peuvent être définis dans n'importe quelle base. Nonobstant, les nombres dans cet article sont tous en base 10, ainsi, les chiffres de 0 à 9 sont permis.

Sommaire 1 Arrière-plan 2 Combien de nombres polydivisibles existent ? 3 Compter les nombres polydivisibles 4 Problèmes connexes 5 Lien externe

Arrière-plan

Les nombres polydivisibles sont une généralisation du problème suivant très connu de mathématiques récréatives :

Arranger les chiffres de 1 à 9 dans un ordre où les deux premiers chiffres forment un multiple de 2, les trois premiers chiffres forment un multiple de 3, les quatre premiers chiffres forment un multiple de 4 etc. et finalement, le nombre entier est un multiple de 9.

La solution du problème est un nombre polydivisible à neuf chiffres avec la condition additionnelle qu'il contienne les chiffres de 1 à 9 exactement une fois chacun. Il existe 2 492 nombres polydivisibles à neuf chiffres, mais le seul qui satisfasse à la condition additionnelle est

Combien de nombres polydivisibles existent ?

Si k est un nombre polydivisible avec n-1 chiffres, alors il peut être étendu pour créer un nombre polydivisble avec n chiffres s'il existe un nombre compris entre 10k et 10k+9 qui est divisible par n. Si n est inférieur ou égal à 10, alors il est toujours possible d'étendre un nombre polydivisible à n-1 chiffres en un nombre polydivisible à n chiffres de cette manière, et il peut exister plus qu'une extension possible. Si n est plus grand que 10, il n'est pas toujours possible d'étendre un nombre polydivisble de cette manière, et lorsque n devient plus grand, les chances de pouvoir étendre un nombre polydivisble donné deviennent plus petites.

En moyenne, chaque nombre polydivisble de n-1 chiffres peut être étendu à un nombre polydivisble de n chiffre de 10/n manières différentes. Ceci conduit à l'estimation suivante du nombre de nombres polydivisibles de n chiffres, que nous noterons F(n) :

En sommant toutes les valeurs de n, cette estimation suggère que le nombre total de nombres polydivisibles sera approximativement

En fait, cette approximation approche le nombre actuel de nombres polydivisible de 3 %.

Compter les nombres polydivisibles

Nous pouvons trouver les valeurs actuelles de F(n) en comptant le nombre de nombres polydivisbles d'une longueur donnée :

Longueur n	F(n)	Estimation de F(n)		Longueur n	F(n)	Estimation de F(n)		Longueur n	F(n)	Estimation de F(n)
1	9	9		11	2225	2255		21	18	17
2	45	45		12	2041	1879		22	12	8
3	150	150		13	1575	1445		23	6	3
4	375	375		14	1132	1032		24	3	1
5	750	750		15	770	688		25	1	1
6	1200	1250		16	571	430
7	1713	1786		17	335	253
8	2227	2232		18	180	141
9	2492	2480		19	90	74
10	2492	2480		20	44	37

Il existe 20 456 nombres polydivisibles tous ensembles, et le plus long nombre polydivisible, qui possède 25 chiffres, est :

Problèmes connexes

D'autres problèmes impliquent les nombres polydivisibles :

• Trouver des nombres polydivisibles avec des restrictions supplémentaires sur les chiffres - par exemple, le nombre polydivisible le plus long qui ne contient que des chiffres pairs est :

• Trouver les nombres palindromes polydivisibles - par exemple, le nombre polydivisible palindrome le plus long est

• Énumérer les nombres polydivisibles dans les autres bases.

Lien externe

• Le problème des neuf chiffres et sa solution

• Portail des mathématiques