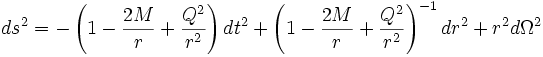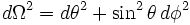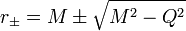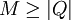Métrique de Reissner-Nordström

En astrophysique, un trou noir de Reissner-Nordström est un trou noir qui possède une masse M, une charge électrique non-nulle Q, et pas de moment angulaire (i.e. un trou noir chargé, mais sans rotation). Puisque la répulsion électromagnétique d'une masse chargée, lors de la compression durant la formation du trou noir, est très largement supérieure à l'attraction gravitationnelle (par environ 40 ordres de grandeur), on pense qu'il s'est formé très peu de ces trous noirs.

Sommaire 1 Description 2 Trou noir et supersymétrie 3 Généralisation 4 Références 5 Lien externe

Description

Les solutions de l'équation d'Einstein pour le cas d'une masse ponctuelle chargée électriquement et sans rotation dans un espace vide ont été obtenues en 1918 par Hans Reissner et Gunnar Nordström, peu de temps après que Karl Schwarzschild ait trouvé la métrique qui porte son nom et qui décrit les solutions pour une masse ponctuelle sans rotation et sans charge électrique.

La métrique de Reissner-Nordström généralise celle de Schwarzschild et s'écrit :

où les unités géométriques ont été utilisées, c'est-à-dire que la vitesse de la lumière, la constante gravitationnelle et la constante de Coulomb sont égales à 1 (c = G = 1 / 4πε₀ = 1) et où la partie angulaire de la métrique s'écrit :

Le potentiel électromagnétique s'écrit dans ce contexte :

.

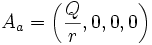Tandis que les trous noirs chargés avec | Q | < M (et surtout avec 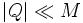) sont similaires aux trous noirs de Schwarzschild, les trous noirs de Reissner-Nordström ont deux horizons : l'horizon des événements et l'horizon interne de Cauchy. Comme pour les autres trous noirs, l'horizon des événements dans l'espace-temps peut être localisé en résolvant l'équation de la métrique : g₀₀ = 0. Les solutions montrent que l'horizon des événements est situé à :

La solution dégénère en une singularité lorsque | Q | = M.

On pense que les trous noirs avec | Q | > M n'existent pas dans la nature, puisqu'ils contiendraient une singularité nue. Leur existence serait en contradiction avec le principe de censure cosmique du physicien britannique Roger Penrose, qui est généralement considéré comme vrai.

Trou noir et supersymétrie

Dans le cadre d'une théorie supersymétrique, comme la théorie des cordes ou même seulement la supergravité, la charge et la masse d'un trou noir sont reliées par l'inégalité de Bogomol'nyi-Prasad-Sommerfield, qui est une conséquence de l'invariance de la théorie sous l'algèbre de superPoincaré. Cette inégalité stipule précisément que

ce qui garantit l'absence de singularités nues dans le cas. Le cas d'égalité correspond à une solution de type trou noir qui préserve la supersymétrie, on parle alors de trou noir critique. La supersymétrie, bien que représentant un élément majeur d'investigation en physique théorique pour une construction d'une physique au-delà du modèle standard n'a cependant pas été observée expérimentalement à ce jour (2006) bien que son existence soit l'un des principaux enjeux des expériences qui seront réalisées dans un futur prochain au LHC. Mais en attendant, la question de l'existence réelle de trous noirs supérsymétriques peut donc être encore considérée comme complètement ouverte.

Généralisation

Si les hypothétiques monopoles magnétiques sont inclus dans la théorie, une généralisation de la métrique ci-dessus s'obtient en incluant une «charge magnétique» P et en remplaçant Q² par Q² + P² et en incluant un terme Pcosθdφ dans l'expression du potentiel électromagnétique.

Références

• Reissner, H, Über due Eigengravitation des elektrischen Felds nach der Einsteinshen Theorie, Ann. Physik, 50, 106-120. (1916).
• Nordström, G, On the Energy of the Gravitational Field in Einstein's Theory, Proc. Kon. Ned. Akad. Wet., 20, 1238-1245. (1918).

Lien externe

• (en) Diagrammes d'espace-temps, par Andrew J. S. Hamilton, incluant un diagramme de Finkelstein et le diagramme de Penrose.

• Portail de l’astronomie