Unités géométriques

En relativité générale, le système d'unités géométriques est un système d'unités réduisant l'ensemble des grandeurs physiques à des longueurs ou des puissances de longueurs. Il vise à proposer une écriture plus simple des équations propres à la relativité générale en omettant deux constantes fondamentales : la vitesse de la lumière c et la constante de gravitation G, c'est-à-dire en considérant que les unités de masse et de temps en vigueur sont telles que ces quantités valent 1. Dans les situations où interviennent des unités électriques, on ajoute la contrainte que la quantité 4πε₀ vaut 1, ε₀ étant la permittivité du vide.

La raison d'être de ce système est de nature mathématique, la relativité générale pouvant être ainsi formalisée sans l'utilisation des contantes fondamentales : la présence et la valeur de celles-ci dépendent uniquement des choix (qui d'un point de vue théorique apparaît quelque peu arbitraire, quoiqu'ils aient bien sûr en pratique des raisons d'être pertinentes) des différentes constantes fondamentales.

Ainsi, les équations d'Einstein s'écrivent-elles dans le système international d'unités

,

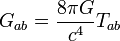où G_ab est le tenseur d'Einstein et T_ab le tenseur énergie-impulsion de la matière. En unités géométriques, il s'écrit plus simplement

G_ab = 8πT_ab.

les composantes du tenseur énergie impulsion étant implicitement modifiées du facteur numérique ad hoc pour la validité de l'égalité.

Sommaire 1 Tableau de conversion 2 Conversion géométrique des SI unités de base 3 Exemple 4 Avantages et inconvénients 5 Référence

Tableau de conversion

Plus généralement, le tableau ci-dessous donne les unités de certaines grandeurs physiques ; leur unité réduite dans le système géométrique ; et le facteur par lequel elles sont multipliées pour passer de leur valeur à leur valeur réduite.

À noter que cette table de conversion dépend explicitement de la dimension de l'espace-temps, considérée égale à quatre ci-après. En effet, la dimension de la constante gravitationnelle dépend explicitement du nombre de dimensions de l'espace.

Grandeur	Dimension SI	Dimension géométrique	Facteur multiplicatif
Longueur	[L]	[L]	1
Durée	[T]	[L]	c-1
Masse	[M]	[L]	G c-2
Vitesse	[L T-1]	1	c-1
Vitesse angulaire	[T-1]	[L-1]	c-1
Accélération	[L T-2]	[L-1]	c-2
Énergie	[M L2 T-2]	[L]	G c-4
Densité d'énergie	[M L-1 T-2]	[L-2]	G c-4
Moment cinétique	[M L2 T-1]	[L2]	G c-3
Force	[M L T-2]	1	G c-4
Puissance	[M L2 T-3]	1	G c-5
Pression	[M L-1 T-2]	[L-2]	G c-4
Masse volumique	[M L-3]	[L-2]	G c-2
Charge électrique	[I T]	[L]	G1/2 c-2 (4πε0)-1/2
Potentiel électrique	[M L2 T-3 I-1]	1	G1/2 c-2 (4πε0)1/2
Champ électrique	[M L T-3 I-1]	[L-1]	G1/2 c-2 (4πε0)1/2
Champ magnétique	[M T-2 I-1]	[L-1]	G1/2 c-1 (4πε0)1/2
Potentiel vecteur	[M L T-2 I-1]	1	G1/2 c-1 (4πε0)1/2

Dans le tableau ci-dessus, les quantités L, T, M et I se réfèrent respectivement à des longueurs, durées, masses et intensités électriques.

Conversion géométrique des SI unités de base

Conversion des kg,s,C,K en m:

• G/c² [m/kg]
• c [m/s]
• ((G/(4*π*ε₀))^0.5)/c² [m/C]
• (G*k)/c⁴ [m/K]

Conversion des m,s,C,K en kg:

• c²/G [kg/m]
• c³/G [kg/s]
• 1/(G*4*π*ε₀)^0.5 [kg/C]
• k/c² [kg/K]

Conversion des m,kg,C,K en s

• 1/c [s/m]
• G/c³ [s/kg]
• ((G/(4*π*ε₀))^0.5)/c³ [s/C]
• (G*k)/c⁵ [s/K]

Conversion des m,kg,s,K en C

• c²/((G/(4*π*ε₀))^0.5) [C/m]
• (G*4*π*ε₀)^0.5 [C/kg]
• c³/((G/(4*π*ε₀))^0.5) [C/s]
• (k*(G*4*π*ε₀)^0.5)/c² [C/K]

Conversion des m,kg,s,C en K

• c⁴/(G*k) [K/m]
• c²/k [K/kg]
• c⁵/(G*k) [K/s]
• c²/(k*(G*4*π*ε₀)^0.5) [K/C]

Exemple

La composante temporelle g_tt de la métrique d'un trou noir de Reissner-Nordström de masse m et de charge électrique q s'écrit

.

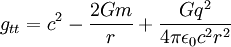Dans le système d'unités géométriques, cette quantité devient

,

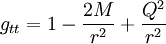où cette fois la composante se transforme en un nombre sans dimension (par division par c²), et la masse M et la charge Q sont écrites en unités géométriques, c'est-à-dire que numériquement elles correspondent à

,

.

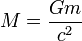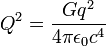Avantages et inconvénients

L'écriture des différentes formules affranchie de leurs unités du système international est significativement plus simple (voir l'exemple ci-dessus). Par contre, elle présente l'inconvénient de rendre souvent plus difficile l'évaluation des ordres de grandeur. En particulier, les calculs du rayonnement gravitationnel d'un système astrophysique sont bien plus facilement interprétables en unités SI qu'en unités géométriques. De plus, dans les situation où la constante de gravitation G est variable au cours du temps (théorie tenseur-scalaire), le système d'unités géométriques ne peut être employé qu'avec circonspection.

Référence

(en) Robert M. Wald, General Relativity, University of Chicago Press, 1984, 498 pages (ISBN 0226870332), page 470 et 471.

• Portail de la physique