- Métrique de Kerr-Newman
-
Trou noir de Kerr-Newman
Pour les articles homonymes, voir Trou noir (homonymie).Article principal : Trou noir.En astronomie, un trou noir de Kerr-Newman est un trou noir de masse M avec une charge électrique Q non-nulle et un moment angulaire J également non nul. Il tient son nom du physicien Roy Kerr, découvreur de la solution de l'équation d'Einstein dans le cas d'un trou noir en rotation non-chargé, et Ezra T. Newman, co-découvreur de la solution pour une charge non-nulle, en 1965.
Le trou noir de Kerr-Newmann est décrit par la métrique du même nom, qui s'écrit :
![ds^{2}=-\frac{\Delta}{\rho^{2}}\left(dt-a\sin^{2}\theta d\phi\right)^{2}+\frac{\sin^{2}\theta}{\rho^{2}}\left[\left(r^{2}+a^{2}\right)d\phi-{a}dt\right]^{2}
+\frac{\rho^{2}}{\Delta}dr^{2}+\rho^{2}d\theta^{2}](/pictures/frwiki/50/234236b37c4f31ef36af209ca5c56c11.png)
où :
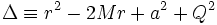
et :
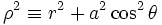
et finalement :
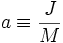
où M est le masse du trou noir, J est le moment angulaire et Q la charge électrique et où les unités géométriques ont été utilisées (c'est-à-dire que les constantes comme la vitesse de la lumière et la constante gravitationnelle sont égales à 1).
Quand Q = a = 0, la métrique de Kerr-Newmann se réduit à la métrique de Schwarzschild (cas non-chargé et sans rotation). Lorsque a = 0, elle se réduit à la métrique de Reissner-Nordström, et lors que Q = 0 à la métrique de Kerr. Lorsque M = Q = 0, le cas se réduit à la métrique d'un espace de Minkowski vide, mais dans des coordonnées sphéroïdales peu habituelles.
De la même manière que la métrique de Kerr, celle de Kerr-Newmann décrit un trou noir seulement lorsque
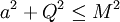.Le résultat de Newmann représente la solution la plus générale de l'équation d'Einstein pour le cas d'un espace-temps stationnaire, axisymétrique, et asymptotiquement plat en présence d'un champ électrique en 4 dimensions. Bien que la métrique de Kerr-Newmann représente une généralisation de la métrique de Kerr, elle n'est pas considérée comme très importante en astrophysique puisque des trous noirs «réalistes» n'auraient généralement pas une charge électrique importante.
Sommaire
Références
- (en) Newman, E. T.; Couch, R.; Chinnapared, K.; Exton, A.; Prakash, A.; and Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 6, 918-919, 1965
Voir aussi
Liens internes
Liens externes
- (en) Kerr-Newman Black Hole, sur le site de scienceworld.
Portail de l’astronomie
Catégorie : Trou noir
Wikimedia Foundation. 2010.
