Métrique de Schwarzschild

Pour consulter un article plus général, voir : Trou noir de Schwarzschild.

Karl Schwarzschild (1873-1916).

Article numérisé original de Karl Schwarzchild en allemand.

En astrophysique, dans le cadre de la Relativité générale, la métrique de Schwarzschild est une solution des équations d'Einstein. Elle décrit la géométrie de l'espace-temps lorsqu'elle est déformée par le champ gravitationnel d'une masse sphérique, statique (sans rotation) et non chargée entourée de vide. Cette masse peut être une étoile, une planète ou un trou noir de Schwarzschild.
Cette solution a été découverte par l'astrophysicien allemand Karl Schwarzschild^[1] en décembre 1915^[2]. C'est la première solution exacte des équations d'Einstein comprenant une masse. La communauté scientifique considère qu'elle est adaptée aux problèmes astrophysiques où le champ gravitationnel et le moment angulaire de la masse centrale sont faibles. Dans le système solaire par exemple, on peut parfaitement considérer la masse totale des planètes comme négligeable par rapport au Soleil. La vitesse de rotation du Soleil est elle-même quasiment nulle si on la compare à la vitesse de la lumière.

Sommaire

1 Conventions mathématiques
2 Diagonalisation de la métrique
3 Simplification des composantes de la métrique
4 Équations de champs
5 Approximation du champ faible
6 L'horizon de Schwarzschild
7 Au-delà de l'horizon: les coordonnées de Kruskal-Szekeres
8 La singularité
9 Notes
10 Lien externe

Conventions mathématiques

On utilise le système de coordonnées $\left(t, r, \theta, \phi\right)$ désignant respectivement le temps, la distance radiale, la colatitude et la longitude. Ces variables peuvent prendre les valeurs suivantes.

$\begin{cases} t\in\mathbb R \\ r\in\mathbb{R}^+ \\ \theta\in\left[0, \pi\right] \\ \phi\in\left[0, 2\pi\right] \end{cases}$

Le cas considéré par Karl Schwarzschild est celui d'un espace symétrique, sphérique, statique, non chargé et vide à l'extérieur du corps central. Mathématiquement, cela signifie que :

Un espace-temps avec symétrie sphérique, on dit aussi isotrope, est un espace-temps où toutes les composantes de la métrique sont inchangées lors d'une opération de rotation. Mathématiquement, les transformations $\theta \rightarrow - \theta$ et $\phi \rightarrow - \phi$ laissent la métrique inchangée.
Un espace-temps est statique lorsque les composantes de la métriques sont indépendants du temps. Mathématiquement, la transformation $t \rightarrow t+a$ n'a pas d'incidence sur la métrique. Cela implique que $\part_t g_{\mu \nu} = 0\,$ , où l'on a utilisé la convention $\part_t \equiv \frac {\part}{\part t}$ .
Une solution dans le vide est une solution pour laquelle le tenseur énergie-impulsion de l'équation d'Einstein est nul : $T_{\mu\nu}=0\,$ en dehors du corps central. Pour le cas d'une constante cosmologique nulle, cela implique que $R_{\mu\nu}=0\,$ , où $R_{\mu\nu}\,$ est le tenseur de Ricci.

On utilise par défaut la signature métrique LLSC^[3] suivante (— + + +).

$+ \mathbf{g} = -(\mathbf{x}^0)^2 + (\mathbf{x}^1)^2 + (\mathbf{x}^2)^2 + (\mathbf{x}^3)^2$

Diagonalisation de la métrique

Les conditions sur l'espace-temps décrites plus haut permettent de simplifier la métrique. Par exemple, la condition d'un espace-temps statique impose que si l'on applique la transformation de coordonnées $(t, r, \theta, \phi) \rightarrow (-t, r, \theta, \phi)$ , les coefficients de la métrique changent de la manière suivante :

$g_{\mu t}'=\frac{\part x^{\alpha}}{\part x^{'\mu}} \frac{\part x^{\beta}}{\part x^{'t}} g_{\alpha \beta}= - g_{\mu t}$ ( $\mu \ne t$ )

Mais, on a imposé que $g' μ t = g μ t$ . Ce qui implique que :

$g_{\mu t}=\, 0$ ( $\mu \ne t$ )

De manière similaire, les transformations de coordonnées $(t, r, \theta, \phi) \rightarrow (t, r, -\theta, \phi)$ et $(t, r, \theta, \phi) \rightarrow (t, r, \theta, -\phi)$ donnent respectivement :

$g_{\mu \theta}=\, 0$ ( $\mu \ne \theta$ )

$g_{\mu \phi}=\, 0$ ( $\mu \ne \phi$ )

En combinant tous ces résultats, on obtient :

$g_{\mu \nu }=\, 0$ ( $\mu \ne \nu$ )

En conséquence, la métrique a la forme suivante :

$ds^2=\, g_{tt} dt ^2 + g_{rr}d r^2 + g_{\theta\theta} d \theta ^2 + g_{\phi\phi} d \phi ^2$

où les quatre composantes de la métrique ( $g t t$ , $g r r$ , $g θθ$ et $g ϕϕ$ ) sont indépendantes de la coordonnée de temps.

Simplification des composantes de la métrique

Sur chaque hypersurface où $t$ , $θ$ et $ϕ$ sont constants (i.e. sur chaque ligne radiale), $g r r$ ne doit dépendre que de $r$ (par la condition de symétrie sphérique). Donc $g r r$ est une fonction d'une seule variable :

$g_{rr}=A\left(r\right)$

Un argument similaire appliqué à $g t t$ implique que :

$g_{tt}=B\left(r\right)$

Sur les hypersurfaces où $t$ et $r$ sont constants, on impose que la métrique est celle d'une 2-sphère :

$dl^2=r_{0}^2 (d \theta^2 + \sin^2 \theta d \phi^2)$

En choisissant une de ces hypersurfaces (celle avec un rayon $r 0$ ), les composantes de la métrique restreintes à cette surface (que l'on dénotera $\tilde{g}_{\theta\theta}$ et $\tilde{g}_{\phi\phi}$ ) doivent être inchangées sous les opérations de rotation de $θ$ et $ϕ$ (de nouveau, par symétrie sphérique). Ainsi, comparant les formes de la métrique de cette hypersurface donne :

$\tilde{g}_{\theta\theta}\left(d \theta^2 + \frac{\tilde{g}_{\phi\phi}}{\tilde{g}_{\theta\theta}} d \phi^2 \right) = r_{0}^2 (d \theta^2 + \sin^2 \theta d \phi^2)$

ce qui implique immédiatement :

$\tilde{g}_{\theta\theta}=r_{0}^2$ et $\tilde{g}_{\phi\phi}=r_{0}^2 \sin ^2 \theta$

Comme cela est imposé pour chaque hypersurface (en d'autres termes pour une quelconque valeur de $r$ ), on a :

$g_{\theta\theta}=\, r^2$ et $g_{\phi\phi}=\, r^2 \sin^2 \theta$

Ainsi, la métrique peut être écrite sous la forme :

$ds^2= B\left(r\right) dt^2 + A\left(r\right)dr^2+r^2d \theta^2+r^2 \sin^2 \theta d \phi^2$

où $A$ et $B$ sont des fonctions de $r$ encore à déterminer. $A$ et $B$ doivent être non-nulles partout (ou alors la métrique serait singulière en ces points).

Équations de champs

Afin de déterminer les fonctions $A$ et $B$ , on utilise l'équation d'Einstein dans le vide mentionnée plus haut :

$R_{\mu\nu}=\, 0$

où $R μν$ est le tenseur de Ricci. Parmi ces équations, seules quatre sont non-triviales, et après simplification, on obtient :

$4 \part_r(A) B^2 - 2 r \part_r^2(B) AB + r \part_r(A) \part_r(B)B + r \part_r(B) ^2 A=0$

$r \part_r(A)B + 2 A^2 B - 2AB - r \part_r(B) A=0\,$

$- 2 r \part_r^2(B) AB + r \part_r(A) \part_r(B)B + r \part_r(B) ^2 A - 4\part_r(B) AB=0$

La quatrième équation est simplement la deuxième multipliée par $sin 2 θ$ . En soustrayant la première et la troisième, on obtient :

$\part_r(A)B +A \part_r(B)=0 \rightarrow A(r)B(r) =K\,$

où $K$ est une constante non-nulle. En remplaçant $A(r)B(r) \, =K$ dans la deuxième équation, et en simplifiant, on a :

$r \part_r(A) =A(1-A)\,$

dont la solution générale est :

$A(r)=\left(1+\frac{1}{Sr}\right)^{-1}\,$

avec une constante réelle non-nulle $S$ . En conséquence, la métrique pour une solution statique, symétriquement sphérique et dans le vide, s'écrit :

$ds^2=K \left(1+\frac{1}{S r}\right)dt^2 + \left(1+\frac{1}{S r}\right)^{-1}dr^2+r^2(d \theta^2 + \sin^2 \theta d \phi^2)\,$

L'espace-temps représenté par cette métrique est asymptotiquement plat. Lorsque $r \rightarrow \infty$ , la métrique s'approche de celle de Minkowski, et la variété de l'espace-temps ressemble à celle de l'espace de Minkowski.

Approximation du champ faible

Représentation de la déformation de l'espace-temps en présence d'une masse centrale. Plus la déformation est forte et plus on s'éloigne du plan euclidien.

Pour calculer les constantes $K$ et $S$ , on utilise l'« approximation du champ faible ». C'est-à-dire que l'on se place loin du centre, là où le champ de gravitation est faible. On considère donc une condition aux limites. À l'infini, la métrique de Schwarzschild doit être identique à l'espace plat de Minkowski. En partant des résultats généraux de la relativité restreinte, toutes les composantes de la métrique peuvent être déterminées sans faire appel au calcul tensoriel^[4].
$G$ est la constante gravitationnelle, $M$ est la masse de l'objet central, et $c$ est la vitesse de la lumière.

Estimation de la première fonction $g t t$ .

On considère un événement fixe : $d r = d θ = d ϕ = 0$ . Le temps propre est alors donné par :

$ds^2\equiv d\tau^2$

d τ 2 = g t t c 2 d t 2

Le principe d'équivalence nous donne l'expression entre la coordonnée temporelle et le temps propre mesuré dans l'entourage de la distribution de masse.

$d\tau\simeq \frac{dt}{(1+\frac{GM}{c^2r})}=\frac{dt}{(1+\frac{\Delta U}{c^2})}$

$d\tau^2\simeq (1+\frac{GM}{c^2r})c^2dt^2$

On considère maintenant une expérience de chute libre. Une particule tombe lorsqu'elle est soumise au champ de gravitation. Elle possède les vitesses $v A$ et $v B$ lorsqu'elle se situe aux points A et B. On applique la loi de conservation de l'énergie.

$\frac{E}{M}=\frac{1}{2}v_A^2 + U_A=\frac{1}{2}v_B^2 + U_B$

$\frac{1}{2}(\frac{v_A^2}{c^2} - \frac{v_B^2}{c^2})=\frac{U_B-U_A}{c^2}=-\frac{\Delta U}{c^2}$

En relativité restreinte, si $τ$ représente le temps propre de notre particule, on a :

$\frac{t_B}{t_A}=\frac{\tau \sqrt{1-\frac{v_B^2}{c^2}}}{\tau \sqrt{1-\frac{v_A^2}{c^2}}} \simeq 1 + \frac{1}{2}\left(\frac{v_A^2}{c^2}-\frac{v_B^2}{c^2}\right) =- \frac{\Delta U}{c^2}$

Avec les estimations précédentes, dans le cas où le champ est faible, on a : $g_{tt} \simeq \left(1-\frac{2GM}{c^2 r} \right)$

Estimation des fonctions $g r r$ .

Faisons l'hypothèse que le déterminant du tenseur métrique est approximativement minkowskien.

Dans ce cas, il est diagonal et nous avons : $\begin{cases} g = -1 & \text{en coordonnees cartesiennes}\\ g=-r^4sin^2\theta & \text{en coordonnees spheriques}\end{cases}$

Puisque la métrique est lorentzienne à l'infini, nous avons : $g t t g r r = - 1$ . L'approximation de $g t t$ fournit celle de $g r r$ $g_{rr}=- (g_{tt})^{-1} \simeq - \left(1-\frac{2GM}{c^2 r} \right)^{-1}$

En utilisant par convention la signature (— + + +) les deux premières composantes du tenseur métrique sont :

$g_{rr} =- (g_{tt})^{-1} \simeq \left(1-\frac{2GM}{c^2 r} \right)^{-1}$

Estimation des fonctions $g θθ$ et $g φφ$ .

Puisqu'en coordonnées sphériques : $g = g t t g r r g θθ g ϕϕ = - r 4 s i n 2 θ$ , avec la même convention pour la signature métrique et les résultats obtenus pour les premières composantes, on déduit la relation : $g θθ g ϕϕ = r 4 s i n 2 θ$

$g θθ = r 2$ et $g ϕϕ = r 2 s i n 2 θ$

La métrique de Schwarzschild peut finalement s'écrire sous la forme suivante :

$ds^2= - \left(1-\frac{2GM}{c^2 r}\right)c^2dt^2 + \left(1-\frac{2GM}{c^2 r}\right)^{-1}dr^2+r^2(d \theta^2 +\sin^2 \theta d \phi^2)$ .

En utilisant la convention $G = c = 1$ :

$ds^2=- \left(1-\frac{2M}{r}\right)dt^2 + \left(1-\frac{2M}{r}\right)^{-1}dr^2+r^2(d \theta^2 +\sin^2 \theta d \phi^2)$ .

Une singularité est atteinte lorsque $\left(1-\frac{2M}{r}\right) = 0$ , c'est-à-dire lorsque la coordonnée du rayon $r$ vaut : $2 M$ .

Ce rayon est appelé le rayon de Schwarzschild, le rayon gravitationnel, la surface de Schwarzschild, l'horizon de Schwarzschild, la sphère de Schwarzschild ou encore la singularité de Schwarzschild. Cette dernière expression, maintenant désuète, est surtout utilisée dans l'ancienne littérature scientifique.

L'horizon de Schwarzschild

Animation de la géométrie de l'espace-temps de Schwarzschild. La courbure croit avec la masse. Elle devient infinie uniquement au centre.

Lorsque $r = 2 M$ , le coefficient $g t t$ de la métrique tend vers zéro et $g r r$ devient infini. On nomme ce rayon l'horizon des événements. Lorsque $r = 2 M$ on peut voir que le rôle de $r$ et $t$ comme coordonnée spatiale et temporelle est inversé. Dans la région $r > 2 M$ , la direction de $t$ est du type temps ( $g t t < 0$ ) et celle de $r$ de type espace ( $g r r > 0$ ). La direction s'inverse lorsque un observateur franchit l'horizon des événements. Cela signifie qu'à l'intérieur du rayon de Schwarzschild, la distance d'un observateur à $r = 0$ est une mesure temporelle !

Cette singularité de la métrique est apparente car il s'agit d'une pathologie du système de coordonnées utilisé. Si nous étions en présence d'une véritable singularité, c'est-à-dire une région de l'espace-temps où les quantités physiques telles que l'énergie, la pression… deviennent infinies, alors la courbure de la métrique exprimée par le tenseur de Riemann serait elle-même infinie. Or cette courbure est parfaitement déterminée lorsqu'un observateur franchit le rayon de Schwarzschild. L'invariant de courbure $K = M / r 3$ est régulier. Les composantes du tenseur de courbure de Riemann sont infinies uniquement lorsque $r = 0$ .

Il est possible d'établir un jeu de coordonnées, plus adaptées pour un observateur comobile s'approchant du corps céleste, dans lequel la métrique est parfaitement régulière au niveau de l'horizon. Un observateur traversant l'horizon ne détecterait donc pas d'évènement particulier. Un exemple est fourni par les coordonnées de Kruskal-Szekeres. Dans le cas idéalisé où le corps céleste est ponctuel au centre de la région interne à l'horizon, on peut montrer qu'il y existe une singularité réelle. À cet endroit un observateur détecterait nécessairement une divergence de toutes les quantités physiques observables.

Puisque l'horizon des événements dépend uniquement de la masse $M$ , on peut déterminer les rayons de Schwarzschild des différents corps célestes usuels.

Paramètres physiques et rayon de Schwarzschild approximatif de quelques corps célestes.
Objet céleste	Masse	Rayon	Rayon de Schwarzschild
Terre	$6.10 24$ kg	$6.10 3$ km	0,9 cm
Jupiter	$2.10 27$ kg	$7.10 4$ km	3 m
Soleil	$2.10 30$ kg	$7.10 5$ km	3 km
Pulsar	$2.10 30$ kg	10 km	3 km
Sirius A	2 $M_{\odot}$	1,75 $R_{\odot}$	6 km

Au-delà de l'horizon: les coordonnées de Kruskal-Szekeres

Éléments historiques

Arthur Stanley Eddington (1882-1944).

Les équations d'Einstein étant covariantes, les physiciens et mathématiciens ont cherchés de nouveaux systèmes de coordonnées sans singularité et surtout plus susceptibles de représenter la totalité de la géométrie de Schwarzschild. Paul Painlevé et Allvar Gullstrand ou encore Georges Lemaître ont publié plusieurs tentatives dans ce domaine. Mais c'est au physicien Arthur Eddington que l'on crédite la création du premier système de coordonnées non singulier à $r = 2 M$ en 1924^[5]. Pourtant, Synge démontrera que le système d'Eddington-Finkelstein - il est redécouvert par Finkelstein dans les années 50 - ne recouvre qu'une partie de la géométrie de l'espace-temps de Schwarzschild^[6]. Il faudra attendre les années 60, pour qu'indépendamment l'un de l'autre, Martin Kruskal et George Szekeres réussissent à établir des coordonnées où les géodésiques peuvent traverser la singularité apparente.
Ce système est très souvent étudié car la variété de Kruskal-Szekeres est l'extension analytique maximale de la variété de Schwarzschild^[7].

Les coordonnées de Kruskal-Szekeres

Conventions mathématiques: on utilise les unités naturelles ( $G = c = 1$ ). La signature de la métrique est (– + + +).

Kruskal et Szekeres utilisent des coordonnées sans dimension. $u$ pour la coordonnée radiale. $v$ pour la coordonnée temporelle.
Elles sont définies par des fonctions transcendantes - dont le but est d'éliminer le terme $(1 - 2 M / r)$ - par la relation :

$u 2 - v 2 = (r / 2 M - 1) e r / 2 M$

De plus, elles différencient deux régions différentes de la géométrie de Schwarzschild :

Si $r > 2 M$ alors $\begin{cases} u = (r/2M -1)^{1/2}e^{r/4M}cosh(t/4M) \\ v = (r/2M -1)^{1/2}e^{r/4M}sinh(t/4M) \end{cases}$

Si $r < 2 M$ alors $\begin{cases} u = (1-r/2M)^{1/2}e^{r/4M}sinh(t/4M) \\ v = (1-r/2M)^{1/2}e^{r/4M}cosh(t/4M) \end{cases}$

On obtient la métrique diagonale :

$ds^2 = \frac{32M^3}{r}e^{-r/2M}(du^2 - dv^2) + r^2(d\theta^2 + sin^2\theta d \phi^2)$

Propriétés

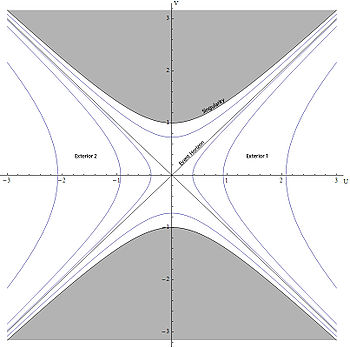
Representation en coordonnées de Kruskal-Szekeres.

À la pathologie singulière de la métrique de Schwarzschild à $r = 2 M$ est substituée la relation $v 2 - u 2 = 1$ .

On a donc maintenant deux singularités : $\begin{cases} u = \sqrt{v^2-1} \\ u = - \sqrt{v^2-1} \end{cases}$

Les droites $r = C s t e$ en coordonnées de Schwarzschild sont les hyperboles $u 2 - v 2 = C s t e$ en coordonnées de Kruskal. Leurs asymptotes sont les bissectrices $u = v$ et $u = - v$ . Les droites $t = C s t e$ en coordonnées de Schwarzschild sont les droites $v / u = C s t e$ passant par l'origine en coordonnées de Kruskal. Les singularités sont représentées par les frontières des zones hyperboliques grises sur le dessin ci-contre.

Les géodésiques de type lumière sont les lignes orientées à 45°. Il est facile de vérifier que pour $d s = 0$ , on a $d u 2 = d v 2$ .

La métrique de Schwarzschild différencie deux régions de l'espace-temps délimitées par l'horizon des événements. La région $r > 2 M$ est segmentée en deux avec la métrique de Kruskal-Szekeres.

La condition

r > 2 M

correspond

u 2 > v 2

à $\begin{cases} u > |v| \\ u < - |v| \end{cases}$

La totalité de la géométrie de Schwarzschild est donc représentée par quatre régions différentes en coordonnées de Kruskal.

La singularité

Notes

↑ Schwarzschild, K., Über das Gravitationsfeld eines Massepunktes nach der Einsteinschen Theorie, Preussische Akademie der Wissenschaften, Sitzungberichte, 1916, pp. 189-196.
↑ Johannes Droste, un élève de Hendrik Lorentz, a obtenu indépendamment mais surtout avant Schwarzschild la même solution. Cf. Einstein, A., Œuvres choisies, Relativités I, Ed. Le Seuil, CNRS, Coll. Sources du savoir, n. 9, p. 170. et Einstein, A., Œuvres choisies, Relativités II, n. 18, p. 47.
↑ "Landau-Lifshitz Spacelike Convention" : Convention de type espace de Landau-Lifshitz.
↑ Cette approximation n'est pas la méthode utilisée par Karl Schwarzschild pour établir la métrique qui porte désormais son nom. Celui-ci a utilisé le calcul tensoriel.
↑ Eddington, A. S., A comparaison of Whitehead's and Einstein's formulas, 1924, Nature 113, 192.
↑ Synge, J. L., The gravitational field of a particule, 1950, Proc. R. Irish Acad. A 53, 83-114.
↑ Mavridès, S., L'Univers relativiste, Masson, 1973, p. 338.

LANDAU & LIFCHITZ, théorie du champ, édition de la Paix, Moscou, chapitre X à XII, date impression non mentionnée, environ 1970, remarquable

Lien externe

(en) Schwarzschild Black Hole sur le site scienceworld.wolfram.com

Portail de la physique

Catégorie :

Trou noir

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Métrique de Schwarzschild de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Metrique de Schwarzschild — Métrique de Schwarzschild Pour consulter un article plus général, voir : Trou noir de Schwarzschild. En astrophysique, et plus précisément dans le cadre de la Relativité générale, la métrique de Schwarzschild est une métrique permettant de… … Wikipédia en Français
Métrique De Schwarzschild — Pour consulter un article plus général, voir : Trou noir de Schwarzschild. En astrophysique, et plus précisément dans le cadre de la Relativité générale, la métrique de Schwarzschild est une métrique permettant de décrire le champ… … Wikipédia en Français
Métrique de schwarzschild — Pour consulter un article plus général, voir : Trou noir de Schwarzschild. En astrophysique, et plus précisément dans le cadre de la Relativité générale, la métrique de Schwarzschild est une métrique permettant de décrire le champ… … Wikipédia en Français
Metrique de Kruskal-Szekeres — Métrique de Kruskal Szekeres La métrique de Kruskal Szeres est le prolongement analytique maximal de la métrique de Schwarzschild. L introduction de la métrique de Kruskal Szekeres apporte des solutions supplémentaires à celles de Schwarzschild,… … Wikipédia en Français
Métrique De Kruskal-Szekeres — La métrique de Kruskal Szeres est le prolongement analytique maximal de la métrique de Schwarzschild. L introduction de la métrique de Kruskal Szekeres apporte des solutions supplémentaires à celles de Schwarzschild, on y retrouve notamment un… … Wikipédia en Français
Métrique de kruskal-szekeres — La métrique de Kruskal Szeres est le prolongement analytique maximal de la métrique de Schwarzschild. L introduction de la métrique de Kruskal Szekeres apporte des solutions supplémentaires à celles de Schwarzschild, on y retrouve notamment un… … Wikipédia en Français
Métrique (physique) — Métrique de Schwarzschild Métrique de Friedmann Lemaître Robertson Walker Portail de la physique … Wikipédia en Français
Métrique de Kerr — Trou noir de Kerr Pour les articles homonymes, voir Trou noir (homonymie). Article principal : trou noir. En astrophysique, un trou noir de Kerr désigne un trou noir en rotation et de charge électrique nulle. Il est décrit dans le cadre de… … Wikipédia en Français
Métrique de Kruskal-Szekeres — La métrique de Kruskal Szeres est le prolongement analytique maximal de la métrique de Schwarzschild. L introduction de la métrique de Kruskal Szekeres apporte des solutions supplémentaires à celles de Schwarzschild, on y retrouve notamment un… … Wikipédia en Français
Schwarzschild — Karl Schwarzschild Karl Schwarzschild Karl Schwarzschild (9 octobre 1873, Francfort sur le Main – 11 mai 1916, Potsdam) était un astrophysicien allemand. Sa curiosité pour les étoiles se manifesta dès ses premières an … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'