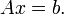Méthode Du Gradient Biconjugué

Méthode du gradient biconjugué

En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d'équations linéaires

$A x= b.\,$

Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite pas que la matrice $A$ soit auto-adjointe, en revanche, la méthode requiert des multiplications par la matrice adjointe $A *$ .

L'algorithme

Choisir $x 0$ , $y 0$ , un préconditionneur régulier $M$ (on utilise fréquemment $M - 1 = 1$ ) et $c$ ;
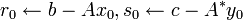$r_0 \leftarrow b-A x_0, s_0 \leftarrow c-A^* y_0\,$ ;
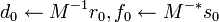$d_0 \leftarrow M^{-1} r_0, f_0 \leftarrow M^{-*} s_0\,$ ;
for 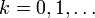$k=0, 1, \dots\,$ do
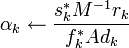$\alpha_k \leftarrow {s^*_k M^{-1} r_k \over f_k^* A d_k}\,$ ;
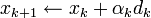
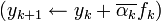$x_{k+1} \leftarrow x_k+ \alpha_k d_k\,$ $\left( y_{k+1} \leftarrow y_k + \overline{\alpha_k} f_k \right)\,$ ;
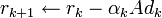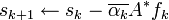$r_{k+1} \leftarrow r_k- \alpha_k A d_k \,$ , $s_{k+1} \leftarrow s_k- \overline{\alpha_k} A^* f_k \,$ ( $r k = b - A x k$ and $s k = c - A * y k$ are the residuums);
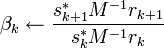$\beta_k \leftarrow {s_{k+1}^* M^{-1} r_{k+1} \over s^*_k M^{-1} r_k}\,$ ;
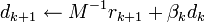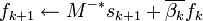$d_{k+1} \leftarrow M^{-1} r_{k+1} + \beta_k d_k\,$ , $f_{k+1} \leftarrow M^{-*} s_{k+1} + \overline{\beta_k} f_k\,$ .

Discussion

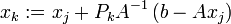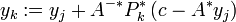La méthode est numériquement instable, mais très importante du point de vue théorique: on définit les itération par $x_k:=x_j+ P_k A^{-1}\left(b - A x_j \right)$ et $y_k:=y_j+A^{-*}P_k^*\left(c-A^* y_j \right)$ ( $j < k$ ) en utilisant les projections suivantes:

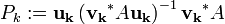$P_k:= \mathbf{u_k} \left(\mathbf{v_k}^* A \mathbf{u_k} \right)^{-1} \mathbf{v_k}^* A$ ,

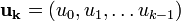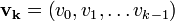Avec $\mathbf{u_k}=\left(u_0, u_1, \dots u_{k-1} \right)$ et $\mathbf{v_k}=\left(v_0, v_1, \dots v_{k-1} \right)$ . On peut irérer les projections elles-mêmes, comme

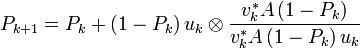$P_{k+1}= P_k+ \left( 1-P_k\right) u_k \otimes {v_k^* A\left(1-P_k \right) \over v_k^* A\left(1-P_k \right) u_k}$ .

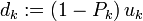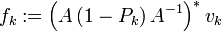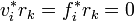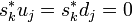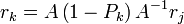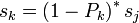Les nouvelles directions de descente $d_k:= \left(1-P_k \right) u_k$ et $f_k:= \left( A \left(1- P_k \right) A^{-1} \right)^* v_k$ sont alors orthogonales aux résidus: $v_i^* r_k= f_i^* r_k=0$ et $s_k^* u_j = s_k^* d_j= 0$ , qui satisfont aux-même $r_k= A \left( 1- P_k \right) A^{-1} r_j$ et $s_k= \left( 1- P_k \right) ^* s_j$ ( $i, j < k$ ).

La méthode du gradient biconjugué propose alors le choix suivant:

u k : = M - 1 r k

v k : = M - * s k

Ce choix particulier permet alors d'éviter une évaluation directe de $P k$ et $A - 1$ , et donc augmented la vitesse d'execution de l'algorithme.

Propriétés

Si $A = A *$ est auto-adjointe, $y 0 = x 0$ et $c = b$ , donc $r k = s k$ , $d k = f k$ , et la méthode du gradient conjugué produit la même suite $x k = y k$ .

En dimensions finies $x n = A - 1 b$ , au plus tard quand $P n = 1$ : La méthode du gradient biconjugué rend la solution exacte après avoir parcouru tout l'espace et est donc une méthode directe.

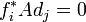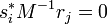La suite produite par l'algorithme est biorthogonale: $f_i^* A d_j = 0$ et $s_i^* M^{-1} r_j=0$ pour $i \ne j$ .

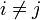SI $p j'$ est un polynôme avec 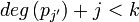$deg\left( p_{j'} \right) +j <k$ , alors 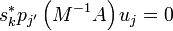$s_k^* p_{j'}\left(M^{-1} A \right) u_j=0$ . L'algorithme est donc composé de projections sur des espaces de Krylov;

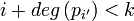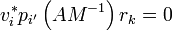SI $p i'$ est un polynôme avec $i+deg\left( p_{i'} \right) <k$ , alors $v_i^* p_{i'}\left(A M^{-1} \right) r_k=0$ .

Portail des mathématiques

Ce document provient de « M%C3%A9thode du gradient biconjugu%C3%A9 ».

Catégories : Optimisation | Analyse numérique matricielle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode Du Gradient Biconjugué de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Methode du gradient biconjugue — Méthode du gradient biconjugué En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué … Wikipédia en Français
Méthode du gradient biconjugué — En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite… … Wikipédia en Français
Methode du gradient conjugue — Méthode du gradient conjugué En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative. La… … Wikipédia en Français
Méthode Du Gradient Conjugué — En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative. La méthode du gradient… … Wikipédia en Français
Méthode du gradient conjugué — En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est définie positive (et par conséquent symétrique). Cette méthode, imaginée en 1950 simultanément par… … Wikipédia en Français
Gradient conjugué — Méthode du gradient conjugué En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative. La… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Stabilité numérique — En analyse numérique, une branche des mathématiques, la stabilité numérique est une propriété globale d’un algorithmique numérique, une qualité nécessaire pour espérer obtenir des résultats ayant du sens. Une définition rigoureuse de la stabilité … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Méthode Du Gradient Biconjugué