Methode du gradient conjugue
- Methode du gradient conjugue
-
Méthode du gradient conjugué
En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d'équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative.
La méthode du gradient biconjugué fournit une généralisation pour les matrices non symétriques.
Principe
L'objectif est de minimiser la fonction 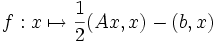 où A est une matrice carrée symétrique définie positive de taille n.
où A est une matrice carrée symétrique définie positive de taille n.
Le calcul montre qu'une solution du problème est la solution du système Ax = b : en effet , on a 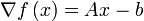 .
.
La méthode du gradient conjugué consiste donc à construire par récurrence une base de vecteurs de  orthogonaux pour le produit scalaire
orthogonaux pour le produit scalaire 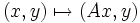 , et exprimer le vecteur solution dans cette base.
, et exprimer le vecteur solution dans cette base.
Implémentation
Un exemple d'implémentation pour Octave:
function [x] = conjgrad(A,b,x0)
r = b - A*x0;
w = -r;
z = A*w;
a = (r'*w)/(w'*z);
x = x0 + a*w;
B = 0;
for i = 1:size(A)(1);
r = r - a*z;
if( r < 1e-10 )
break;
endif
B = (r'*z)/(w'*z);
w = -r + B*w;
z = A*w;
a = (r'*w)/(w'*z);
x = x + a*w;
end
Liens
 Portail des mathématiques
Portail des mathématiques
Catégorie : Analyse numérique matricielle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Methode du gradient conjugue de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Méthode Du Gradient Conjugué — En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative. La méthode du gradient… … Wikipédia en Français
Méthode du gradient conjugué — En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est définie positive (et par conséquent symétrique). Cette méthode, imaginée en 1950 simultanément par… … Wikipédia en Français
Gradient conjugué — Méthode du gradient conjugué En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative. La… … Wikipédia en Français
Methode du gradient biconjugue — Méthode du gradient biconjugué En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué … Wikipédia en Français
Méthode Du Gradient Biconjugué — En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite… … Wikipédia en Français
Méthode du gradient biconjugué — En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite… … Wikipédia en Français
Méthode de résolution numérique — Analyse numérique Simulation numérique d un crash de véhicule L’analyse numérique est une discipline des mathématiques. Elle s’intéresse tant aux fondements théoriques qu’à la mise en pratique des méthodes permettant de résoudre, par des calculs… … Wikipédia en Français
Méthode numérique — Analyse numérique Simulation numérique d un crash de véhicule L’analyse numérique est une discipline des mathématiques. Elle s’intéresse tant aux fondements théoriques qu’à la mise en pratique des méthodes permettant de résoudre, par des calculs… … Wikipédia en Français
Algorithme du gradient — L algorithme du gradient désigne un algorithme d optimisation différentiable. Il est par conséquent destiné à minimiser une fonction réelle différentiable définie sur un espace euclidien (par exemple, , l espace des n uplets de nombres réels,… … Wikipédia en Français
Descente De Gradient — Traduction à relire Gradient descent → … Wikipédia en Français
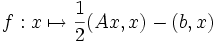 où A est une matrice carrée symétrique définie positive de taille n.
où A est une matrice carrée symétrique définie positive de taille n.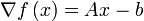 .
. orthogonaux pour le produit scalaire
orthogonaux pour le produit scalaire 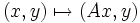 , et exprimer le vecteur solution dans cette base.
, et exprimer le vecteur solution dans cette base.