Preconditionneur

Preconditionneur

Préconditionneur

En algèbre linéaire et en analyse numérique, un préconditionneur P d'une matrice A est une matrice telle que le conditionnement de P − 1A est plus petit que celui de A.

Le préconditionnement est surtout utilisé dans les méthodes itératives pour la résolution d'un système linéaire (méthode du gradient, méthode du gradient conjugué, ...).

Au lieu de résoudre,

Ax=b\,

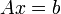
on préfère résoudre

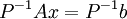
P^{-1}Ax=P^{-1}b\,

qui permet de diminuer considérablement le nombre d'itérations dans la méthode de résolution (itérative). On dit que le système est "mieux" conditionné.


Ici, nous avons écrit un préconditionneur à gauche. Nous pouvons aussi écrire un préconditionneur à droite. Dans ce cas, la résolution se fait en deux temps: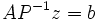

AP^{-1} z=b\, et x = P − 1z


Nous pouvons, dans la même idée, écrire un préconditionneur à droite et à gauche, c'est-à-dire: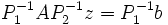

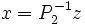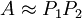
P^{-1}_1AP^{-1}_2z=P^{-1}_1b\, avec x=P^{-1}_2z et A \approx P_1P_2


En général, on ne calcule pas explicitement P, mais on utilise des algorithmes pour trouver un inverse approché de A ( SPAI, décomposition LU, factorisation de Cholesky, ...). Dans certaines méthodes numériques (intégrales de frontières avec décomposition multipôles, ...), on préfère définir le produit matrice-vecteur, ce qui permet de réduire le stockage de(s) matrice(s), donc certains types de préconditionneur seront préférés.

Sources

  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « preconditioner ».
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Pr%C3%A9conditionneur ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Preconditionneur de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Préconditionneur — En algèbre linéaire et en analyse numérique, un préconditionneur P d une matrice A est une matrice telle que le conditionnement de P − 1A est plus petit que celui de A. Le préconditionnement est surtout utilisé dans les méthodes itératives pour… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Methode du gradient biconjugue — Méthode du gradient biconjugué En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué …   Wikipédia en Français

  • Méthode Du Gradient Biconjugué — En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite… …   Wikipédia en Français

  • Méthode du gradient biconjugué — En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite… …   Wikipédia en Français

  • Méthode du gradient conjugué — En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est définie positive (et par conséquent symétrique). Cette méthode, imaginée en 1950 simultanément par… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”