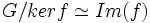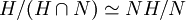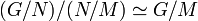- Morphisme de groupe
-
Morphisme de groupes
Un morphisme de groupes ou homomorphisme de groupes est une application entre deux groupes qui respecte la structure des groupes.
Plus précisément, si (G,*) et (G',
) sont deux groupes de neutres respectifs e et e', une application 
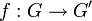est un morphisme du groupes lorsque :Les deux propriétés suivantes sont des conséquences immédiates de la définition :
On dit que f est un isomorphisme de groupes si f est un morphisme bijectif. Dans ce cas, f-1 est aussi un morphisme de groupes. Si de plus,
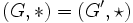, on parle d'automorphisme du groupe G .Un morphisme de groupe transporte la loi de groupe, et va ainsi conserver toutes les propriétés liées à cette loi. Il est donc intéressant d'étudier comment se comportent les principaux objets de la théorie des groupes par les morphismes.
Sommaire
Liens avec les sous-groupes
Soient
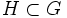un sous-groupe de 
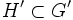un sous-groupe de 
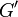.On a alors:
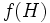est un sous-groupe de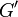 
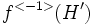est un sous-groupe de
Par ailleurs:Si
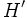est un sous-groupe distingué de 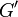, alors 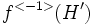est un sous-groupe distingué de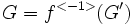 
note: dans le cas où
est surjectif, on a 
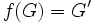et donc 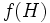est un sous-groupe distingué de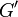 Noyau et image
Par définition, on appelle noyau (Kern en allemand, kernel en anglais) du morphisme f, l'ensemble :
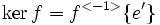
L'image de f est définie par :
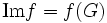
On a les propriétés suivantes :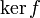
est un sous-groupe distingué de .
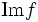est un sous-groupe de .
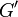Équivalence fondamentale :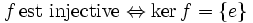
Isomorphismes de groupe
On suppose dans cette section que f est un isomorphisme. Cela revient à dire que c'est un morphisme bijectif.
On dit alors que les deux groupes G et G' sont isomorphes.
L'application réciproque f − 1 de G' vers G est également un isomorphisme de groupe.
Les deux groupes G et G' vont avoir exactement les mêmes propriétés, c'est-à-dire que du point de vue de la théorie des groupes ils se comportent comme étant le même objet.
Théorèmes d'isomorphismes
Article détaillé : Théorèmes d'isomorphisme.f induit un isomorphisme du groupe quotient
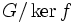vers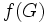 
On peut noter mathématiquement cet isomophisme par :
On déduit de ce théorème fondamental deux autres théorèmes d'isomorphisme.
Deuxième théorème d'isomorphisme
Si N est un sous-groupe normal de G et H un sous-groupe de G, alors
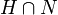est un sous-groupe normal de H et on a l'isomorphisme suivant :Troisième théorème d'isomorphisme
Soit N et M deux sous-groupes normaux de G tels que M est inclus dans N. N/M est alors un sous-groupe normal de G/M et on a l'isomorphisme suivant :
Ces trois théorèmes d'isomorphisme sont généralisables à d'autres structures que les groupes. Voir notamment Algèbre universelle#Passage au quotient et théorèmes d'isomorphie.
Bibliographie
- Elements de théorie des groupes , Josette Calais , PUF , Paris 1984.
- Algèbre générale , Bernard Charles et Denis Allouch , PUF , Paris , 1984.
Portail des mathématiques
Catégorie : Théorie des groupes
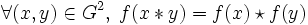
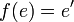
![\forall x \in G,\; f(x^{-1})=[f(x)]^{-1} \,](/pictures/frwiki/51/306e1dab4d1ce0c7f06ddaf855684ab1.png)
Wikimedia Foundation. 2010.
