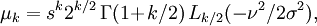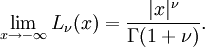- Loi de rice
-
Loi de Rice
En statistiques et théorie des probabilités, la loi de Rice est une loi statistique continue (c'est-à-dire à densité). C'est la loi que suit la racine carrée d'une χ².
Rice Densité de probabilité / Fonction de masse
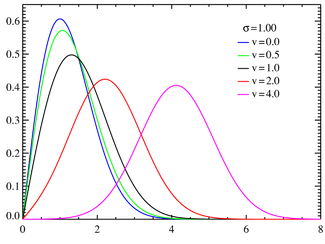
Densité de probabilité de la loi de Rice pour différentes valeurs de ν avec σ = 1.
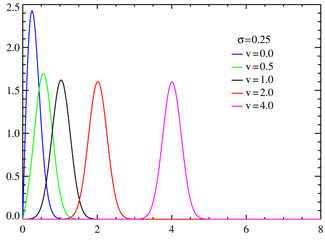
Densité de probabilité de la loi de Rice pour différentes valeurs de ν avec σ = 0,25.Fonction de répartition
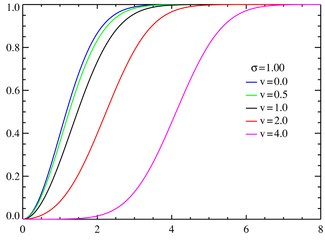
Fonction de répartition pour la loi de Rice avec σ = 1,0 pour différentes valeurs de ν.
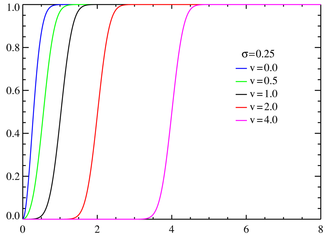
Fonction de répartition pour la loi de Rice avec σ = 0,25 pour différentes valeurs de ν.Paramètres 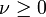
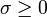
Support 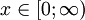
Densité de probabilité (fonction de masse) 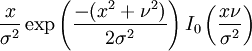
Fonction de répartition 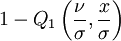
où Q1 is the Marcum Q-Function
Espérance 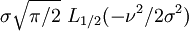
Médiane (centre) Mode Variance 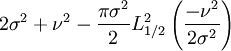
Asymétrie (statistique) (compliqué) Kurtosis (non-normalisé) (compliqué) Entropie Fonction génératrice des moments Fonction caractéristique Sommaire
Caractérisation
Sa densité de probabilité vaut
avec
Γ étant la fonction gamma d'Euler.
Lorsque q prend la valeur 2, on retrouve une Loi de Rayleigh.
Une autre formulation consiste à considérer:
où I0(z) est la Fonction de Bessel modifiée de première espèce et d'ordre 0. Cette fois-ci, c'est lorsque v = 0 que l'on obtient la Loi de Rayleigh.
Propriétés
Moments
Les premiers moments (non-centrés) sont:
où, Lν(x) représente un Polynôme de Laguerre.
Pour le cas ν = 1/2:
Généralement les moments sont donnés par
où s = σ1/2.
Lorsque k est pair, les moments deviennent des polynômes en σ et ν.
Distributions liées
- La variable
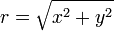 est distribué selon une loi de Rice
est distribué selon une loi de Rice 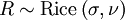 à condition que
à condition que 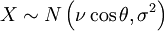 et
et 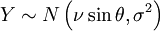 soient deux variables gaussiennes indépendantes.
soient deux variables gaussiennes indépendantes.
- Pour obtenir une variable
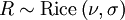 , on peut considérer une autre procédure:
, on peut considérer une autre procédure:
- 1. Tirer P selon une loi de Poisson, de paramètre
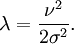
- 2. Tirer X selon une loi du Chi-deux avec 2P + 2 degrés de liberté.
- 3. Poser
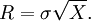
- Si
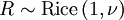 alors R2 possède une distribution Chi-deux non-centré, à 2 degrés de liberté et un paramètre de non-centralité ν2.
alors R2 possède une distribution Chi-deux non-centré, à 2 degrés de liberté et un paramètre de non-centralité ν2.
Cas limites
Pour de grandes valeurs de l'argument, le polynôme de Laguerre devient (voir Abramowitz & Stegun §13.5.1)
On peut constater que lorsque ν devient grand ou que σ devient petit, alors la moyenne devient ν et la variance σ2.
Voir aussi
- Loi de Rayleigh
- Stephen O. Rice (1907–1986)
- Le site SOCR fournit les ressources suivantes: interactive Rice distribution, Rice simulation, model-fitting and parameter estimation.
Références
- Abramowitz, M. and Stegun, I. A. (ed.), Handbook of Mathematical Functions, National Bureau of Standards, 1964; reprinted Dover Publications, 1965. ISBN 0-486-61272-4
- Stephen O. Rice, Mathematical Analysis of Random Noise. Bell System Technical Journal 24 (1945) 46–156.
- I. Soltani Bozchalooi and Ming Liang, A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection, Journal of Sound and Vibration, Volume 308, Issues 1-2, 20 November 2007, Pages 246–267.
- Proakis, J., Digital Communications, McGraw-Hill, 2000.
Lien externe
- MATLAB code for Rice distribtion (densité de probabilité, moyenne, variance et génération de nombres aléatoires)
- Portail des probabilités et des statistiques
Catégorie : Loi de probabilité
Wikimedia Foundation. 2010.

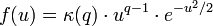
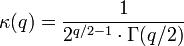
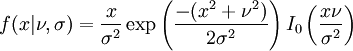
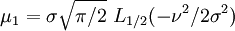
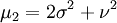
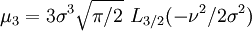
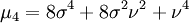
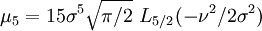
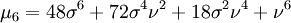
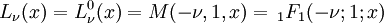
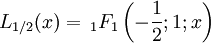
![=e^{x/2} \left[\left(1-x\right)I_0\left(\frac{-x}{2}\right) -xI_1\left(\frac{-x}{2}\right) \right].](/pictures/frwiki/52/485fdacbcff3fdfb33e64d8e66a54da7.png)