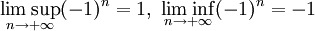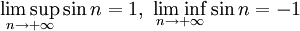- Limite supérieure
-
Limites inférieure et supérieure
En analyse réelle, les limites inférieures et supérieures sont des outils d'étude des suites de nombres réels. Une telle suite n'est en général ni monotone, ni convergente. L'introduction des limites supérieure et inférieure permet de retrouver, partiellement, de telles propriétés. Il s'agit d'un cas particulier de valeurs d'adhérence de la suite.
Sommaire
Définitions
Si
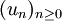 est une suite bornée de réels, les suites définies par
est une suite bornée de réels, les suites définies par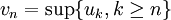 et
et 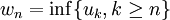
sont respectivement décroissante et croissante. De plus, pour tout n,
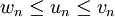 .
.
Ce sont donc des suites convergentes, d'après le théorème de la limite monotone. On pose
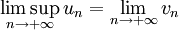 et
et 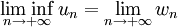 .
.
Ces nombres sont appelés limite supérieure et limite inférieure de la suite
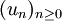 .
.Cette définition s'étend aux suites non nécessairement bornées, en posant
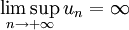 si la suite n'est pas majorée,
si la suite n'est pas majorée,
et
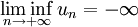 si la suite n'est pas minorée.
si la suite n'est pas minorée.
Exemples
- Pour une suite convergente, la limite supérieure et la limite inférieure sont toutes deux égales à la limite de la suite.
Propriétés
Posons pour alléger les notations
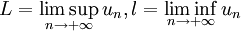 Soit
Soit 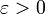 fixé. Alors
fixé. Alors- il n'y a qu'un nombre fini de
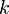 tels que
tels que 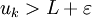 .
.
En effet, la convergence vers
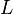 de la suite
de la suite 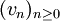 montre que
montre que 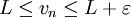 pour
pour  assez grand. Fixons un tel
assez grand. Fixons un tel  . Pour
. Pour 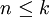 ,
, 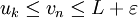 , donc si
, donc si 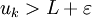 , nécessairement
, nécessairement 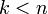
- il y a une infinité de
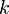 tels que
tels que 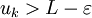 .
.
En effet, pour tout
 ,
, 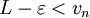 . D'après la définition même de la borne supérieure (plus petit des majorants), il existe
. D'après la définition même de la borne supérieure (plus petit des majorants), il existe 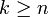 tel que
tel que 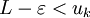 .
.La limite inférieure satisfait a des propriétés analogues. Autrement dit,
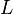 et
et 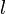 sont respectivement la plus grande et la plus petite des valeurs d'adhérence de la suite
sont respectivement la plus grande et la plus petite des valeurs d'adhérence de la suite 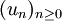 . Notons au passage que l'existence de
. Notons au passage que l'existence de 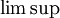 et
et 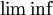 pour une suite bornée fournit une preuve du théorème de Bolzano-Weierstrass
pour une suite bornée fournit une preuve du théorème de Bolzano-WeierstrassApplication : formule de Hadamard
La formule de Hadamard donne l'expression du rayon de convergence
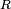 d'une série entière
d'une série entière 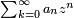 en termes d'une limite supérieure :
en termes d'une limite supérieure :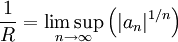 .
.
Cette formule découle de l'application de la règle de Cauchy.
Généralisations
Nombres dérivés
D'une manière analogue, si
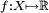 est une fonction numérique définie sur un espace topologique, on peut définir
est une fonction numérique définie sur un espace topologique, on peut définir 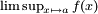 . Cela permet par exemple de définir les nombres dérivés d'une fonction
. Cela permet par exemple de définir les nombres dérivés d'une fonction 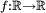 . Ce sont les nombres
. Ce sont les nombres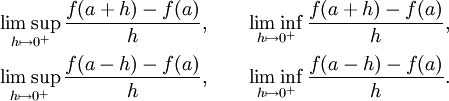
(attention : comme ci-dessus, ces limites peuvent valoir
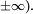
Limites inférieure et supérieure d'une suite de parties d'un ensemble
On peut aussi définir
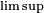 et
et 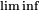 pour une suite
pour une suite 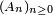 de parties d'un ensemble, en posant
de parties d'un ensemble, en posant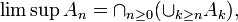
et
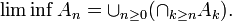
On interprète
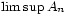 comme l'ensemble des
comme l'ensemble des 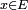 qui appartiennent à
qui appartiennent à 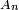 pour une infinité d'indices
pour une infinité d'indices  , et
, et 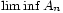 comme l'ensemble des
comme l'ensemble des 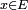 qui appartiennent à tous les
qui appartiennent à tous les 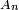 à partir d'un certain rang. Ces notions jouent un rôle important en calcul des probabilités, dans la démonstration de la loi forte des grands nombres. Voir par exemple le lemme de Borel-Cantelli.
à partir d'un certain rang. Ces notions jouent un rôle important en calcul des probabilités, dans la démonstration de la loi forte des grands nombres. Voir par exemple le lemme de Borel-Cantelli.Liens internes
- Portail des mathématiques
Catégories : Analyse réelle | Suite
Wikimedia Foundation. 2010.