Theoreme de la limite monotone

Theoreme de la limite monotone

Théorème de la limite monotone

Sommaire

Énoncé pour les fonctions

Soient \ ]a,\, b[ un intervalle ouvert (borné ou non) et une fonction croissante \ f :\, ]a,\, b[\, \to \R. Alors :

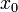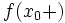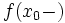  • la fonction admet en tout point \ x_0 une limite à droite et une limite à gauche, qu'on note respectivement \ f(x_0+) et \ f(x_0-) ; elles vérifient la double inégalité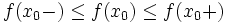 \ f(x_0-) \leq f(x_0) \leq f(x_0+)
  • la fonction admet à la borne de droite de l'intervalle une limite, finie ou non ; cette limite est finie si et seulement si 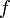\ f est majorée, et dans le cas contraire est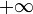 \ +\infty
  • la fonction admet à la borne de gauche de l'intervalle une limite, finie ou non ; cette limite est finie si et seulement si 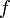\ f est minorée, et dans le cas contraire est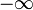 \ -\infty
(théorème analogue pour les fonctions décroissantes ; il se déduit immédiatement du précédent en remplaçant 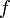\ f par \ -f ).


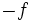Démonstration

Montrons le résultat en b, les autres cas s'en déduisent immédiatement. Si f\left(\left]a,b\right[\right) est majoré alors d'après la propriété de la borne supérieure il admet une borne supérieure qu'on notera l. 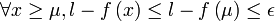Par définition le la borne supérieure : \forall\epsilon\in\mathbb{R}_{+}^{*},\exists\mu\in\left]a,b\right[,l-f\left(\mu\right)\leq\epsilon or f est croissante donc pour ε fixé et μ donné \forall x\geq\mu,l-f\left(x\right)\leq l-f\left(\mu\right)\leq\epsilon. Ce qui montre que f admet l pour limite en b

Énoncé pour les suites

Soit 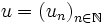u=\left(u_n\right)_{n\in\mathbb{N}} une suite réelle croissante.

  • Si la suite est majorée alors elle est convergente.
  • Si la suite n'est pas majorée alors elle admet 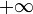\ +\infty pour limite.
(théorème analogue pour les suites décroissantes ; il se déduit immédiatement du précédent en remplaçant 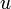\ u par \ -u ).



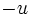Démonstration

La démonstration est analogue à la démonstration dans le cas des fonctions.

Liens internes

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de la limite monotone ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de la limite monotone de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Théorème de la limite monotone — Le théorème de la limite monotone est un théorème d analyse, la branche des mathématiques qui est constituée du calcul différentiel et intégral et des domaines associés. Sommaire 1 Énoncé pour les fonctions 2 Énoncé pour les suites 3 …   Wikipédia en Français

  • Théorème de la bijection — En analyse réelle, le théorème de la bijection est un corollaire du théorème des valeurs intermédiaires, affirmant qu une fonction continue et strictement monotone sur un intervalle constitue une bijection entre cet intervalle et son image. Cette …   Wikipédia en Français

  • Limite inférieure — Limites inférieure et supérieure Exemple de recherche de limites inférieure et supérieure. La suite xn est représentée en bleu. En analyse réelle, les limites inférieures et supérieures sont des outils d étude des suites de nombres réels. Une… …   Wikipédia en Français

  • Limite supérieure — Limites inférieure et supérieure Exemple de recherche de limites inférieure et supérieure. La suite xn est représentée en bleu. En analyse réelle, les limites inférieures et supérieures sont des outils d étude des suites de nombres réels. Une… …   Wikipédia en Français

  • Theoreme de convergence monotone — Théorème de convergence monotone En mathématiques, le Théorème de convergence monotone est l un des théorèmes importants de la théorie des intégrales au sens de Lebesgue avec le théorème de convergence dominée. Ce théorème indique que la… …   Wikipédia en Français

  • Théorème de Beppo-Levi — Théorème de convergence monotone En mathématiques, le Théorème de convergence monotone est l un des théorèmes importants de la théorie des intégrales au sens de Lebesgue avec le théorème de convergence dominée. Ce théorème indique que la… …   Wikipédia en Français

  • Théorème de convergence monotone — En mathématiques, le théorème de convergence monotone, ou théorème de Beppo Levi, est l un des théorèmes importants de la théorie des intégrales au sens de Lebesgue avec le théorème de convergence dominée, qui s en déduit. Ce théorème indique que …   Wikipédia en Français

  • Théorème de Dini — Théorèmes de Dini En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 28 octobre 1918) …   Wikipédia en Français

  • Fonction Monotone — Dans l étude des fonctions numériques à valeurs dans , les fonctions monotones tiennent une grande place. Ce sont les fonctions dont le sens de variation ne change pas. Une fonction monotone sur un intervalle I est une fonction qui reste… …   Wikipédia en Français

  • Fonction monotone — Dans l étude des fonctions numériques à valeurs dans ℝ, les fonctions monotones tiennent une grande place. Ce sont les fonctions dont le sens de variation ne change pas. Une fonction monotone sur un intervalle est une fonction qui reste… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”