Limite semi-classique

Le régime semi-classique d'un système physique en mécanique quantique est le régime pour lequel les actions du système physique étudié sont grandes devant le quantum d'action 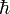. Mathématiquement, cela revient à effectuer un développement asymptotique des grandeurs quantiques au voisinage de .

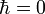L'étude du régime semi-classique est en général non-triviale, car la limite 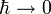de la mécanique quantique est singulière au sens de la théorie des perturbations. Pour illustrer ce point, considérons par exemple une particule non relativiste de masse m soumise à une force conservative dérivant de l'énergie potentielle 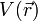. La recherche des états propres de l'énergie passe par la résolution de l'équation de Schrödinger indépendante du temps :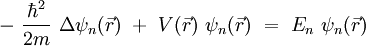

dont la limite 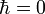est singulière, car ce n'est plus une équation aux dérivées partielles.

Articles liés

• Approximation BKW
• Quantification semi-classique
• Formule des traces de Gutzwiller
• Théorie des perturbations
• Géométrie spectrale
• Opérateur pseudo-différentiel
• Opérateur Fourier intégral
• Analyse micro-locale

Bibliographie

Revues générales

• Michael Berry & K. Mount, Semiclassical approximations in wave mechanics, Report on Progress in Physics 35 (1972), 315-397. pdf.
• Michael Berry ; Some quantum-to-classical asymptotics, dans : Chaos & Quantum Physics, Les Houches Lecture Series LII eds. M-J Giannoni, A Voros and J Zinn-Justin, North-Holland (1989), 251-304. pdf.
• André Voros ; Aspects de la limite (semi)-classique, Journées X-UPS 5 (1987/1988), 37-48. pdf.
• André Voros ; Semi-classical approximations, Annales de l'institut Henri Poincaré A 24 (1) (1976), 31-90. Numdam.

Aspects mathématiques

• Bernard Helffer ; 30 ans d'analyse semi-classique : bibliographie commentée (essai inachevé) (2003). PostScript.
• Didier Robert ; Semi-classical approximation in quantum mechanics. A survey of old and recent mathematical results, Helvetica Physica Acta 71 (1) (1997), 44-116.
• André Martinez ; An Introduction to Semiclassical and Microlocal Analysis, Springer-Verlag (2002), ISBN 0387953442.
• Didier Robert ; Autour de l'approximation semi-classique, Progress in Mathematics 68, Birkhäuser (1987), ISBN .
• Bernard Helffer ; Introduction to the semi-classical Analysis for the Schrödinger operator and applications, Lecture Notes in Mathematics 1336, Springer-Verlag (1986).
• V. Maslov ; Théorie des Perturbations, Dunod (1972).
• Bernard Helffer, André Martinez et Didier Robert ; Ergodicité et limite semi-classique, Communication in Mathematical Physics 109 (1987), 313-326.
• Bernard Helffer ; h-pseudodifferential operators and applications: an introduction, Tutorial lectures in Minneapolis. The IMA Volumes in Mathematics and its applications 95 Quasiclassical Methods, Springer Verlag (1997), 1-50.
• Mouez Dimassi & J. Sjostrand ; Spectral Asymptotics in the Semi-Classical Limit, Cambridge University Press (1999), ISBN 0521665442.

• Portail des mathématiques
• Portail de la physique