Jet sans limite

Cet article fait partie de la série

Jeu de rôle

Jeux : Liste par genre • Catégories par genre • Liste alphabétique • Autres : Éditeurs • Magazines

Univers

Science-fiction • Fantasy et fantastique • Mondes de fiction

Systèmes et Mécanismes

Systèmes • Mécanismes • Scénario • Rôle (jeu d'acteur) • Probabilités des dés • Jeu de rôle psychologique

Jargon

Meneur de jeu • Personnage joueur • Personnage non-joueur • Lexique

Voir aussi

Jeu d'aventure • (jeu vidéo) • Grandeur nature (semi-réel) • Jeu de cartes à collectionner • Jeu de société • Jeu à rôles • MMORPG • Jeu de figurines • Livre-jeu • Murder party • Jeu de guerre

Méta

Portail • Projet Participez !

Les jeux de rôle sur table utilisent en général des dés pour introduire le hasard. Ceci est un élément important du suspense, les événements n'étant pas sûrs. De plus, on ne peut pas permettre au meneur de jeu de décider de la victoire et de la vie des personnages en cas de combat ; on a donc recours à ce mécanisme pour introduire un peu d'impartialité.

Dans bien des cas, il s'agit pour le joueur d'un jeu de rôle d'effectuer un jet de dé, charge au maître du jeu d'interpréter le tirage en termes de réussite ou d'échec de l'action entreprise par le joueur. Les différents jeux existants utilisent différentes règles à cette fin.

Les jets de dés

Normalement, le jet d'un dé donne des valeurs allant de 1 au nombre de faces, par exemple, un dé à six faces (dé classique, noté « d6 ») donne des valeurs comprises entre 1 et 6, tandis qu'un dé à vingt faces (d20) donne des valeurs entre 1 et 20.

Si on lance plusieurs dés identiques, alors la plage va du nombre de dé(s) à la somme du nombre de faces ; par exemple si on lance deux dés à six faces (noté « 2d6 »), la plage de valeurs est 2–12, et pour 3d6, la plage est 3–18.

On utilise souvent deux dés à dix faces (d10) pour avoir un pourcentage (nombre compris entre 1 et 100, souvent désigné comme un d100 ou parfois d%) :

• soit le joueur n'a qu'un seul dé ; le premier jet indique le chiffre des dizaines, le second le chiffre des unités ;
• soit le joueur a deux dés que l'on peut distinguer (couleur ou taille différentes) ; il désigne un des deux dés comme celui des « dizaines » (l'autre devenant le dé « unitaire »).

Deux zéros se lisent comme un 100. Il existe un dé ayant réellement cent faces, mais qui est peu utilisé — les faces faisant un angle faible entre elles, il a une propension à rouler sans s'arrêter — et reste une curiosité.

Jet sans limite

Le jet sans limite (JSL) (anglais : open-ended die, littéralement jet à fin ouverte ) est un mécanisme de jeu de rôle permettant d'étendre la plage de valeurs données par un jet de dé(s).

Lorsque l'on obtient un des extrêmes de la plage, on relance les dés ; le résultat est alors ajouté au résultat précédent si le premier jet était maximal, retranché si le jet était minimal. Ce mécanisme est récursif, ce qui explique le terme de « sans limite ».

Exemple avec 1d20 :

Si le jet donne un résultat entre 2 et 19, je garde le résultat tel quel.

Si le résultat est un 20, je retire un d20 et le résultat est ajouté à ce 20 ; si le deuxième jet est un 20 (on a donc 40 pour l'instant), je tire un troisième dé que j'ajoute…

Si le premier résultat est un 1, je retire un d20 et le résultat est déduit de ce 1 ; si le deuxième jet est un 20 (on a donc -19 pour l'instant), je tire un troisième dé que je retranche…

Les deux principaux jeux utilisant ce système sont Rolemaster et le Jeu de rôle des Terres du Milieu.

On notera en outre que par exemple Star Wars (d6) applique ce système à un des dés à six faces lancés ; dans un autre registre, Anima permet les jets ouverts sur des dés à cent faces : il est donc possible d'obtenir des résultats allant dans les 300, 400... Ce qui permet des actions a priori physiquement impossibles.

Utilisation dans Rolemaster

Le système de Rolemaster utilise exclusivement des d100.

La plupart des jets sont des jets sans limite, également appelés jets de dés « ouverts » (open ended).

Le principe en est simple :

Réussite critique

(ou Jet sans limite positif) Sur un jet de d100 dans la plage de 96-100, on relance le dé et on ajoute le résultat. Tant que l'on réussit dans cette plage, on retire pour aboutir au jet final.

Exemple : 98 ; je retire (100), total temporaire = 198 mais je viens de faire un 100 donc je retire (45) pour aboutir à un total final de : 243. Du fait que j'ai fait 45, on ne retire pas de jet supplémentaire.

Échec critique

(ou Jet sans limite négatif) Même principe qu'au-dessus sauf que l'on soustrait le résultat au jet. La plage de critique est de 01-05 seulement pour le premier jet. La plage d'échec critique pour les jets suivants est dans la tranche des 96-100. On retire tant que l'on fait des jets dans cette dernière plage.

Exemple : 4, je relance (96), total temporaire = -92 mais je viens de faire un 96 donc je retire (100 à nouveau), total temporaire = -192. Je retire encore (3) pour aboutir à un total final de : -195.

Utilisation des jets de dé

Le jet de dé est en général comparé à un seuil ; une action donne un effet si le jet est au-dessus de ce seuil, et un autre effet si le jet est en dessous.

Par exemple, on peut avoir une table donnant le temps qu'il fait ; selon le résultat du jet de dé, la table indique s'il pleut, s'il fait beau, s'il y a du vent…

Lorsqu'un personnage tente une action incertaine, c'est le jet de dé qui indique si l'action échoue ou réussit, en général en prenant en compte la difficulté de l'action et la compétence du personnage.

Voir l'article détaillé Systèmes de jeux de rôle.

Un peu de probabilité…

Différence entre 1d20, 2d10 et 3d6

On pourrait résumer la question par : « le résultat d'un dé à vingt faces (1d20) est-il équivalent à la somme de deux dés à dix faces (2d10) ou de trois dés à six faces (3d6) ? » La réponse est évidemment non. Mais il ne faut pas croire que la seule différence est l'intervalle couvert par le résultat, ce que pouvait laisser à penser la première notation qui a existé (celle de Donjons & Dragons 1^re édition) : 1d20 était noté « 1–20 », 2d10 était noté « 2–20 » et 3d6 était noté « 3–18 ».

Il faut en fait considérer la notion de dénombrement, utilisée en probabilité (mathématiques). Il faut compter le nombre d'évènements, c'est-à-dire le nombre de manières que l'on a d'obtenir un résultat (ou encore le nombre de positions des dés donnant ce résultat).

Avec 1d20, chaque nombre ne peut être fait que d'une seule manière, avec une seule position du dé. Chaque position ayant la même probabilité d'apparaître, chaque nombre a donc une probabilté de 1/20 (soit 5 %) de sortir.

Avec 2d10, on a cent possibilités, cent positions possibles des deux dés :

probabilités comparées d'avoir un résultat avec 1d20, 2d10 et 3d6

On voit que si l'on n'a qu'une seule manière (soit une chance sur cent, 1 %) d'obtenir 2 (1+1) ou 20 (10+10), on a deux manières (soit 2 %) d'obtenir 3 (1+2 ou 2+1), trois manières (soit 3 %) d'obtenir 4 (1+3, 2+2 et 3+1)… et neuf manières (soit 9 %) d'obtenir 10 (1+9, 2+8, 3+7, 4+6, 5+5, 6+4, 7+3, 8+2, 9+1). On peut faire le même calcul avec 3d6 : il y a 216 combinaisons possibles mais une seule manière (soit 0,46 %) d'obtenir 3 (1+1+1), trois manières (1,38 %) d'obtenir 4 (2+1+1, 1+2+1, 1+1+2)…

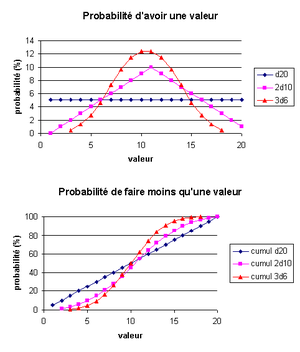
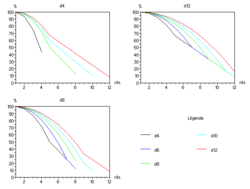
Maintenant, on prend une valeur v, par exemple 5, et l'on veut savoir combien on a de chances de faire cette valeur ou moins que cette valeur — c'est ce qui se passe lorsque l'on fait un « jet sous une compétence ». On réussit si l'on fait 1, 2, 3, 4 ou 5 ; il faut donc sommer, cumuler les probabilités. Avec 1d20, on a 5 × 5 % = 25 % de chances de réussite ; avec 2d10, on a 1 + 2 + 3 + 4 = 10 % de chance de réussite. Ceci est synthétisé sur la figure ci-contre.

Lorsque l'on jette 3d6, on a plus de chances d'obtenir un score moyen (environ 10) qu'avec 2d10 ; et avec 1d20, un score moyen n'est pas plus favorisé qu'un autre. Donc, si l'on tire les caractéristiques aux dés, plus on additionne de dés, plus on aura de chance d'avoir une caractéristique moyennne, rares seront les personnages avec une caractéristique haute ou basse. Avec un seul dé, on aura autant de chances d'avoir une caractéristique basse que haute ou moyenne.

Si l'on considère un jet sous une capacité (ou au-dessus d'une capacité), on voit qu'en utilisant 2d10 au lieu de 1d20, pour un référentiel de niveaux de difficulté donné, on défavorise les personnages faibles (un personnage ayant une capacité en dessous de 11 a moins de chances de réussir l'action avec 2d10 qu'avec 1d20) ; par contre, cela favorise les personnages forts ; ceci s'accentue encore plus en utilisant 3d6. Il est cependant possible d'adapter le référentiel des niveaux de difficulté de manière à retrouver les mêmes probabilités quel que soit le système choisi.

Il ne s'agit pas de dire qu'un système est meilleur que l'autre : d'une part l'approche du réel par des nombres est nécessairement très imparfaite, un système n'est pas plus réaliste qu'un autre (par contre, il peut être plus jouable) ; d'autre part, ce n'est pas la règle en elle-même qui est importante (à partir du moment ou elle permet une bonne fluidité de jeu), mais surtout le fait qu'elle s'applique à tout le monde.

Choix de certains dés parmi plusieurs (roll & keep)

Probabilité d'avoir un score en jetant trois dés, et en jetant quatre dés et en sommant les trois meilleurs

Dans certains systèmes, lors de la création des personnages, on jette quatre dés à six faces et on retient les trois meilleures. De fait, les résultats obtenus sont meillleurs que si l'on jetait 3d6. Les courbes de probabilité sont représentées ci-contre.

Probabilités en sommant deux dés choisis (les plus mauvais ou les meilleurs) parmi n
Probabilité d'avoir un score (haut) et probabilité d'atteindre ou de dépasser un score (bas)

Dans le jeu de rôle P'tites sorcières, on somme deux dés à six faces, mais selon la puissance du personnage, il s'agit

• des deux pires dés parmi trois ou quatre (personnage faible) ;
• simplement de deux dés (personnage moyen) ;
• des deux meilleurs dés parmi trois ou quatre (personnage fort).

Voir également ci-dessous Dépasser un seuil avec au moins un dé parmi n.

Jet sans limite

Probabilité d'obtenir une valeur avec un jet sans limite d'un d20

Considérons un jet sans limite avec un dé à vingt faces.

Certaines valeurs ne peuvent pas sortir : évidemment 1 et 20, puisqu'un premier jet donnant 1 ou 20 est nécessairement modifié. On a 5 % ((1/20)×100 %) de chances d'obtenir chaque valeur entre 2 et 19, 5 % d'obtenir une valeur nulle ou négative, 5 % d'obtenir une valeur supérieure à 20.

Dans le cas d'un second jet, chaque valeur a 5 % de chances de sortir, soit une probabilité totale de 0,25 % ((1/20)²×100 %). De manière récursive, on en déduit que :

• pour les valeurs inférieures ou égales à 1,
  • les valeurs de la forme (1-20·k) ont une probabilité nulle (k étant un nombre entier positif ou nul) ;
  • les valeurs entre (1-20·(k+1)) et (1-20·k) ont une probabilité 0,05^k+2×100 % de sortir ;
• pour les valeurs strictement supérieures à 1,
  • les valeurs de la forme 20·k ont une probabilité nulle (k étant un entier strictement positif) ;
  • les valeurs entre 20·k et 20·(k+1) ont une probabilité 0,05^k+1×100 % de sortir.

Ceci est à comparer avec la probabilité d'1d20 simple : 5 % d'obtenir chaque valeur entre 1 et 20.

On a donc la table de probabilités suivante, entre -50 et 50 :

Probabilité de dépasser un seuil avec un jet sans limite d'un d20

Si l'on considère la probabilité de dépasser un seuil (il s'agit de l'intégrale de la courbe précédente), on constate donc que :

• sur une tranche de dix-neuf valeurs, la pente est constante ;
• toutes les vingt valeurs, on a un plateau horizontal.

La moyenne du jet sans limite est de 10,4 contre 10,5 pour un jet de d20 normal.

Avec un dé à cent faces, en rejouant les score 1–5 et 96–00, on obtient un profil similaire. Les valeurs interdites sont : …, -95, 5, 96, 196, …

Les valeurs entre 6 et 95 ont 1 % de chances de sortir. Pour avoir une valeur entre 101 et 191, il faut obtenir un 1–5 au premier jet ; il existe 5 combinaisons possible par valeur (par exemple pour 110 : 96+14, 97+13, 98+12, 99+11, 00+10), soit 0,05 % de chances d'obtenir ce score (chaque combinaison ayant 0,01² soit 0,01 % de chances de sortir).

Entre 96 et 101, les probabilité croissent de manière linéaire de 0 à 0,05 % de chances :

• on ne peut jamais obtenir 96 (puisque le 96 est rejoué) ;
• le 97 peut s'obtenir avec une seule combinaison : 96+01, soit 0,01 % de chances ;
• le 98 peut s'obtenir de deux manières : 96+02 et 97+01, soit 0,02 % de chances ;
• …

De la même manière, les probabilités entre 191 et 196, les chances passent linéairement de 0,05 % à 0.

Pour les échecs critiques, le calcul est similaire :

• des scores entre 5 et 0, on passe linéairement de 0 à 0,05 % de chances ;
• entre 0 et -90, les chances sont de 0,05 % ;
• entre -90 et -95, les chances passent linéairement de 0,05 % à 0.

Nombre de dés variable

Dans certains jeux, le nombre de dés à jeter varie en fonction de la difficulté de l'action ou bien de la capacité du personnage.

Dépasser un seuil avec la somme des dés

probabilités comparées d'avoir un résultat avec nd6

Dans certains jeux (La Guerre des étoiles 1^e éd., D6 System, Le Livre des cinq anneaux), la capacité du personnage à résoudre une action est donnée par un nombre de dés, le seuil à franchir étant un nombre fixe représentant la difficulté de l'action ; par exemple un personnage peu doué aura 1d6 et un personnage très doué aura 5d6, et un seuil de difficulté moyen est 9. Ou alors (RuneQuest, Avant Charlemagne, Empire galactique, Trauma), la difficulté est représentée par un nombre de dés, et la capacité d'un personnage est un nombre fixe ; par exemple, un personnage moyen a une capacité de 9, une action simple se joue à 1d6 et une action complexe à 5d6. On peut faire les mêmes calculs que précédemment, les résultats sont présentés sur la figure ci-dessous.

Nous avons représenté sur la figure du bas la probabilité de faire moins qu'une valeur :

• si le nombre de dés représente la difficulté et qu'il faut faire moins qu'un seuil, alors une courbe donnée représente les chances de réussite pour une difficulté donnée (nombre de dés) en fonction du score de la capacité (seuil) ;
• si le nombre de dés représente la capacité et qu'il faut faire au-delà d'un seuil, alors une courbe correspond aux probabilités d'échec pour une capacité fixée (nombre de dés) en fonction de la difficulté (seuil).

Probabilité de dépasser un score donné avec nd6

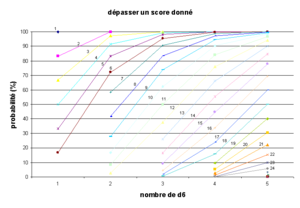
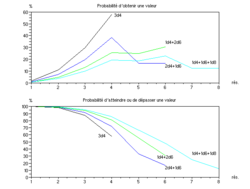
Nous représentons ci-dessous les résultats d'une manière différente : on regarde l'évolution de la probabilité de dépasser un seuil donné en fonction du nombre de dés ; le seuil est le nombre indiqué à côté de la courbe. Chaque courbe représente les chances de réussite d'une action de difficulté donnée (le seuil est fixé) en fonction de la puissance du personnage (nombre de dés).

Par exemple, le score « 1 » ne peut s'obtenir qu'avec 1d6, et l'on fait obligatoirement 1 ou plus ; « 1 » est donc représenté par un point unique (1d6,100%) de couleur bleu marine. La probabilité de faire 6 ou plus passe de 16,67 % avec 1d6 à 99,99 % avec 5d6 (courbe marron). Un seuil de 18 ne peut pas être atteint avec 1 ou 2d6 ; les probabilités de réussite passent de 0,46 % avec 3d6 à 50 % avec 5d6 (courbe bleu ciel).

Dépasser un seuil avec au moins un dé parmi n

probabilité de dépasser un seuil donné avec 1d6 parmi n

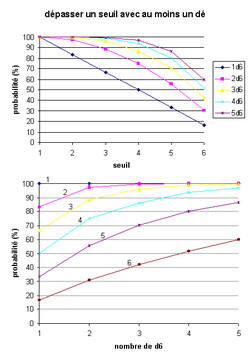
Dans certains jeux (Shadowrun, jeux du Monde des ténèbres, comme Vampire : la Mascarade), la capacité à réussir l'action est également exprimée par un nombre de dés, mais on ne fait pas la somme des dés : on fixe un seuil dans la gamme de valeurs d'un dé (par exemple entre 1 et 6 pour des d6), et l'action est réussie si au moins un dé atteint ou dépasse cette valeur. Bien évidemment, plus le joueur jette de dés, plus il a de chance de réussir au moins un jet.

Dans certains cas, le nombre de dés dépassant le seuil donne la qualité de la réussite.

On voit qu'avec ce système, les personnages puissants (ayant un grand nombre de dés) sont surtout favorisés pour les hauts seuils : ils n'ont pas tellement plus de chance de réussir les actions faciles que les personnages faibles, mais réussissent bien mieux les actions difficiles.

Probabilité d'avoir une valeur en choisissant la plus haute parmi avec deux dés différents

Dans certains jeux (par exemple Usagi Yojimbo), on jette deux ou plusieurs dés pouvant être différents (par exemple 1d4 et 1d6), et on ne retient que la plus haute valeur. Si les deux dés sont identiques (même nombre de faces n), il y a n² combinaisons possibles :

• la valeur « 1 » n'a qu'une seule chance de sortir (1 et 1), soit une probabilité 1/n ² ;
• la valeur la plus haute n a 2n-1 possibilités de sortir (un des dés est indique n, l'autre peut prendre toutes les valeurs possibles), la probabilité est donc (2n-1)/n ² ;
• entre ces deux valeurs, la probabilité croît linéairement (pour une valeur i, un des dés doit avoir la valeur i et l'autre une valeur inférieure ou égale à i).

Si les dés n'ont pas le même nombre de faces, n₁ et n₂ (n₁ < n₂) :

• de 1 à n₁, on a comme ci-dessus un comportement linéairement croissant ;
• entre n₁+1 et n₂, seul compte le score du dé ayant le plus de faces, on a donc une probabilité uniforme valant 1/n₂.

La probabilité d'atteindre ou de dépasser un score est la somme des probabilités pour les valeurs supérieures ou égalees à ce score. On a donc logiquement (intégrales classiques en mathématiques) :

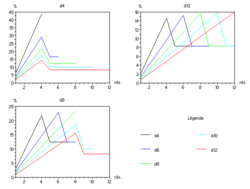
• une branche de parabole sur la partie où la probabilité croît linéairement :
• un segment de droite sur la partie où la probabilité est constante ;
• une rupture de pente entre les deux, correspondant à la discontinuité dans la progression des probabilités.

La figure ci-contre montre les probabilités lorsque l'on a trois dés, pouvant être différents.

On peut classer les combinaisons de dé par ordre de moyenne croissante.

Statistiques des sommes de dés

pour un dé régulier : la moyenne s'obtient simplement comme la moitié de la somme du minimum et du maximum. Exemple : la moyenne d'un dé cubique classique (à six faces de 1 à 6), la moyenne est de (1+6)/2 = 3,5 ; pour un dé à dix faces, la moyenne est de 5,5. Si le dé n'est pas régulier (par exemple : le dé doubleur du backgammon, qui porte les points 2 - 4 - 8 - 16 - 32 - 64) il faut calculer la moyenne (somme des points divisées par le nombre de faces (dans l'exemple, 126/6 = 21)

pour plusieurs dés : C'est une règle mathématique universelle que, pour des séries indépendantes, les moyennes, les minimums, et les maximums s'additionnent respectivement, et cela s'applique aux dés, quel que soit leur nombre. Par exemple, pour un dé à six face et un dé à dix faces, la moyenne est la somme des moyennes de (3,5 + 5,5 = 9), le minimum est la somme des minimums (1+1 = 2) et le maximum la somme des maximums (6 + 10 = 16). Si les dés sont réguliers, la moyenne s'obtient toujours comme demi-somme du maximum et du minimum ( (2 + 16)/2 = 9).

le mode est la valeur, ou le groupe de valeurs, qui ont la probabilité la plus importante.

• pour un dé, toutes les valeurs sont équiprobable et le mode couvre toute la plage de valeur (par exemple : la plage de 1 à 6 pour le dé classique)
• pour la somme de deux dés réguliers, le mode est la plage de valeur comprise entre le maximum du plus petit dé + le minimum du plus grand, et le maximum du plus grand dé + le minimum du petit grand (par exemple : pour 1D4 + 1D10, entre 4+1 et 1+10). Toutes les valeurs du mode ont la même probabilité, avec un nombre de cas égale au nombre de face du plus petit dé (dans l'exemple, il y a toujours 4 façons sur 40 de faire 5, 6, 7, 8, 9, 10 et 11). Pour deux dés identiques, la règle s'applique mais le mode se réduit à une seule valeur (entre 1+6 et 6+1 pour deux dés classique, c'est-à-dire 7 ; qui s'obtient de 6 façons différentes)
• pour trois dés et plus, le mode se réduit à la moyenne (exemple : 14 pour 4 dés), ou aux deux valeurs entières qui l'encadrent (exemple : 10 et 11 pour trois dés, situation où la moyenne est 10,5)

Nota :

1. un ajustement fixe ("+1" dans un calcul "1D6 +1") est parfaitement équivalent à un dé à une seule face portant ce chiffre, et que donc on peut appliquer toutes les règles qui précèdent : la moyenne d'1D6 +1 est de 3,5 + 1 = 4,5 etc.
2. une différence entre des dés est parfaitement équivalente à l'addition d'un dé négatif. Par conséquent les règles continuent à s'appliquer

Jeux n'utilisant pas de dés

Il existe quelques rares jeux de rôle n'utilisant pas de dés. On peut citer Prince Valiant, qui utilise des pièces de monnaies (pile ou face), ou encore Ambre, qui se joue sans aucun recours au hasard chiffré (ni dés, ni cartes, ni pièces). Dans ce dernier cas, on se contente de comparer les traits : "le plus fort gagne", ou bien, en cas d'égalité trop sensible, c'est le plus rusé qui l'emporte.

Il y a aussi des jeux qui n'utilisent pas de dés, mais qui les remplacent par des cartes à jouer ; si les probabilités en sont changées, le mécanisme n'est pas fondamentalement différent. La plus grosse différence est que, souvent, le joueur peut décider de la carte qu'il joue selon ce qu'il a en main, ce qui lui donne plus de contrôle sur la destinée de son personnage. Les jeux les plus renommés dans cette catégorie sont Château Falkenstein et Miles Christi. Deadlands et les jeux qui en sont issus (la gamme Savage Worlds) mêlent dés et cartes.

Certains jeux utilisent des cartes de Tarot, notamment Ambre et Chimères ; servant avant tout d'aides à la créativité, elles peuvent aussi partiellement remplacer les dés.