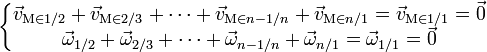Isostatisme, hypostatisme et hyperstatisme

En mécanique des solides, l'isostatisme est la situation d'un assemblage pour lequel le fonctionnement se fait sans contrainte excessive ou pour être plus rigoureux si le principe fondamental de la dynamique suffit à déterminer toutes les inconnues de liaisons du mécanisme.

On assemble des pièces afin de réaliser une ou plusieurs fonctions. Une des fonctions peut consister à être une structure immobile (bâtiment, pont, …), ou bien à réaliser un travail (par exemple déplacer une charge). Dans tous les cas, chaque pièce est en contact avec plusieurs autres, ce qui va d'une part limiter les mouvements de chaque pièce, et d'autre part permettre la transmission d'efforts.

Ainsi, la mobilité d'une pièce d'un assemblage est nécessairement limitée ; certains degrés de mobilité sont supprimés, mais chaque degré de mobilité n'est supprimé qu'une seule fois.

Lorsque l'assemblage possède trop de mobilités, on parle d'hypostatisme. D'un point de vue mécanique, au moins une pièce conserve au moins une possibilité de mouvement (au moins un degré de mobilité) qui est nuisible au fonctionnement. Si c'est un mécanisme, il va présenter des instabilités, des mouvements parasites ; si c'est une structure métallique, elle ne tiendra pas.

On parle d'hyperstatisme lorsque les pièces subissent plus de contraintes que ce qui est strictement nécessaire pour les maintenir ; au moins un degré de mobilité d'une pièce est supprimé plusieurs fois.

Sommaire 1 Mobilité d'une pièce 2 Gestion de l'hyperstatisme 3 Point de vue mathématiques 3.1 Étude statique 3.2 Étude cinématique 4 Détermination de l'isostatisme 4.1 Positionnement isostatique d'une pièce à usiner 4.2 Cas des structures métalliques 4.3 Cas des mécanismes 4.3.1 Exemple du système manivelle-bielle-piston 5 Calcul des structures élastiques hyperstatiques 5.1 Poutre encastrée-appuyée sollicitée en son centre 6 Autre contexte d'utilisation 6.1 Gestion de production 6.2 Lors d'une étude de mouvement avec un logiciel de conception (COSMOSMotion par exemple) 7 Voir aussi 7.1 Articles connexes 7.2 Liens externes 7.3 Bibliographie 7.4 Notes et références

Mobilité d'une pièce

Dans un assemblage — mécanisme ou structure —, les pièces sont liées entre elles. Une pièce sans aucune liaison peut se déplacer librement dans l'espace ; on décompose le mouvement en translations selon les trois axes de référence du repère, x, y, et z, et en rotations selon les trois mêmes axes. Une pièce libre peut bouger selon ces 6 mouvements, on dit qu'elle a 6 degrés de mobilité.

Dans le mécanisme ou la structure, la pièce est en contact avec d'autres pièces. Ces contacts vont l'empêcher de bouger, ils vont réduire la mobilité de la pièce, ils « suppriment des degrés de liberté » ; cela est modélisé par la notion de liaison.

Si aucune pièce ne peut bouger, on dit que le système est statique, et l'on distingue deux cas :

• l'isostatisme : les contacts sont juste suffisants pour maintenir l'immobilité ;
• l'hyperstatisme : il y a plus de contacts que nécessaire.

Prenons l'exemple de la stabilité d'une table (il ne s'agit pas d'un exemple d'isostatisme puisque l'on peut faire bouger la table : il est donné pour illustrer la notion de contraintes juste suffisantes). On considère le système formé par la table et le sol :

• si la table n'a que deux pieds, elle ne peut pas être stable, elle va pivoter et tomber, le système est instable ;
• si la table a trois pieds non alignés (disposés en triangle), elle est stable ; une table à trois pieds n'est jamais bancale^[1] ;
• si la table a quatre pieds, elle est stable si tout est parfait (sol plan, plateau de la table plan et pieds de la même longueur) ; le quatrième pied est une contrainte supplémentaire.

Dans la réalité, rien n'est strictement parfait, la table à quatre pieds risque d'être bancale^[2]. Si l'on visse les quatre pieds au sol, le plateau de la table va se déformer pour s'adapter aux défaut, alors qu'avec une table à trois pieds, le plateau ne va pas se déformer.

Prenons maintenant l'exemple d'une plaque fixée à un mur. La plaque est en appui plan sur le mur, ce qui laisse trois degrés de mobilité : les deux translations dans le plan du mur et la rotation dans ce même plan (autour d'un axe perpendiculaire au mur). Si l'on se contente de mettre une seule vis, on ajoute une liaison pivot ; on bloque les translations, mais il reste la rotation, on conserve un degré de mobilité. Pour empêcher la plaque de tourner, on peut planter un clou dans le mur, sous la plaque, qui va constituer un appui ponctuel ; on est alors isostatique.

Si l'on utilise plusieurs vis, on est dans le cas d'un hyperstatisme. En particulier, si le mur n'est pas strictement plan, la plaque va se déformer. Par contre, la fixation sera plus solide : le risque de dégradation accidentelle ou volontaire est réduit.

fixation hypostatique (vis seule)

fixation isostatique (vis + clou)

fixation hyperstatique (plusieurs vis)

On peut gérer cet hyperstatisme pour éviter la déformation de la plaque et s'assurer qu'elle soit bien parallèle au mur :

1. On commence par mettre en place toutes les vis, sans les serrer complètement ; on doit encore pouvoir éloigner ou rapprocher la plaque du mur ;
2. On serre les vis modérément et en croix : on commence par serrer un peu une vis, ce qui rapproche la plaque du mur, puis on serre la vis opposée, on procède de même pour les autres vis ; la plaque est maintenue contre le mur mais les vis ne sont pas serrées à fond ;
3. Une fois la plaque bien accolée au mur, on serre fermement les vis en croix.

Cette procédure s'applique aussi au serrage d'une roue de voiture par exemple.

Pour résumer :

• chaque contact supprime un ou plusieurs degrés de liberté ;
• supprimer un degré de liberté en translation revient à fixer la position en x ou en y ou en z de la pièce ;
• supprimer un degré de liberté en rotation revient à fixer l'orientation de la pièce selon un axe donné, x ou y ou z ;
• si l'on supprime deux fois un degré, on contraint deux fois la position ou l'orientation, et dans le cas réel, les deux contraintes ne sont pas strictement identiques, on a donc soit :
  • une instabilité, la pièce peut prendre deux positions différentes (table bancale), un seul des contacts est réalisé ;
  • une déformation, pour que les deux contacts soient réalisés.

Gestion de l'hyperstatisme

Dans certains cas, on ne peut pas éviter l'hyperstatisme ; dans d'autre cas, on se place volontairement dans un cas hyperstatique, afin que le dispositif résiste mieux aux charges mécaniques. Il faut donc gérer cet hyperstatisme.

On peut avoir un système qui s'adapte de manière dynamique. Par exemple, le premier rôle du système de suspension d'une voiture est de s'assurer que les quatre roues sont en permanence en contact avec le sol.

Mais dans la plupart des cas, le système n'a pas besoin de s'adapter en permanence, il suffit donc de prévoir une marge de manœuvre à l'installation, et éventuellement à la maintenance, donc un système réglable. On utilise fréquemment :

• un système qui permet d'ajuster la longueur d'une pièce ou l'écartement entre deux pièces : vis-écrou, système à crémaillère et cliquet, liaison glissière bloquée par frottement (vis de pression) ou par obstacle (goupille, bille à ressort et trous) ;
• un système permettant d'ajuster l'orientation ou la position :
  • fixation par boulon, le perçage d'une des pièces étant plus grand, ce qui permet de la déplacer ; on peut devoir utiliser une rondelle si la tête de vis ou l'écrou n'est pas assez grand,
  • fixation par boulon, le perçage d'une des pièce étant un trou oblong (lumière) ;
  • clouage, ou bien perçage des deux pièces au moment de l'installation puis fixation par boulon ou goupille ; contrairement aux solutions précédentes, cette solution n'est pas ajustable.

Sinon, il faut usiner les pièces avec une grande précision afin d'avoir des dimension très précises qui ne créent pas de contrainte excessive.

Point de vue mathématiques

Étude statique

Les actions mécaniques qui s'exercent sur les pièces peuvent se décrire par des forces et des moments, ou bien par des torseurs ; chaque action mécanique peut se décrire par six paramètres, en ayant choisi un repère dans l'espace :

• soit les trois composantes du vecteur force et les trois composantes du vecteur moment ;
• soit les six composantes du torseur d'action (X, Y, Z, L, M, N).

Si une pièce est immobile, le principe fondamental de la statique (PFS) fournit six équations, ce qui permet de calculer six inconnues. Si l'on a un assemblage de p pièces sans mobilité, on a donc 6×(p - 1) équations (la bâti est la pièce de référence, on ne s'intéresse pas à son immobilité), ce qui permet de lever 6×(p - 1) inconnues statiques. C'est le cas des structures.

Dans le cas d'un mécanisme, celui-ci réalise un certain nombre de mouvements. De fait, certaines équations de la statique ne s'appliquent plus. Lors de la phase initiale de la conception d'un mécanisme, on prévoit un certain nombre m_u de mouvements, dits « utiles » ; on a donc 6×(p - 1) - m_u équations, permettant de lever 6×(p - 1) - m_u inconnues statiques.

On peut laisser la possibilité à certaines pièces d'avoir des mouvements qui ne sont pas utiles au fonctionnement du mécanisme mais ne nuisent pas non plus à ce fonctionnement. Ces mobilités dites « inutiles », au nombre de m_i, permettent au mécanisme de s'adapter aux imprécisions de fabrication. On a donc 6×(p - 1) - m_u - m_i équations, permettant de lever 6×(p - 1) - m_u - m_i inconnues statiques.

La structure ou le mécanisme est soumis à des charges extérieures, qui sont normalement connues : elles font partie du fonctionnement normal du dispositif et ont été prévues dès le départ (avec un coefficient de sécurité). Mais cela génère des efforts sur les pièces qu'il faut calculer, afin de dimensionner les pièces, de choisir le matériau (calculs de résistance des matériaux). Les contacts entre les pièces sont modélisés par des liaisons ; les actions au niveau des liaisons sont les inconnues statiques qu'il faut déterminer, on en a au plus 6 par liaisons, et si l'on excepte la liaison encastrement, on a entre 1 et 5 inconnues statiques par liaison. Si l'on appelle N_s le nombre d'inconnues de liaisons, alors :

• si N_s = 6×(p - 1) - m_u - m_i, il y a autant d'équations que d'inconnues, on peut donc déterminer tous les efforts, c'est l'isostatisme ;
• si N_s < 6×(p - 1) - m_u - m_i, on a plus d'équations que d'inconnues, ce qui signifie les efforts ne sont pas définis en statique, donc qu'il y a des mouvements possibles qui nuisent à ce qui a été « planifié », à la fonctionnalité du système ; c'est l'hypostatisme ;
• si N_s > 6×(p - 1) - m_u - m_i, on a plus d'inconnues que d'équations, il est impossible de calculer tous les efforts avec la statique ; c'est l'hyperstatisme ^[3].

On définit alors le degré d'hyperstaticité h par :

h = N_s - (6×(p - 1) - m_u - m_i)

et l'on a :

• h < 0 : hypostatisme ;
• h = 0 : isostatisme ;
• h > 0 : hyperstatisme.

Lorsque l'on peut se ramener à un problème plan — c'est-à-dire lorsque les surfaces de contact et les actions transmissibles présentent une symétrie par rapport à un plan —, on n'a que trois inconnues statiques par action mécanique : les deux composantes du vecteur force dans le plan et le moment (qui est toujours perpendiculaire au plan), ou bien avec les torseurs les composantes X, Y et N (si l'on est dans le plan xy). Il ne reste donc plus que trois équations de statique par pièce, on peut donc déterminer 3×(p - 1) inconnues ; d'un autre côté, il y a aussi moins d'inconnues, puisque toutes les liaisons n'ont au plus que trois inconnues. En fait, toutes les liaisons peuvent se ramener aux liaisons encastrement (3 inconnues statiques), pivot dans le plan (d'axe normal au plan, 2 inconnues), glissière dans le plan (2 inconnues) ou appui ponctuel (1 inconnue). On a alors :

h = N_s - (3×(p - 1) - m_u - m_i).

Étude cinématique

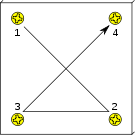
Lorsque l'on réalise le graphe des liaisons d'un système, on distingue des chaînes fermées : on part d'une pièce, on passe de pièce en pièce entre les pièces en contact, et on finit par revenir à la pièce de départ. On s'intéresse aux chaînes fermées indépendantes, c'est-à-dire que l'on ne peut pas décomposer en sous-chaînes. Le nombre de chaînes indépendantes, noté µ, est appelé nombre cyclomatique.

Si l'on a N_P pièces et N_L liaisons entre les pièces, on a alors un graphe de N_P sommets et N_L arcs. Le nombre cyclomatique vaut :

µ = N_L - N_P + 1.

Considérons une chaîne et numérotons ses pièces 1, 2, 3, …, n.

Bien évidemment, une pièce a un mouvement nul par rapport à elle-même. Si l'on appelle 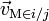la vitesse linéaire d'un par rapport à la pièce j et 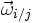la vitesse de rotation de i par rapport à j, alors la loi de composition des vitesses (relativité galiléenne) nous donne donc que :

ou bien avec les torseurs cinématiques :

.

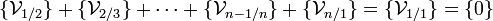Chaque vecteur ayant trois composantes, ou bien chaque torseur ayant six composantes, on a donc 6 équations par chaîne fermée. Le nombre d'équations total E vaut donc :

E = 6⋅µ.

Pour une liaison donnée entre une pièce i et une pièce j, le degré de liberté est le nombre d'inconnues cinématique entre i et j, le nombre de composantes non nulles dans 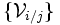. Si l'on somme les degrés de liberté d'un mécanisme, cela nous donne le nombre d'inconnues cinématiques I_C. On définit le degré de mobilité comme étant la différence I_C - E. Mais ce qui nous intéresse, c'est le nombre d'inconnues indépendantes. Dans les systèmes d'équation que donne la chaîne fermé, on peut déterminer le nombre d'équations indépendantes, appelé aussi rang du système d'équations Rg(E) ; on définit donc la mobilité m :

m = I_C - Rg(E).

Si m = 0, alors il n'y a pas d'inconnue cinématique, le système est immobile, figé. Le système a m mouvement indépendants.

On distingue

• les mobilités utiles m_u : les mouvements indépendants faisant intervenir un paramètre d'entrée ou de sortie du système (mouvement des pièces en contact avec l'extérieur du mécanisme) ;
• les mobilités internes, m_i : les mouvements indépendants ne faisant intervenir aucun paramètre d'entrée ou de sortie du système.

On a évidemment

m = m_u + m_i.

Le degré d'hyperstaticité h est défini par :

h = E - Rg(E)

et l'on a :

m - h = I_C - E

la mobilité est la différence entre le degré de mobilité et le degré d'hyperstaticité.

Détermination de l'isostatisme

Un solide est isostatique si et seulement si le nombre de liaisons indépendantes qui le lie à la fondation est égale au nombre de degrés de liberté de ce solide considéré sans ses points d'appuis. Cet état s'oppose aux états hyperstatique où leur nombre est plus élevé et hypostatique où le solide possède au moins un degré de liberté.

La position d'une pièce est donc donnée par 6 valeurs : les trois coordonnées (x, y, z) d'un de ses points (en général le centre d'inertie), et les trois angles définissant son orientation. On a donc six inconnues. Chaque liaison impose des équations. Il « suffit » donc de compter le nombre d'équations indépendantes fournies par les liaisons, et de le comparer au nombre d'inconnues (6 inconnues par pièce).

Dans le cas d'un système plan, on n'a que trois inconnues par pièce : les coordonnées (x, y) et l'angle de rotation dans le plan.

Positionnement isostatique d'une pièce à usiner

Lorsque l'on usine une pièce, le résultat doit être conforme au plan (dessin technique), et en particulier les tolérances géométriques. Le placement de la pièce doit être précis sur le chariot de la machine outil, la pièce doit donc être maintenue de manière isostatique. Dans la pratique, le maintien de la pièce est souvent hyperstatique, notamment pour que la pièce ne bouge pas sous les efforts engendrés par l'usinage, il faut donc gérer cet hyperstatisme.

Cas des structures métalliques

On se place dans le cas d'un problème plan, donc à trois inconnues par pièce.

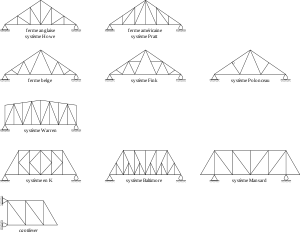
Une structure métallique (treillis, échafaudage, charpente, …) est composée de poutres — le terme « poutre » est à prendre au sens large : barre, tube, profilé, …—, et l'on considère qu'elles sont reliées entre elles par des pivots^[4]. On appelle « nœud » l'endroit où des poutres sont liées.

On utilise trois types de liaisons avec le sol ou le mur :

• appui simple ;
• articulation fixe (pivot) ;
• encastrement.

On peut dénombrer les inconnues de liaison qui sont levées par chacune des liaisons (cf. tableau ci-dessous) :

• l'appui simple empêche la translation perpendiculairement au plan d'appui, on fixe donc une inconnue ;
• l'articulation empêche les deux translations, on fixe donc deux inconnues ;
• l'encastrement immobilise tout, on fixe donc les trois inconnues.

Problème plan

Liaison	Inconnues de liaison fixées
appui simple	1
articulation	2
encastrement	3

La mobilité m est définie par^[5] :

m = nombre de poutre × 3 - nombre d'inconnues de liaison fixées.

On a :

• m > 0 : la structure est hypostatique (mobile, instable) ;
• m = 0 : la structure est isostatique ;
• m < 0 : la structure est hyperstatique.

Par rapport à l'étude statique, le nombre d'inconnues de liaison fixée est le nombre d'inconnues statiques N_s, et le nombre de poutres est p - 1 (le bâti étant le sol). On retrouve donc la formule du degré d'hyperstaticité dans le cas plan, le paramètre -m étant le degré d'hyperstaticité :

h = -m.

Lorsque l'on n'a que deux appuis, on peut utiliser une formule simplifiée. Si l'on appelle b le nombre de poutres et n le nombre de nœuds, on a^[6] :

• pour une structure sur appuis mobiles :
  m = 2×n - 3 - b ;
• pour une structure sur deux appuis fixes :
  m = 2×n - 4 - b.

Cas des mécanismes

Un mécanisme a pour but de générer un mouvement — actionneurs (vérins, moteurs) —, de transmettre ou de transformer un mouvement (bielle, engrenage, …). Un mécanisme est typiquement composé de plusieurs pièces. On considère ici que toutes les liaisons sont parfaites.

On peut donc définir

• la mobilité utile m_u : ce sont les mouvements possibles du mécanisme vis à vis de l'extérieur ; c'est le nombre de paramètres de position (coordonnées et angles de rotation) qu'il faut connaître pour définir la position des pièces d'entrée et de sortie du mécanisme (pièces en contact avec les solides extérieurs) ;
• la mobilité interne m_i : pour les pièces du mécanisme, ce sont les mobilités qui ne sont pas utiles au fonctionnement, mais qui ne sont pas gênantes ; c'est le nombre de paramètres de position (coordonnées et angles de rotation) qu'il faut connaître pour définir la position des pièces à l'intérieur du mécanisme.

On définit ainsi la mobilité du mécanisme :

m = m_u + m_i

Ces mobilités sont des nombres représentant le nombre de degrés de liberté. Ils sont obtenus en regardant les mouvements possibles ; il s'agit là d'une analyse qualitative.

Par ailleurs, chaque liaison entre pièces se caractérise par un torseur d'action. Certaines composantes de ce torseur sont forcées à zéro, les autres sont les inconnues statiques. On appelle N_s le nombre total d'inconnues statiques du mécanisme ; il est égale au nombre de degrés de liaisons de la liaisons, et c'est le complément à 6 du nombre de degrés de liberté. Si p est le nombre de pièces du mécanisme, bâti compris, on définit alors le degré d'hyperstastisme h par^[7] :

h = N_s + m - 6⋅(p - 1) = N_s + m_u + m_i - 6⋅(p - 1).

Si l'on a :

• h < 0 : le mécanisme a trop de mobilités et ne peut pas remplir sa fonction ;
• h = 0 : le mécanisme est isostatique, on peut tout calculer par la statique ;
• h > 0 : le mécanisme est hyperstatique, la statique ne suffit pas à calculer les inconnues statiques, c'est-à-dire les efforts auxquels seront soumises les pièces.

Dans le cas d'un système hyperstatique, les équations de la résistance des matériaux, et en particulier de la déformée des pièces, peut fournir des équations supplémentaires permettant de calculer les inconnues statiques. Sinon, il faut utiliser des spécifications géométriques très précises — et donc avec un surcoût — pour s'assurer que les inconnues hyperstatiques sont nulles.

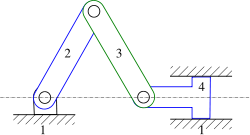
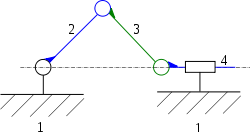
Exemple du système manivelle-bielle-piston

Considérons le système manivelle-bielle-piston. Ce système a une mobilités utiles : il suffit de connaître la position de la manivelle pour connaître la position du piston. On a donc

m_u = 1.

Ce mécanisme comporte quatre pièces (en comptant le bâti), donc

p = 4.

Les pièces doivent pouvoir pivoter entre elles dans le plan du mécanisme ; supposons que toutes les articulations internes soient des pivots. On a donc quatre liaisons cinématiques :

• trois pivots (n_s = 5), entre le bâti et la manivelle, la manivelle et la bielle et entre la bielle et le piston ;
• un pivot glissant (n_s = 4), entre le piston et le bâti,

soit

N_s = 3×5 + 4 = 19.

Par ailleurs, il n'y a pas de mobilité interne (les pivots sont fonctionnels donc pas « inutiles »), soit

m_i = 0 donc m = 1.

Le degré d'hyperstaticité vaut donc

h = 19 + 1 - 6×(4 - 1) = 2.

Le système est hyperstatique de degré 2. En effet, les deux pivots aux extrémités de la bielle lui imposent tousd les deux :

• sa position : l'axe de rotation de la manivelle peut être décalé par rapport à l'axe propre du piston ;
• son orientation autour de son axe : les axes aux extrémités de la bielle peuvent ne pas être coplanaires ;

il faudrait donc un parallélisme et un alignement parfaits des axes des pivots pour que l'inconnue hyperstatique soit nulle. Un mécanisme de ce type engendrerait des contraintes dans les pièces (risque de rupture), un frottement important (perte de rendement) et une usure prématurée des pièces.

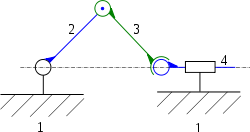
Une solution consiste par exemple à libérer la translation à une des extrémités de la bielle avec un pivot glissant et la rotation à l'autre avec une rotule — une faible amplitude de mouvement suffit. Les quatre liaisons cinématiques sont alors :

• un pivot (n_s = 5), entre le bâti et la manivelle ;
• une rotule (n_s = 3) entre la bielle et le piston ;
• deux pivots glissants (n_s = 4), entre la manivelle et la bielle et entre le piston et le bâti,

soit

N_s = 5 + 3 + 2×4 = 16,

et une mobilité inutile (la rotation du piston autour de son axe) :

m_i = 1 donc m = 2.

Le degré d'hyperstaticité vaut donc

h = 16 + 2 - 6×(4 - 1) = 0.

On a bien un système isostatique.

en:Linkage (mechanical)#Theory à traduire

Calcul des structures élastiques hyperstatiques

Une structure est dite hyperstatique si et seulement si le nombre de liaisons indépendantes qui la lie est supérieure au nombre de ses degrés de liberté.

Le degré d'hyperstaticité d'une structure est le nombres de liaisons à supprimer pour obtenir une structure isostatique.

Le calcul des structures élastiques hyperstatiques se réalise classiquement en considérant la poutre avec une coupure qui en limite le nombre de liaison et rend la poutre isostatique. Cette structure imaginaire provoque des réactions d'appuis que l'on peut calculer avec les équations d'équilibre statique. On trouve aussi les contraintes et les déformations au sein de cette structure imaginaire.

La structure réelle n'est pas cette structure imaginaire : des liaisons supplémentaires en lient les éléments. On calcule alors les efforts d'appuis nécessaires pour respecter les liaisons. Ce redressement se fait au prix d'un certain effort dans la poutre et de déformations que l'on peut calculer.

En vertus du principe de superposition, ces contraintes et ces déformations doivent être additionnées à celle de la structure hyperstatique imaginaire, et l'on trouve les contraintes et déformation de la structure réelle.

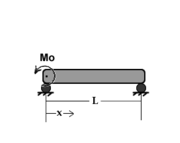
Poutre encastrée-appuyée sollicitée en son centre

Attention l'illustration utilisé n'est pas celui d'une poutre hyperstatique ! Les deux appuis doivent encastrés suivant l'axe longitudinal de la poutre.

Dans le cas d'une poutre encastrée-appuyée sollicitée en son centre d'un effort P (fig. 1), nous calculons tout d'abord une poutre bi-appuyée (fig.2).

Nous trouvons les réactions d'appuis égales chacune à la moitié de l'effort P et une déformée angulaire en O et l'angle de rotation en O,

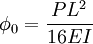
Reste à calculer le moment d'encastrement au point A. Ce moment est l'effort nécessaire pour atteindre un angle de déformée nulle en A, c'est à dire le moment provoquant une déformation exactement opposée à celle provoquée par la charge sur une poutre bi-appuyé que nous venons de calculer. Si nous en croyons les formules classiques, ce moment vaut

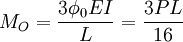
Ainsi, nous avons calculé toutes les réactions d'appuis et pouvons calculer les efforts et les déformations résultantes dans la poutre comme somme des effort dans la poutre isostatique et celui du à la réaction d'appuis supplémentaire que nous avons introduite.

Autre contexte d'utilisation

Gestion de production

L'isostatisme a pour objectif de déterminer la position relative de deux objets pour une phase de productique (transformation, manutention, mesure ou contrôle) en respectant la cotation de fabrication.

Lors d'une étude de mouvement avec un logiciel de conception (COSMOSMotion par exemple)

Lors de l'utilisation d'un simulateur de mouvement, par exemple COSMOSMotion (simulateur de mouvement intégré directement dans le logiciel Solidworks), il est important de connaître le degré d'hyperstatisme de l'assemblage avant d'utiliser le logiciel pour faire l'analyse de mouvement des pièces de l'assemblage (calcul des forces, moments ou vitesses). Il est impossible pour le logiciel de faire l'analyse si le système est hyperstatique, le logiciel désactivera donc par lui même certaines contraintes de l'assemblage et parfois celles-ci sont essentielles au bon fonctionnement du mécanisme. Cela peut engendrer des résultats erronés. Il faut donc s'assurer d'avoir un mécanisme isostatique avant de faire une analyse de mouvement avec un logiciel de CAO, ou du moins, s'assurer que celui-ci désactive les bonnes contraintes. Un bon moyen pour y arriver est de changer certains types de liaisons du mécanisme mais seulement pour l'étude, c'est-à-dire, faire une modification (qui peut être loufoque) seulement pour la modélisation sur le logiciel. Une fois l'étude accomplit, on peut remettre le mécanisme hyperstatique.

Voir aussi

• Théorie des mécanismes

Articles connexes

• Isostasie
• Productique
• Mécanique
• Technologie

Liens externes

• La symbolique MIP MAP
• Théorie des mécanismes, JDoTec

Bibliographie

Notes et références