- Isosurface
-
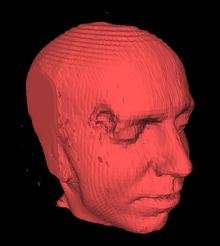Application du marching cubes pour représenter l'isosurface formée par les différents matériaux composants le crâne et la matière cérébrale
On peut considérer une isosurface comme l'analogue en 3D d'une courbe de niveau. C'est en fait le lieu des points de l'espace pour lesquels une certaine fonction (par exemple la pression, la température, la vitesse, la densité, etc.) est constante. En d'autres termes, c'est la courbe de niveau d'une fonction continue dont le domaine est l'espace ambiant.
En écriture mathématique, une isosurface est l'ensemble suivant : si la fonction f est celle dont on souhaite représenter l'isosurface en la valeur c, celle-ci est définie par :
On représente usuellement les isosurfaces à l'aide d'images de synthèse ; elles sont très utilisées comme méthode de représentation visuelle des données, notamment en Computational fluid dynamics (CFD), permettant ainsi aux ingénieurs d'étudier plus facilement les différents phénomènes intervenants en dynamique des fluides (pour les gaz et les fluides) autour d'objets, tels que les ailes d'avion. Une isosurface peut représenter une onde de choc particulière se produisant sur les vols supersoniques, ou plusieurs isosurfaces peuvent être générées pour étudier une séquence de valeurs de pressions dans l'air entourant une aile. Les isosurfaces tendent à devenir des moyens de visualisation privilégiés pour représenter efficacement des données volumiques, car elles peuvent être construites à l'aide de modèles polygonaux, qui sont affichés à l'écran très rapidement.
En imagerie médicale, les isosurfaces sont utilisées peut représenter des régions de densité donnée sur des Tomodensitométrie tridimensionnelle, permettant donc de visualiser de manière réaliste les organes internes, les os, ou d'autres structures corporelles.
De nombreux autres domaines sont intéressés par la représentation tridimensionnelle de données procurée par les isosurfaces pour en extraire aisément l'information, notamment la pharmacologie, chimie, géophysique et météorologie.
Une méthode très répandue de construction des isosurfaces repose sur l'algorithme du marching cubes.
Un exemple d'isosurface est la 'Metaball' utilisée intensivement en visualisation 3D.
Wikimedia Foundation. 2010.
