- Inégalité de Young
-
En mathématiques, la forme standard de l'inégalité de Young (ou inégalité d'Young) affirme que pour tous a et b réels posififs ou nuls et tous p et q réels strictement positifs tels que 1/p + 1/q = 1 (on dit parfois qu'ils sont conjugués), on a :
L'égalité a lieu si et seulement si ap = bq. L'inégalité de Young est un cas particulier de l'inégalité arithmético-géométrique. Son nom vient de William Henry Young.
Un cas simple (relativement fréquent) de l'inégalité de Young est l'inégalité avec des exposants 2 :
qui donne également l'inégalité de Young avec ε (valide pour tout ε > 0) :
Sommaire
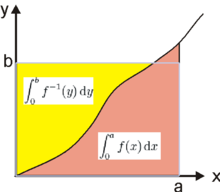
Généralisation utilisant des intégrales
Si f est une fonction croissante de [0,c] vers [0,f(c)], alors, pour tout
 et tout
et tout  , on a
, on a(où f − 1 est la bijection réciproque de f).
Le diagramme ci-contre donne une preuve graphique très simple de ce résultat, en interprétant les deux intégrales comme deux aires bordées par le graphe de f.
Le calcul précédent revient à dire que si f est une fonction convexe, en notant g sa transformée de Legendre[1], alors
 . Sous cette forme, cette inégalité est encore valide si f est une fonction convexe à argument vectoriel (voir Arnold, 1989, §14 en fin d'article).
. Sous cette forme, cette inégalité est encore valide si f est une fonction convexe à argument vectoriel (voir Arnold, 1989, §14 en fin d'article).Exemples
- La transformée de Legendre de f(a) = ap/p est g(b) = bq/q avec q tel que 1/p + 1/q = 1, et ainsi l'inégalité de Young standard est un cas particulier.
- La transformée de Legendre de f(a) = ea – 1 est g(b) = 1 – b + b ln b, et alors ab ≤ ea – b + b ln b pour tous a et b positifs ou nuls.
Une inégalité pour les normes Lp
En analyse réelle, le résultat suivant, démontré pour la première fois par Young en 1912 est aussi appelé inégalité de Young :
Soient f dans Lp et g dans Lq et
avec 1 ≤ p,q,r ≤ ∞ et 1/p + 1/q ≥ 1. Alors
Où l'étoile note ici le produit de convolution, Lp est l'espace de Lebesgue et
note la norme Lp usuelle. Ceci peut être démontré par l'inégalité de Hölder.
Utilisation
L'inégalité de Young peut être utilisée dans la preuve de l'inégalité de Hölder. Elle est également largement utilisée pour estimer la norme de termes non linéaires en théorie des équations aux dérivées partielles, puisqu'elle permet d'estimer un produit de deux termes par une somme des deux mêmes termes à une puissance quelconque et divisé par un nombre.
Démonstrations
Cas élémentaire
L'inégalité de Young avec des exposants 2 est le cas particulier p = q = 2. Sinon, elle a une preuve élémentaire en observant seulement que
on ajoute 2ab de chaque côté et on divise par 2.
L'inégalité de Young avec ε suit en appliqant l'inégalité de Young avec exposants 2 à
Forme standard
La démonstration est triviale si a = 0 or b = 0. On suppose donc a, b > 0.
Si ap = bq, alors, en utilisant 1/p + 1/q = 1 :
et on a l'égalité dans l'inégalité de Young.
Supposons maintenant ap ≠ bq jusqu'à la fin de la preuve. Par l'équation fonctionnelle du logarithme naturel, on a :
En notant que le logarithme naturel est strictement croissant (parce que sa dérivée est strictement positive), alors ln ap ≠ ln bq. Sa fonction réciproque est la fonction exponentielle f(x) = exp(x), qui est une fonction strictement convexe (puisque sa dérivée seconde est strictement positive). Ainsi la fonction exponentielle satisfait la définition des fonctions strictement convexes : pour tous t de l'intervalle ouvert ]0,1[ et tous nombres réels x et y avec x ≠ y, on a :
 .
.
En appliquant l'inégalité stricte pour t = 1/p, 1 – t = 1/q, x = ln ap et y = ln bq, on obtient :
ce qui termine la preuve.
Notes
- c'est-à-dire que g est la primitive de la réciproque de la dérivée de f
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Young inequality » (voir la liste des auteurs)
- Vladimir Igorevitch Arnold, Mathematical Methods of Classical Mechanics, Springer, 1989, 2de éd. (ISBN 978-0-387-96890-2)
- William Henry Young, « On the multiplication of successions of Fourier constants », dans Proc. Roy. Soc. Lond. Series A, vol. 87, p. 331-339
Wikimedia Foundation. 2010.