Indices de Miller et indices de direction

Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction.

Un cristal est un empilement ordonné d'atomes, d'ions ou de molécules, appelés ci-après « motifs ». La périodicité du motif est exprimée par un réseau constitué de nœuds qui représentent les sommets de la maille. Les arêtes de la maille conventionnelle définissent les vecteurs de la base. Les plans et directions sont qualifiés de « nodaux » (plan nodal, direction nodale) ou mieux encore « réticulaires ». Une direction réticulaire est dite rangée.

En métallurgie, on travaille fréquemment avec des cristaux constitués d'un seul type d'atomes ; on parle donc de « plan atomique », de « direction atomique » ou de « rangée d'atomes », mais ce ne sont que des cas particuliers.

Sommaire

1 Importance des plans et directions denses
2 Repérage d'une direction
3 Repérage d'un plan
4 Symétries cristallines et permutation des indices
- 4.1 Cristal à symétrie cubique
- 4.2 Cristal à symétrie hexagonale
5 Calculs géométriques dans l'espace réciproque
- 5.1 Distance interréticulaire
- 5.2 Angle entre plans réticulaires
6 Indexation des pics de diffraction
7 Espace réciproque et diffraction
8 Notes
9 Voir aussi
- 9.1 Articles connexes
- 9.2 Liens externes

Importance des plans et directions denses

Plan cristallographique et densité atomique.
Bas : cristal de profil.
Haut : vues selon un axe perpendiculaire à chaque surface.

Le cristal n'est pas isotrope^[1], il n'y a pas de raison que ses propriétés le soient. Les lignes et plans de grande densité vont présenter des propriétés particulières :

optiques : la propagation d'une onde lumineuse dans le cristal (réfraction) se fait par diffusion Rayleigh de proche en proche, entre les atomes ; la vitesse de propagation peut donc différer selon la densité de la direction, provoquant le phénomène de biréfringence ;
liées à la tension superficielle : si le matériau se condense sous la forme d'un cristal, c'est qu'un motif est plus stable lorsqu'il est entouré d'autres motifs ;
- propagation d'une fissure et plan de clivage : les motifs d'une surface libre sont exposés à l'air ; la surface libre est plus stable si elle correspond à un plan de grande densité, car alors chaque motif est entouré d'un maximum de motifs ;
- forme d'un pore, pour la même raison que ci-dessus ;
adsorption et réactivité : le nombre de sites d'adsorption, et donc la réactivité chimique, dépend de la densité d'atomes ;
dislocations :
- le cœur d'une dislocation va plus s'étendre dans un plan dense, cela réduit le frottement lors du déplacement de la dislocation (force de Peierls-Nabarro au cours de la déformation plastique) ; les glissements se font donc préférentiellement selon des plans denses ;
- la perturbation que représente une dislocation (vecteur de Burgers) est une direction dense : en effet, un décalage d'un motif dans une direction dense représente une distorsion faible (les motifs étant rapprochés) ;
- la ligne d'une dislocation va également tendre à être une direction dense, afin de diminuer la tension de ligne (une boucle de dislocation aura donc tendance à être un polygone).

Repérage d'une direction

Exemples de directions.

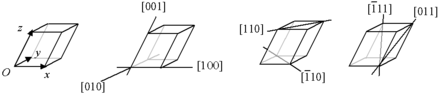
Une direction peut se représenter par un vecteur. On choisit pour cela un vecteur ayant des coordonnées entières : une direction contient au moins deux motifs pour que l'on puisse définir sa densité ; les motifs sont décalés d'une combinaison linéaire entière des vecteurs de la base. Cette direction est notée $[uvw]$ où $u$ , $v$ et $w$ sont les coordonnées entières. Les nombres négatifs sont notés avec un trait au-dessus ( $u$ se lit « moins $u$ ») :

[111] (ou le vecteur opposé [111]) désigne la grande diagonale de la maille ;
[111] (ou l'opposé [111]) et [111] (ou l'opposé [111]) désignent les deux autres diagonales ;
[100], [010] et [001] désignent les vecteurs de la base.

Si l'on note $\vec{a}$ , $\vec{b}$ et $\vec{c}$ les vecteurs de la base, alors les indices de direction [uvw] correspondent au vecteur

$u\vec{a} + v\vec{b} + w\vec{c}$

$u$ , $v$ et $w$ sont des coordonnées de type contravariantes.

Note: Dans le cas général, la base $(\vec{a}, \vec{b}, \vec{c})$ est quelconque. C'est une base orthogonale dans le cas d'un réseau à symétrie orthorhombique ou tétragonale, et orthonormale dans le cas d'un réseau à symétrie cubique (voir l'article Réseau de Bravais).

Repérage d'un plan

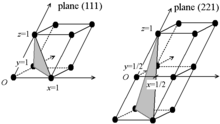
Définition des indices de Miller d'un plan.

Considérons le plan le plus proche de l'origine mais qui ne passe pas par l'origine. Si l'on prend l'intersection de ce plan avec les trois axes, on obtient les trois coordonnées de trois points :

$(P,0,0)$ l'intersection du plan avec l'axe des x ;
$(0, Q,0)$ l'intersection du plan avec l'axe des y ;
$(0,0, R)$ l'intersection du plan avec l'axe des z ;

alors l'inverse des coordonnées des intersections donne les indices de Miller, avec la convention 1/∞ = 0 (l'indice est 0 si l'axe est parallèle au plan). Ces indices sont notés entre parenthèses $(hkl)$ :

$h = 1/ P$ ;
$k = 1/ Q$ ;
$l = 1/ R$ .

Exemples de plans pour une structure cubique.

Si ni $h$ , ni $k$ , ni $l$ ne sont nuls, alors le plan passe donc par les points $A 1 (1/ h,0,0)$ , $A 2 (0,1/ k,0)$ , $A 3 (0,0,1/ l)$ , donc les vecteurs suivants sont dans le plan :

$\overrightarrow{A_1 A_2} \left ( -\frac{1}{h}, \frac{1}{k}, 0 \right )$ ;
$\overrightarrow{A_1 A_3} \left ( -\frac{1}{h}, 0, \frac{1}{l} \right )$ ;
$\overrightarrow{A_2 A_3} \left ( 0, -\frac{1}{k}, \frac{1}{l} \right )$ .

Ces vecteurs n'étant pas colinéaires, deux de ces vecteurs forment une base du plan.

Si un des indices est nul, alors un des vecteurs de la base de la maille est aussi un vecteur du plan, celui dont la composante non nulle est l'indice nul du plan :

si $h = 0$ , le vecteur [1 0 0] (vecteur de coordonnées (1,0,0)) est dans le plan ;
si $k = 0$ , le vecteur [0 1 0] est dans le plan ;
si $l = 0$ , le vecteur [0 0 1] est dans le plan.

Si la base est orthonormale, le produit scalaire du vecteur $[hkl]$ avec ces vecteurs est nul :

$\left ( -\frac{1}{h}, \frac{1}{k}, 0 \right ) \cdot (h,k,l) = -1 + 1 + 0 = 0$

$\left ( -\frac{1}{h}, 0, \frac{1}{l} \right ) \cdot (h,k,l) = -1 + 0 + 1 = 0$

$\left ( 0, -\frac{1}{k}, \frac{1}{l} \right ) \cdot (h,k,l) = 0 -1 + 1 = 0$

Donc dans le cas d'un réseau cubique, le vecteur $[hkl]$ est perpendiculaire à la surface, c'en est un vecteur normal. Dans le cas général, il faut changer de base pour que le vecteur de coordonnées $(h, k, l)$ soit perpendiculaire au plan (cf. infra).

Symétries cristallines et permutation des indices

Certaines structures cristallines possèdent des symétries particulières permettant la permutation des indices.

Cristal à symétrie cubique

Pour un cristal suivant un réseau de Bravais cubique, les trois diagonales sont équivalentes, les trois faces du cube sont équivalentes, … ; on peut donc permuter à volonté les indices et prendre les opposés d'un ou de plusieurs indices, cela représentera immuablement une direction ayant les mêmes propriétés.

L'ensemble des directions obtenues par permutation est appelé « famille de direction », qui est notée entre crochet :

< uvw >

désigne à la fois

[uvw]

[uwv]

[vuw]

[vwu]

[wuv]

[wvu]

ainsi que les combinaisons obtenues en changeant un ou deux signes.

Par exemple :

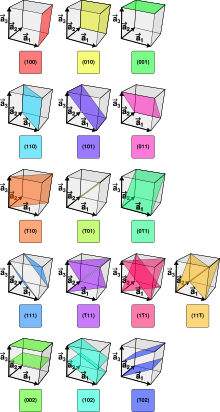
<100> désigne les directions [100], [100], [010], [010], [001] et [001] ;
<110> désigne les directions [110], [110], [110], [101], [101], [101], [011], [011] et [011] (ainsi que leurs directions opposées).

Il en est de même pour les plans, on peut permuter les indices de Miller. Une famille de plans équivalents par symétrie est alors notée entre accolades :

{hkl}

désigne les plans

(hkl)

(hlk)

(khl)

(klh)

(lhk)

(lkh)

ainsi que les combinaisons obtenues en changeant un ou deux signes.

Cristal à symétrie hexagonale

Indices de Miller-Bravais.

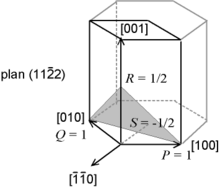
Dans le cas des structures à symétrie hexagonale, ou trigonale, on définit parfois un quatrième indice pour désigner les plans, $(hkil)$ ; c'est la notation de Bravais-Miller. L'indice $i$ , placé en troisième position, est redondant (les trois indices $h$ , $k$ et $l$ suffisent à eux seuls à définir un plan) ; il est défini par

i = - h - k

Cette notation permet d'appliquer des permutations circulaires d'indices pour définir des familles de plans.

En fait, si l'on considère le plan de base (001), ce plan a une symétrie d'ordre 3, c'est-à-dire qu'il est invariant par une rotation d'1/3 de tour (2π/3 rad, 120 °). Il contient donc trois directions identiques [100], [010] et [110]. Si l'on prend l'intersection du plan avec ces trois axes, l'inverse des abscisses des intersections donnent les indices $h$ , $k$ et $i$ .

Calculs géométriques dans l'espace réciproque

Distance interréticulaire

Article détaillé : Distance interréticulaire.

La distance interréticulaire d_hkl entre deux plan de la famille ${h k l}$ est donnée par :

$d_{hkl} = \frac{1}{\|\vec{H}\|} = \frac{1}{\sqrt{\vec{H}^{T} G^* \vec{H}}}$

où :

$\vec{H}=h\vec{a_r}+k\vec{b_r}+l\vec{c_r}$ est le vecteur normal à un plan de la famille {hkl) ;
$\vec{a^*}$ , $\vec{b^*}$ et $\vec{c^*}$ sont les vecteurs de base du réseau réciproque ;
$\vec{H}^T$ est la transposée du vecteur $\vec{H}$ ;
$G^*~$ est le tenseur métrique du réseau réciproque.

Angle entre plans réticulaires

L'angle $θ$ entre deux plans réticulaires $(h k l) 1$ et $(h k l) 2$ est l'angle entre leurs normales $\vec{H_1}$ et $\vec{H_2}$ . Il est donné par :

$\cos{\theta} = \frac{(\vec{H_1} | \vec{H_2})}{\|\vec{H_1}\| \|\vec{H_2}\|}$

avec

$(\vec{H_1} | \vec{H_2}) = \vec{H_1}^T G^* \vec{H_2}$
$\| \vec{H_i} \|= \sqrt{\vec{H_i}^T G^* \vec{H_i}}$

où :

$\vec{H_i} = h_i \vec{a^*} + k_i \vec{b^*} + l_i \vec{c^*}$ est un vecteur normal au plan $(h k l) i$ ;
$\vec{a^*}$ , $\vec{b^*}$ et $\vec{c^*}$ sont les vecteurs de base du réseau réciproque ;
$\vec{H_i}^T$ est la transposée du vecteur $\vec{H_i}$ ;
$G^*~$ est le tenseur métrique du réseau réciproque.

Indexation des pics de diffraction

Dans les expériences de diffraction avec une longueur d'onde de l'ordre des paramètres de maille (diffraction de rayons X, diffraction de neutrons, diffraction d'électrons en microscopie électronique en transmission), la position des pics^[2] de diffraction peut se calculer en fonction des distances interréticulaires, par la loi de Bragg.

On peut ainsi relier chaque pic à un plan $(hkl)$ ; les indices de miller du plan sont les indices du pic.

Espace réciproque et diffraction

Considérons l'espace réciproque, c'est-à-dire l'espace vectoriel formé par les vecteurs d'onde ; l'utilisation de cet espace permet de déterminer facilement les conditions de diffraction (voir aussi l'article Théorie de la diffraction sur un cristal).

On y définit la base réciproque $(\vec{e}^*_1, \vec{e}^*_2, \vec{e}^*_3)$ par^[3]

$\vec{e^*_1} = \frac{1}{V} \cdot \vec{e}_2 \wedge \vec{e}_3$

$\vec{e^*_2} = \frac{1}{V} \cdot \vec{e}_3 \wedge \vec{e}_1$

$\vec{e^*_3} = \frac{1}{V} \cdot \vec{e}_1 \wedge \vec{e}_2$

où V est le volume de la maille $(\vec{e_1},\vec{e_2},\vec{e_3})$ qui peut s'écrire :

$V = \vec{e_1} \cdot (\vec{e_2} \wedge \vec{e_3}) = \vec{e_3} \cdot (\vec{e_1} \wedge \vec{e_2}) = \vec{e_2} \cdot (\vec{e_3} \wedge \vec{e_1})$ .

D'après les propriétés du produit vectoriel, on a

$\vec{e_1^*} \cdot \vec{e_2} = \vec{e_1^*} \cdot \vec{e_3} = 0$ , soit $\vec{e_1^*} \bot \vec{e_2}$ et $\vec{e_1^*} \bot \vec{e_3}$

$\vec{e_2^*} \cdot \vec{e_3} = \vec{e_2^*} \cdot \vec{e_1} = 0$ , soit $\vec{e_2^*} \bot \vec{e_3}$ et $\vec{e_2^*} \bot \vec{e_1}$

$\vec{e_3^*} \cdot \vec{e_1} = \vec{e_3^*} \cdot \vec{e_2} = 0$ , soit $\vec{e_3^*} \bot \vec{e_1}$ et $\vec{e_3^*} \bot \vec{e_2}$

Par ailleurs, si (m, n, p) est une permutation circulaire de (1, 2, 3), on a^[4]

$\vec{e_m} \cdot \vec{e_m^*} = \frac{1}{V} \cdot (\vec{e_m}\cdot \vec{e_n} \wedge \vec{e_p}) = 1$ .

Notons $\vec{K}$ le vecteur ayant les coordonnées (h, k, l) dans cette base réciproque :

$\vec{K} = h \cdot \vec{e^*_1} + k \cdot \vec{e^*_2} + l \cdot \vec{e^*_3}$

alors ce vecteur est normal au plan (hkl) : si ni h, ni k, ni l ne sont nuls, alors

$\vec{K} \cdot \overrightarrow{A_1 A_2} = (h \cdot \vec{e^*_1} + k \cdot \vec{e^*_2} + l \cdot \vec{e^*_3}) \cdot \left ( -\frac{1}{h} \cdot \vec{e_1} + \frac{1}{k} \cdot \vec{e_2} \right )$

soit

$\vec{K} \cdot \overrightarrow{A_1 A_2} = -\vec{e^*_1} \cdot \vec{e_1} + \frac{h}{k} \cdot \vec{e^*_1} \cdot \vec{e_2} -\frac{k}{h} \cdot \vec{e^*_2} \cdot \vec{e_1} + \vec{e^*_2} \cdot \vec{e_2} - \frac{l}{h} \cdot \vec{e^*_3} \cdot \vec{e_1} + \frac{l}{k} \cdot \vec{e^*_3} \cdot \vec{e_2}$

donc

$\vec{K} \cdot \overrightarrow{A_1 A_2} = -1 + 0 - 0 + 1 - 0 + 0 = 0$ ^[5]

donc $\vec{K} \bot \overrightarrow{A_1 A_2}$ . On peut démontrer de même que $\vec{K} \bot \overrightarrow{A_2 A_3}$ et que $\vec{K} \bot \overrightarrow{A_3 A_1}$ . Le vecteur $\vec{K}$ est perpendiculaire à deux vecteurs non colinéaires du plan, il est donc normal au plan. Si h, k ou l est nul, on montre l'orthogonalité en se basant sur le fait qu'un ou deux des axes est parallèle au plan.

Or, les vecteurs ayant des coordonnées entières dans la base réciproque correspondent aux conditions de diffraction. Ainsi :

dans le cas de la diffraction sur un monocristal (cliché de Laue, microscopie électronique en transmission), on peut associer une tache de diffraction à un plan cristallographique ;
dans le cas d'une poudre (chambre de Debye-Scherrer, diffractomètre Bragg-Brentano), on peut associer un anneau de Debye ou un pic de diffraction à un plan cristallographique.

On parle ainsi de tache, d'anneau ou de pic (hkl). Cette association s'appelle « l'indexation ».

Notes

↑ Les cristaux cubiques sont toutefois appelés isotropes à cause de l'isotropie de leurs propriétés optiques.
↑ Par « pic », nous désignons non seulement les pics des diffractogrammes dans le cas des enregistrements numériques, mais aussi les taches de diffraction dans le cas de la diffraction sur un monocristal (cliché de Laue, microscopie électronique en transmission), ainsi que les anneaux de diffraction dans le cas de la diffraction sur une poudre (chambre de Debye-Scherrer). Voir l'article Théorie de la diffraction sur un cristal.
↑ Il existe deux manières de définir le vecteur d'onde ; soit sa norme est 1/λ, on a alors les formules indiquées ; soit sa norme est 2π/λ et on a alors $\vec{e^*_i} = \frac{2 \pi}{V} \cdot \vec{e_j} \wedge \vec{e_k}$ (i, j, k) étant une permutation circulaire de (1, 2, 3) ; ce facteur 2π produit juste une homothétie (dilatation) de l'espace réciproque, mais ne change rien aux résultats.
↑ Si l'on choisit de prendre 2π/λ pour la norme du vecteur d'onde, alors $\vec{e_m} \cdot \vec{e_m^*} = \frac{2 \pi}{V} \cdot (\vec{e_m}\cdot \vec{e_n} \wedge \vec{e_p}) = 2 \pi$ .
↑ Si l'on choisit de prendre 2π/λ pour la norme du vecteur d'onde, alors $\vec{K} \cdot \overrightarrow{A_1 A_2} = -2 \pi +0 -0 + 2 \pi -0 + 0 = 0$ .

Voir aussi

Liens externes

Sur les autres projets Wikimedia :

« Indices de Miller et indices de direction », sur Wikimedia Commons (ressources multimédia)

Éléments de cristallographie
- Plans nodaux et indices de Miller
- Indices de Miller

Catégorie :

Cristallographie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Indices de Miller et indices de direction de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Indices de direction — Indices de Miller et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un… … Wikipédia en Français
Indices De Miller — et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un empilement ordonné d … Wikipédia en Français
Indices de Miller — et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un empilement ordonné d … Wikipédia en Français
Indices de miller — et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un empilement ordonné d … Wikipédia en Français
Miller index — Planes with different Miller indices in cubic crystals … Wikipedia
Indice de Miller — Indices de Miller et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un… … Wikipédia en Français
Indice de direction — Indices de Miller et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un… … Wikipédia en Français
R. C. Miller — Robert C. Miller Pour les articles homonymes, voir Miller. Robert C. Miller Naissance 1920 Los … Wikipédia en Français
Robert C. Miller — Pour les articles homonymes, voir Miller. Robert C. Miller Naissance 1920 Los Angeles ( … Wikipédia en Français
Plan réticulaire — Indices de Miller et indices de direction Les indices de Miller sont une manière de désigner les plans dans un cristal. On utilise des indices similaires pour désigner les directions dans un cristal, les indices de direction. Un cristal est un… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Indices de Miller et indices de direction

Sommaire

Importance des plans et directions denses

Repérage d'une direction

Repérage d'un plan