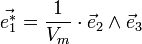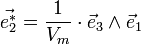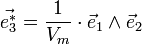Reseau reciproque

Reseau reciproque

Réseau réciproque

Un cristal peut se décrire comme un réseau aux nœuds duquel se trouvent des motifs : atome, ion, molécule.

Si l'on appelle 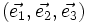(\vec{e_1}, \vec{e_2},\vec{e_3}) les vecteurs définissant la maille élémentaire, ces vecteurs définissent une base de l'espace. On peut définir une base réciproque par 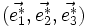(\vec{e^*_1}, \vec{e^*_2}, \vec{e^*_3}) vérifiant [1]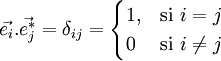

\vec{e_i}.\vec{e^*_j} = \delta_{ij} = \begin{cases} 1, & \text{si }i=j \\ 0 & \text{si }i\ne j \end{cases}

ce qui donne

\vec{e^*_1} = \frac{1}{V_m} \cdot \vec{e}_2 \wedge \vec{e}_3
\vec{e^*_2} = \frac{1}{V_m} \cdot \vec{e}_3 \wedge \vec{e}_1
\vec{e^*_3} = \frac{1}{V_m} \cdot \vec{e}_1 \wedge \vec{e}_2

où Vm est le volume de la maille du réseau direct :

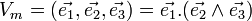
V_m = (\vec{e_1},\vec{e_2},\vec{e_3}) = \vec{e_1}.(\vec{e_2} \wedge \vec{e_3})


Les points ayant des coordonnées entières dans le repère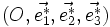 (O, \vec{e^*_1}, \vec{e^*_2},\vec{e^*_3}) forment un réseau appelé réseau réciproque.

Sommaire

Application

L'étude des cristaux se fait en général par diffraction d'un rayonnement ayant une longueur d'onde de l'ordre de la distance inter-atomique. À partir de la figure de diffraction obtenue, on peut déterminer la forme du réseau, et donc la structure du cristal.

Si l'on appelle

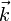  • \vec{k} le vecteur d'onde du rayonnement incident ;
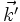  • \vec{k'} le vecteur des ondes diffusées dans une direction donnée ;
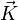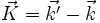  • \vec{K} le vecteur de diffusion (ou vecteur de diffraction) défini par \vec{K} = \vec{k'} - \vec{k} ;

alors la condition de diffraction sur un monocristal est donnée par le théorème de Bloch :

il y a diffraction si 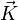\vec{K} est un vecteur du réseau réciproque.

Table des réseaux réciproques

Pour trouver le réseau réciproque il faut considérer la maille primitive. On utilise par contre couramment des réseaux non-primitifs, comme le cubique centré (2 nœuds par maille) et le cubique faces centrées (4 nœuds par maille).

Réseau (paramètre) : Réseau réciproque (paramètre) :
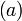
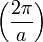
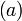
cubique \left(a\right) cubique \left(\frac{2\pi}{a}\right)
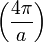
cubique centré \left(a\right) cubique faces centrées \left(\frac{4\pi}{a}\right)
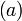
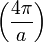
cubique faces centrées \left(a\right) cubique centré \left(\frac{4\pi}{a}\right)

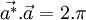
Ici on a posé \vec{a^*}.\vec{a}=2.\pi

Note

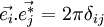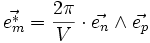  1. ↑ il existe deux manières de définir le vecteur d'onde ; soit sa norme est 1/λ, on a alors les formules indiquées ; soit sa norme est 2π/λ et on a alors \vec{e_i}.\vec{e^*_j} = 2\pi\delta_{ij} et \vec{e_m^*} = \frac{2 \pi}{V} \cdot \vec{e_n} \wedge \vec{e_p} où (m, n, p) est une permutation circulaire de (1, 2, 3)

Voir aussi

  • Portail de la chimie Portail de la chimie
  • Portail de la physique Portail de la physique
Ce document provient de « R%C3%A9seau r%C3%A9ciproque ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Reseau reciproque de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Réseau réciproque — En cristallographie, le réseau réciproque d un réseau de Bravais est l ensemble des vecteurs tels que pour tous les vecteurs position du réseau de Bravais. Ce réseau réciproque est lui même un réseau de Bravais, et son réseau réciproque est le… …   Wikipédia en Français

  • réseau réciproque — atvirkštinė gardelė statusas T sritis fizika atitikmenys: angl. dual lattice; reciprocal lattice vok. Dualgitter, n; reziprokes Gitter, n rus. обратная решётка, f pranc. réseau dual, m; réseau réciproque, m …   Fizikos terminų žodynas

  • vecteur de réseau réciproque — atvirkštinės gardelės vektorius statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorius, kurio skaliarinė sandauga iš kiekvieno pagrindinio gardelės vektoriaus lygi sveikajam skaičiui, padaugintam iš 2π. atitikmenys: angl. angular… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • vecteurs de base du réseau réciproque — pagrindiniai atvirkštinės gardelės vektoriai statusas T sritis Standartizacija ir metrologija apibrėžtis Pagrindiniai atvirkštinės gardelės transliacijos vektoriai. atitikmenys: angl. fundamental reciprocal lattice vectors pranc. vecteurs de base …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • vecteur de réseau réciproque — atvirkštinės gardelės vektorius statusas T sritis fizika atitikmenys: angl. inverse lattice vector; reciprocal lattice vector vok. inverse Gittervektor, m; Vektor des reziproken Gitters, m rus. вектор обратной решётки, m pranc. vecteur de réseau… …   Fizikos terminų žodynas

  • réseau — [ rezo ] n. m. • XIIIe; resel « filet » XIIe; de rets ou, par substit. de suff., de reseuil (vx), lat. retiolus, dimin. de retis → rets 1 ♦ Vx Tissu à mailles très larges; filet. ⇒aussi lacis …   Encyclopédie Universelle

  • réseau dual — atvirkštinė gardelė statusas T sritis fizika atitikmenys: angl. dual lattice; reciprocal lattice vok. Dualgitter, n; reziprokes Gitter, n rus. обратная решётка, f pranc. réseau dual, m; réseau réciproque, m …   Fizikos terminų žodynas

  • Réseau (groupe) — Réseau (géométrie) Pour les articles homonymes, voir Réseau. Un réseau est un ensemble discret de points qui emplissent un e …   Wikipédia en Français

  • Reseau d'echanges reciproques de savoirs — Réseau d échanges réciproques de savoirs Un Réseau d Échanges Réciproques de Savoirs ( RERS ), est une association fonctionnant à l échelle d une agglomération, une zone rurale ou d une entreprise et dont les membres donnent et reçoivent des… …   Wikipédia en Français

  • Réseau d'Echanges Réciproques de Savoirs — Réseau d échanges réciproques de savoirs Un Réseau d Échanges Réciproques de Savoirs ( RERS ), est une association fonctionnant à l échelle d une agglomération, une zone rurale ou d une entreprise et dont les membres donnent et reçoivent des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”