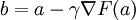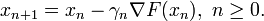- Algorithme de descente
-
Descente de gradient
La descente de gradient désigne un algorithme d'optimisation. Afin de trouver un minimum local de la fonction à optimiser, cette méthode consiste à progresser par étapes proportionnelles à l'opposé du gradient (ou de son approximation) de la fonction au point courant. À l'opposé, en progressant par étapes dans la direction du gradient, on obtient alors un maximum local de la fonction ; cette méthode est alors appelée montée de gradient (gradient ascent en anglais).La descente de gradient est également connue sous les noms de descente de plus forte pente ou méthode de la plus grand pente car l'antigradient définit la meilleure des directions de descente. Quand elle est connue sous ces dernières appellations, cette méthode ne doit pas être confondue avec la méthode de plus grande pente utilisée pour l'approximation d'intégrales.
Sommaire
Algorithme
La descente de gradient est basée sur l'observation que si une fonction
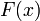 à valeurs dans
à valeurs dans  est définie et différentiable (dérivable pour une fonction définie sur
est définie et différentiable (dérivable pour une fonction définie sur  ) en un point
) en un point 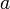 , alors
, alors 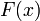 décroît le plus rapidement dans une direction opposée à celle du gradient de F en
décroît le plus rapidement dans une direction opposée à celle du gradient de F en 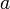 ,
, 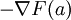 . Ainsi, si l'on définit
. Ainsi, si l'on définit 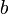 comme suit :
comme suit :pour γ > 0 suffisamment petit, alors on a
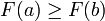 . Ainsi, en conservant cette observation en tête, on peut initialiser l'algorithme à une valeur x0, première approximation de la position du minimum local de F, et calculer la séquence
. Ainsi, en conservant cette observation en tête, on peut initialiser l'algorithme à une valeur x0, première approximation de la position du minimum local de F, et calculer la séquence 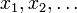 telle que :
telle que :On a alors
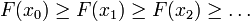 ,
,
et ainsi la série (xn) converge vers le minimum local désiré. Également, le pas γ peut varier à chaque itération.
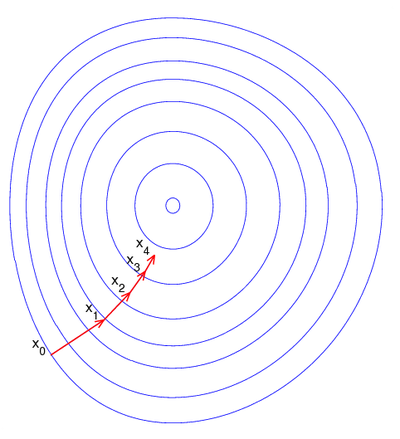 Descente de gradient sur une fonction de type bol (vue en plan avec lignes de niveaux).
Descente de gradient sur une fonction de type bol (vue en plan avec lignes de niveaux).
L'évolution des points xn au cours de la méthode est illustrée sur la figure de droite. Dans cette figure, on suppose que F est définie sur le plan (
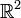 ), et qu'elle représente une forme de bol. Les courbes bleues correspondent aux lignes de niveaux, c'est à dire les lignes sur lesquelles F est constante. Les vecteurs rouges montrent la direction de l'opposé du gradient à leur point d'origine. Il est intéressant de noter également que le gradient (et son opposé) en un point donné est orthogonal à la ligne de niveau en ce point. On peut donc obesrver ici comment la descente de gradient progresse vers le fond du bol, c'est à dire vers le point où la valeur de F est minimale.
), et qu'elle représente une forme de bol. Les courbes bleues correspondent aux lignes de niveaux, c'est à dire les lignes sur lesquelles F est constante. Les vecteurs rouges montrent la direction de l'opposé du gradient à leur point d'origine. Il est intéressant de noter également que le gradient (et son opposé) en un point donné est orthogonal à la ligne de niveau en ce point. On peut donc obesrver ici comment la descente de gradient progresse vers le fond du bol, c'est à dire vers le point où la valeur de F est minimale.Exemples et limitations
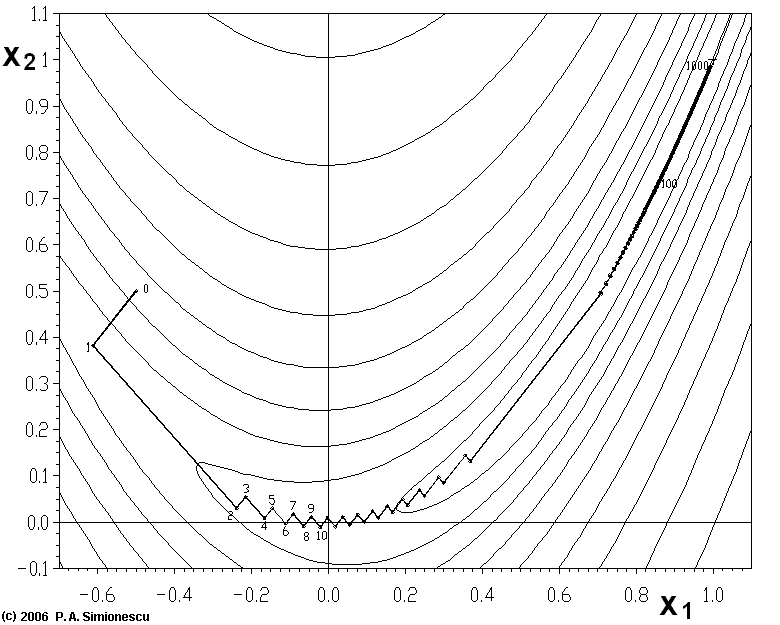
L'algorithme de descente de gradient peut rencontrer un certain nombre de problèmes avec des fonctions pathologiques comme par exemple la fonction de Rosenbrock illustrée ici. Cette fonction contient en effet une vallée très resserrée et courbée qui inclut le minimum. Le fond de la vallée est également très plat. A cause de cette vallée courbe et presque plane, l'optimisation zigzague au fond de la vallée vers le minimum en utilisant de très petits pas et se révèle donc très lente.
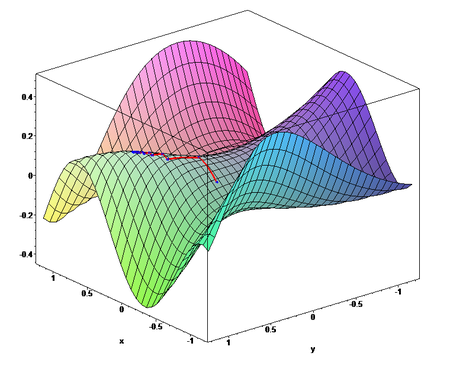
Application de la méthode de remontée de gradient à la fonction
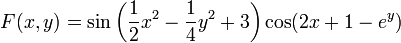 :
: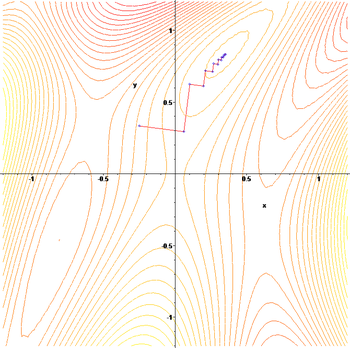 Vue en plan avec lignes de niveaux.
Vue en plan avec lignes de niveaux.
Quelques précisions
La descente de gradient peut s'appliquer à des espaces de dimension quelconque, même pour des espaces de dimension infinie. Dans ce dernier cas, l'espace de recherche est l'espace des fonctions, et la direction de descente est déterminée en calculant la dérivée de Gâteaux de la fonctionnelle à minimiser.
Deux points faibles de la descente de gradient sont :
- L'algorithme peut nécessiter de nombreuses itérations pour converger vers un minimum local, notamment si la courbure est très différente dans des directions différentes.
- La recherche du pas γ optimal, généralement effectuée par une recherche linéaire, peut se révéler très longue. Inversement, utiliser un pas γ fixe peut conduire à de mauvais résultats. Des méthodes comme la méthode de Newton et l'inversion de la matrice hessienne en complément des techniques de gradient conjugué sont souvent de meilleures alternatives.
Un algorithme plus puissant est la méthode BFGS, qui consiste à calculer en chaque étape une matrice, qui multipliée au gradient permet d'obtenir une meilleure direction. De plus, cette méthode peut être combinée avec une méthode plus efficace de recherche linéaire afin d'obtenir la meilleure valeur de γ.
La descente de gradient correspond en fait à la méthode d'Euler de résolution d'équations différentielles ordinaires appliquée à un flot de gradient. Comme le but est de trouver le minimum et non la ligne de flot, l'erreur commise est moins significative.
Un exemple numérique
La descente de gradient est ici appliquée afin de trouver le minimum de la fonction f(x) = x4 − 3x3 + 2, dont la dérivée est f'(x) = 4x3 − 9x2. Voici un exemple d'implémentation de la descente de gradient sur cette fonction en langage C.
#include <stdio.h> #include <stdlib.h> #include <math.h> int main () { // Analytiquement, on peut déterminer qu'un minimum local de la fonction est trouvé pour x=9/4 // L'algorithme commence à x=6 double xOld = 0; double xNew = 6; double eps = 0.01; // taille du pas fixe double precision = 0.00001; while (fabs(xNew - xOld) > precision) { xOld = xNew; xNew = xNew - eps*(4*xNew*xNew*xNew-9*xNew*xNew); } printf ("Le minimum local est obtenu pour x = %lg\n", xNew); }
Avec la précision choisie ici, l'algorithme converge vers un minimum situé en x = 2.24996 en 70 itérations.
Une implémentation plus robuste que celle-ci pourrait incorporer une méthode de recherche linéaire du meilleur pas ; ou, plus simplement vérifier si la valeur de la fonction diminue bien à chaque itération et dans le cas contraire diminuer la valeur du pas de déplacement γ. Une recherche linéaire du meilleur pas permettrait à l'algorithme de converger plus rapidement.
Voir aussi
- Gradient
- Analyse vectorielle
- Recherche linéaire
- Méthode de Newton
- Descente de gradient stochastique
- Optimisation
- Critères de Wolfe
Références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Gradient descent ».
- Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Publishing. ISBN 0-387-24348-8
- Portail des mathématiques
Catégories : Analyse à plusieurs variables | Algorithme d'optimisation
Wikimedia Foundation. 2010.