Algorithme de levenberg-marquardt

L’algorithme de Levenberg-Marquardt, ou algorithme LM, permet d'obtenir une solution numérique au problème de minimisation d'une fonction, souvent non-linéaire et dépendant de plusieurs variables. L'algorithme interpole l'algorithme de Gauss-Newton et la méthode de descente de gradient. Plus stable que celui de Gauss-Newton, il trouve une solution même s'il est démarré très loin d'un minimum. Cependant, pour certaines fonctions très régulières, il peut converger légèrement moins vite. L'algorithme fut découvert par Kenneth Levenberg, puis publié par Donald Marquardt.

C'est un problème qui se présente souvent en régression linéaire et non-linéaire.

Sommaire 1 Application à la méthode des moindres carrés 1.1 Énoncé 1.2 Solution 2 Choix du paramètre d'amortissement 3 Notes et références 4 Voir aussi 4.1 Articles connexes 4.2 Liens externes 4.2.1 Descriptions de l'algorithme 4.2.2 Mises en œuvres 4.3 Sources

Application à la méthode des moindres carrés

Énoncé

Son application principale est la régression au travers de la méthode des moindres carrés : étant donné un certain nombre de paires de données (t_i, y_i), on cherche le paramètre a de la fonction f(t|a) de sorte que la somme des carrés des déviations :

soit minimale.

Solution

La procédure de l'algorithme est itérative. On part d'un paramètre initial, que l'on suppose « assez proche » d'un minimum, et qui constituera le vecteur p de départ. Dans beaucoup de cas, un paramètre de départ « standard » , tel que p^T=(1,1,...,1) fonctionnera sans problèmes. Dans certains cas, il n'y a convergence que si le vecteur de départ n'est pas trop éloigné de la solution.

À chaque itération, on remplace p par une nouvelle estimation p + q. Afin de déterminer q, les fonctions f_i(p + q) sont approchées en étant linéarisées :

f(p + q) ≈ f(p) + Jq

où on a noté J le Jacobien de f en p.

À un minimum de la somme des carrés S, on a 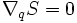. En dérivant le carré de l'expression de droite, qui s'annule donc, on obtient :

(J^TJ)q = J^T[y − f(p)]

d'où l'on tire aisément q en inversant J^TJ. Le point essentiel de l'algorithme de Levenberg-Marquardt est d'approcher cette équation, en l' « amortissant » un peu :

(J^TJ + λ.I)q = J^T[y − f(p)].

Le facteur d'amortissement positif λ est ajusté à chaque nouvelle itération. Si la diminution de S est rapide, on peut utiliser une valeur plus faible - ce qui rapproche l'algorithme de celui de Gauss-Newton. Si en revanche une itération est peu efficace, on peut augmenter λ - ce qui rapproche cette fois l'algorithme de celui de descente de gradient. Un tel facteur d'amortissement est utilisé par exemple dans la régularisation de Tikhonov, utilisée pour résoudre certains problèmes linéaires.

Si on a effectué plus d'un certain nombre d'itérations, ou bien que l'on s'est approché suffisamment d'un minimum, la procédure se termine et renvoie le paramètre p comme estimation de la solution.

Choix du paramètre d'amortissement

De nombreux arguments, plus ou moins heuristiques ont été proposés afin de déterminer le meilleur facteur d'amortissement λ. Des démonstrations théoriques montrent que certains choix garantissent une convergence locale - mais peuvent afficher une convergence faible près de l'optimum.

La valeur absolue de tout choix dépend de l'échelle du problème. Marquardt recommandait de commencer à partir de λ₀ et avec un facteur ν>1. On pose alors au départ λ=λ₀ et calculons la somme des carrés des déviations S(p) après une itération, en utilisant le facteur d'amortissement λ=λ₀, puis en utilisant λ/ν. Si les deux derniers renvoient un point moins bon que le point de départ, on augmente λ en le multipliant par ν, jusqu'à atteindre un point meilleur avec un nouveau facteur λν^k pour un certain k.

Si l'utilisation du facteur λ/ν donne une somme plus faible, alors il est pris comme nouvelle valeur de λ et l'algorithme continue. Si l'utilisation de λ/ν donne une somme plus importante, mais que l'utilisation de λ donne une somme plus faible, alors λ est conservé.

Notes et références

Voir aussi

Articles connexes

• Régularisation Tychonoff

Liens externes

Descriptions de l'algorithme

• (en) « Numerical Recipes in C », Chapitre 15.5 : Modèles non-linéaires, avec une description de l'algorithme ;
• (en) Histoire de l'algorithme ;
• (en) Tutoriel écrit par Ananth Ranganathan.

Mises en œuvres

• (en) lmdif, implémentation classique en Fortran, domaine publique.
• (en) lmfit, translation de lmdif en C/C++, enveloppe pour régression, avec exemple d'application, domaine publique.
• (en) levmar, implémentation GPL en C++, Perl et Python.
• (en) [1] et [2] : mises en œuvres Java.
• (en) gnuplot en possède une implémentation.
• (en) ALGLIB, implémentations en C#, C++, Delphi, Visual Basic.
• (fr) FitOO, implémentation sous forme de modèle et de macros pour OpenOffice.org.
• (fr) IMSL, implémentation pour Fortran, C/C++, Java et C#.
• (en) Mathworks: LMFsolve.m/LMFnlsq.m, implémentation pour Matlab.

Sources

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Levenberg-Marquardt algorithm ».
• Levenberg, K. « A Method for the Solution of Certain Problems in Least Squares. » Quart. Appl. Math. 2, 164-168, 1944.
• Marquardt, D. « An Algorithm for Least-Squares Estimation of Nonlinear Parameters. » SIAM J. Appl. Math. 11, 431-441, 1963.
• Gill, P. E. and Murray, W. « Algorithms for the solution of the nonlinear least-squares problem », SIAM J. Numer. Anal. 15 [5] 977-992, 1978.

• Portail de l’informatique