Idéal Principal

Idéal Principal

Idéal principal

En mathématiques, plus particulièrement dans la théorie des anneaux, un idéal principal est un idéal engendré par un unique élément.

Sommaire

Définition

Soit A un anneau. Soit I un idéal de A.

  • I est dit principal à gauche s'il existe un élément 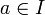a\in I tel que, pour tout 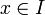x\in I, il existe un élément 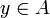y\in A tel que x = y.a : 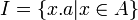I=\{x.a|x\in A\}. On note I = Aa.
  • I est dit principal à droite s'il existe un élément 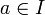a\in I tel que, pour tout 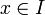x\in I, il existe un élément 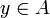y\in A tel que x = a.y : 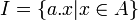I=\{a.x|x\in A\} On note I = aA.

I est dit principal s'il est principal à la fois à gauche et à droite (ce qui est toujours le cas si A est commutatif). Dans ce cas, on peut noter I = a.A et I est forcément le plus petit idéal contenant a.

Exemples

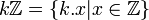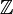Pour tout entier relatif k, k\mathbb Z=\{k.x|x\in\mathbb Z\} est un idéal principal de \mathbb Z.

Un idéal n'est pas forcément principal. Par exemple, si A=\mathbb C[X,Y], l'anneau commutatif des polynômes à deux indéterminées à coefficients complexes, l'ensemble des polynômes ayant un terme constant nul, noté (X,Y) car engendré par ces deux variables, est un idéal de \mathbb C[X,Y], mais il n'est pas principal : si P engendrait (X,Y), X et Y seraient divisibles par P, ce qui est impossible, sauf si P est un polynôme constant non-nul, ce qui est contradictoire.

Anneau principal

Un anneau intègre dont tous les idéaux sont principaux est dit anneau principal.

Par exemple, 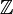\mathbb Z ou l'anneau \mathbb K[X] des polynômes sur un corps \mathbb K sont des anneaux principaux.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Id%C3%A9al principal ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Idéal Principal de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Ideal principal — Idéal principal En mathématiques, plus particulièrement dans la théorie des anneaux, un idéal principal est un idéal engendré par un unique élément. Sommaire 1 Définition 2 Exemples 3 Anneau principal …   Wikipédia en Français

  • Idéal principal — En mathématiques, plus particulièrement dans la théorie des anneaux, un idéal principal est un idéal engendré par un unique élément. Définition Soit A un anneau. Soit I un idéal de A. I est dit principal à gauche s il existe un élément tel que,… …   Wikipédia en Français

  • Ideal principal — Este artículo está huérfano, pues pocos o ningún artículo enlazan aquí. Por favor, introduce enlaces hacia esta página desde otros artículos relacionados …   Wikipedia Español

  • Theoreme de l'ideal principal — Théorème de l idéal principal Soit K un corps de nombres. Les extensions abéliennes, et les extensions non ramifiées, sont stables par compositum. Il existe donc une extension abélienne non ramifiée maximale de K, elle est appelée corps de… …   Wikipédia en Français

  • Théorème de l'idéal principal —  Ne doit pas être confondu avec Théorème des idéaux principaux de Krull. En mathématiques, le théorème de l idéal principal en théorie des corps de classes, assure que tout idéal de l anneau des entiers d un corps de nombres K, vu comme… …   Wikipédia en Français

  • Idéal de l'anneau des entiers d'un corps quadratique — En mathématiques et plus précisément en théorie algébrique des nombres, l anneau des entiers d un corps quadratique ressemble à certains égards à celui des entiers relatifs. Certains d entre eux sont euclidiens comme celui des entiers de Gauss d… …   Wikipédia en Français

  • Idéal — Pour les articles homonymes, voir Idéal (homonymie). En mathématiques, et plus particulièrement en algèbre, un idéal est un sous ensemble remarquable d un anneau. Par certains égards, les idéaux s apparentent aux sous espaces vectoriels ce sont… …   Wikipédia en Français

  • Idéal fractionnaire — Richard Dedekind donne en 1876 la définition d idéal fractionnaire. En mathématiques, et plus précisément en théorie des anneaux, un idéal fractionnaire est une généralisation de la définition d un idéal. Ce concept doit son origine à la théorie… …   Wikipédia en Français

  • Ideal (teoría de anillos) — En matemáticas, un ideal es una estructura algebraica definida en un anillo. Los ideales generalizan de manera fecunda el estudio de la divisibilidad en los números enteros. De este modo, es posible enunciar versiones muy generales de teoremas… …   Wikipedia Español

  • Ideal premier — Idéal premier Richard Dedekind 1831 1916 formalisateur du concept d idéal Un idéal premier est un concept associé à la théorie des anneaux en mathématiques et plus précisément en algèbre. Un idéal d un anneau commutatif unitaire est dit premier… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”