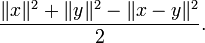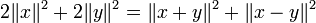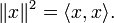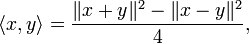Identité du parallélogramme
- Identité du parallélogramme
-
Règle du parallélogramme
En mathématiques, la forme la plus simple de la règle du parallélogramme est celle de géométrie élémentaire. Elle dit que la somme des carrés des longueurs des quatre cotés d'un parallélogramme est égale à la somme des carrés des longueurs de ses diagonales. Dans le cas où le parallélogramme est un rectangle, les diagonales sont de longueurs égales ce qui ramène cette règle au théorème de Pythagore
La règle du parallélogramme dans les espaces préhilbertiens
Dans les espaces préhilbertiens, la règle du parallélogramme revient à cette identité algébrique :
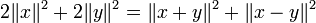
où
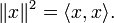
Elle est vérifiée pour tous les espaces de Hilbert.
Espaces normés satisfaisant la règle du parallélogramme
Beaucoup d'espaces vectoriels normés n'ont pas de produit scalaire mais comme ils ont une norme, ils peuvent évaluer tous les termes de l'identité précédente de la règle du parallélogramme. Un fait remarquable est que l'identité reste valide seulement si la norme est une norme qui se déduit d'un produit scalaire. De plus le produit scalaire qui génère cette norme est unique, par la conséquence de l'identité de polarisation. Dans le cas réel il est donné par :
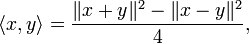
ou de manière équivalente :
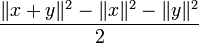 ou
ou 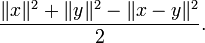
Dans le cas complexe il est donné par:
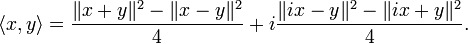
 Portail des mathématiques
Portail des mathématiques
Catégories : Algèbre bilinéaire | Géométrie euclidienne
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Identité du parallélogramme de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Identite de polarisation — Identité de polarisation En mathématiques, l identité de polarisation concerne l algèbre bilinéaire. Elle correspond à une caractérisation des formes symétriques, bilinéaires ou sesquilinéaires. Si E est un espace vectoriel ces formes sont des… … Wikipédia en Français
Identité De Polarisation — En mathématiques, l identité de polarisation concerne l algèbre bilinéaire. Elle correspond à une caractérisation des formes symétriques, bilinéaires ou sesquilinéaires. Si E est un espace vectoriel ces formes sont des applications de ExE dans le … Wikipédia en Français
Identité de polarisation — En mathématiques, les identités de polarisation concernent l algèbre multilinéaire. Elles correspondent à une caractérisation des formes bilinéaires symétriques, des formes hemitiennes et des formes sesquilinéaires. Si E est un espace vectoriel,… … Wikipédia en Français
Identité de Lagrange — En mathématiques, et plus particulièrement en algèbre, l’identité de Lagrange, découverte par Joseph Louis Lagrange, est une formule transformant un produit de sommes de carrés en une autre somme de carrés ; elle a d importantes conséquences … Wikipédia en Français
Règle du parallélogramme — En mathématiques, la forme la plus simple de la règle du parallélogramme est celle de géométrie élémentaire. Elle dit que la somme des carrés des longueurs des quatre côtés d un parallélogramme est égale à la somme des carrés des longueurs de ses … Wikipédia en Français
Regle du parallelogramme — Règle du parallélogramme En mathématiques, la forme la plus simple de la règle du parallélogramme est celle de géométrie élémentaire. Elle dit que la somme des carrés des longueurs des quatre cotés d un parallélogramme est égale à la somme des… … Wikipédia en Français
Espace Préhilbertien — En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la dimension finie. Le cas… … Wikipédia en Français
Espace prehilbertien — Espace préhilbertien En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la… … Wikipédia en Français
Espace préhilbertien — En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la dimension finie. Sommaire 1… … Wikipédia en Français
Espace Vectoriel Normé — Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très… … Wikipédia en Français
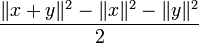 ou
ou