Identité De Polarisation

Identité de polarisation

En mathématiques, l'identité de polarisation concerne l'algèbre bilinéaire. Elle correspond à une caractérisation des formes symétriques, bilinéaires ou sesquilinéaires. Si E est un espace vectoriel ces formes sont des applications de ExE dans le corps de nombres sous-jacent. Elles sont intégralement caractérisées par leur comportement sur la diagonale, c'est-à-dire par la connaissance d'une telle forme φ sur l'ensemble des points (x, x) où x est un élément quelconque de E. L'application qui à x associe φ(x, x) est la forme quadratique associée. Il existe ainsi une équivalence entre les formes quadratiques et les formes symétriques.

Une identité de polarisation permet d'exprimer la forme bilinéaire à partir de la forme quadratique.

Sommaire

1 Identités de polarisation
- 1.1 Forme bilinéaire
- 1.2 Forme sesquilinéaire
2 Propriété
- 2.1 Cas réel
- 2.2 Cas complexe
3 Références et notes

Identités de polarisation

Les Identités de polarisation sont de deux types différents, celles qui s'appliquent sur les formes bilinéaires et celles pour les formes sesquilinéaires.

Forme bilinéaire

Le contexte de l'identité de polarisation est celui d'un espace vectoriel E quelconque sur un corps K quelconque. Soit φ une forme quadratique sur E, non nécessairement définie et non nécessairement positive.

Définition — On appelle identité polaire, une des deux égalités suivantes, définissant une forme symétrique ψ de ExE dans K :

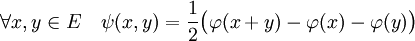
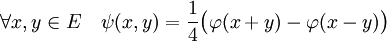
$\forall x,y\in E\quad \psi(x,y) = \frac12\bigl(\varphi(x+y)-\varphi(x)-\varphi(y)\bigr)$ $\forall x,y\in E\quad \psi(x,y) = \frac14\bigl(\varphi(x+y)-\varphi(x-y)\bigr)$

En particulier, soit E un espace préhilbertien réel dont la norme d'un vecteur x est notée : 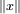$\scriptstyle {\|x\|}$ et le produit scalaire de deux vecteurs x et y : 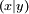$\scriptstyle {(x|y)}$ . Les deux égalités suivantes sont vérifiées :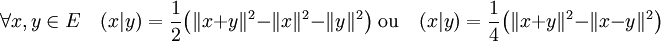

$\forall x,y \in E \quad (x|y) = \frac12\bigl(\|x+y\|^2-\|x\|^2-\|y\|^2\bigr)\;\text{ou}\quad (x|y)= \frac14 \bigl( \|x+y\|^2 -\|x-y\|^2\bigr)$

Ces résultats proviennent de la propriété suivante, si ψ est une forme bilinéaire de ExE quelconque :

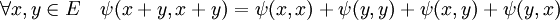
$\forall x,y\in E\quad \psi(x+y,x+y) = \psi(x,x) + \psi(y,y) + \psi(x,y) + \psi(y,x)$

Et l'application qui à (x, y) associe ½(ψ(x, y) + ψ(y, x)) est symétrique.

Forme sesquilinéaire

Si le corps K sous-jacent à E n'est pas totalement ordonné, il n'est pas possible, dans le cas général, de définir l'équivalent d'une norme associée à une distance. Il existe néanmoins une solution si K est l'ensemble des nombres complexes. La forme doit alors être choisie sesquilinéaire. Dans ce paragraphe E est un espace vectoriel complexe :

Définition — On appelle identité polaire, l' égalité suivante, définissant une forme sesquilinéaire symétrique ψ de ExE dans C :

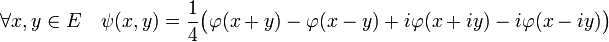
$\forall x,y\in E\quad \psi(x,y) = \frac14\bigl(\varphi(x+y)-\varphi(x-y)+ i\varphi(x+iy)-i\varphi(x-iy)\bigr)$

Ici i désigne le nombre imaginaire pur. La remarque précédente s'applique encore, si E est un espace préhilbertien complexe et avec les notations du paragraphe précédent :

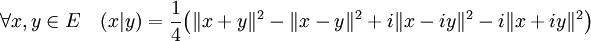
$\forall x,y \in E \quad (x|y) = \frac14 \bigl( \|x+y\|^2 -\|x-y\|^2 + i\|x-iy\|^2 -i\|x+iy\|^2\bigr)$

Propriété

L'application qui, à une forme bilinéaire (resp. sesquilinéaire) associe sa forme quadratique est un isomorphisme. La forme polaire correspond à l'isomorphisme réciproque.

Il est possible d'aller plus loin à l'aide de la règle du parallélogramme.

Cas réel

Dans ce paragraphe E désigne un espace vectoriel réel. Si φ est une forme quadratique, elle vérifie l'égalité suivante dite, règle du parallélogramme :

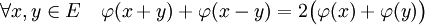
$\forall x,y \in E \quad \varphi(x+y) + \varphi(x-y) = 2\bigl( \varphi(x) + \varphi(y)\bigr)$

Il est naturel de se poser la question de savoir ce qu'il en est d'une norme quelconque satisfaisant cette égalité :

Théorème de Fréchet-Von Neumann-Jordan cas réel^[1] — Soit N une norme de E. N dérive d'un produit scalaire si et seulement si elle respecte l'identité du parallélograme. Le produit scalaire conférant à E le statut d'espace préhilbertien de norme N est donné par l'identité de polarisation.

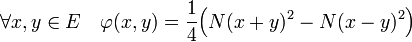
$\forall x,y \in E \quad \varphi (x,y) = \frac 14 \Big( N(x+y)^2 -N(x-y)^2 \Big)$

Il n'est pas nécessaire d'imposer à N d'être une norme. Il suffit qu'elle soit strictement positive sur tout vecteur de E non nul, nulle pour le vecteur nul et continue.

La démonstration ne fait pas appel au caractère fini de la dimension de E. Elle est donc parfaitement générale.

Démonstration

Si λ est un scalaire et x un vecteur de E, alors :

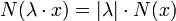
$N(\lambda \cdot x) = |\lambda |\cdot N(x)$

Montrons dans un premier temps que l'image de -x par N est celle de x :

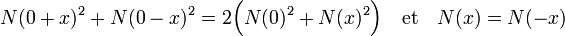
$N(0 + x)^2 + N(0 -x)^2 = 2\Big( N(0)^2 + N(x)^2\Big)\quad \text{et}\quad N(x) = N(-x)$

On vérifie que N(0.x) est égal à zéro, N(1.x) est égal à N(x) et par récurrence, N(n.x) =n.N(x) en effet :

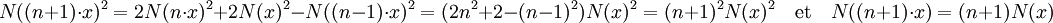
$N((n+1)\cdot x)^2 = 2N(n\cdot x)^2 + 2N(x)^2 -N((n-1)\cdot x)^2=(2n^2+2-(n-1)^2)N(x)^2=(n+1)^2N(x)^2\quad \text{et}\quad N((n+1)\cdot x)=(n+1)N(x)\;$

Si y est égal à n.x, alors les résultats précédents montrent que :

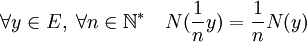
$\forall y \in E,\; \forall n \in \mathbb N^* \quad N(\frac 1ny)=\frac 1n N(y)$

Les trois derniers résultats montrent que :

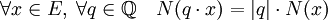
$\forall x \in E,\; \forall q \in \mathbb Q \quad N(q\cdot x)=|q|\cdot N(x)$

La continuité de N, ainsi que le fait que l'ensemble des nombres rationnels est dense dans R montre le résultat recherché.

Si x et y sont deux vecteurs de E tel que N(x + y)² = N(x)² + N(x)², alors pour tout λ et $μ$ réels, N(λx + μy)² = λ²N(x)² + μ²N(x)² :

Si λ est nul, la proposition est une conséquence directe de la proposition précédente. Montrons que la proposition est vraie si λ est égal à un. Elle est vraie si μ est égal à zéro ou un. Supposons qu'elle est vraie jusqu'à p et montrons-la pour p + 1:

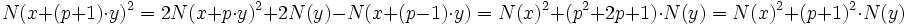
$N(x + (p+1)\cdot y)^2 = 2N(x + p\cdot y)^2 +2N(y) -N(x+(p-1)\cdot y)=N(x)^2+(p^2+2p+1)\cdot N(y)=N(x)^2+(p+1)^2\cdot N(y)$

Ce qui montre le résultat par récurrence. Un raisonnement analogue au précédent montre que le résultat est vrai pour tout réel. Si λ est différent de zéro:

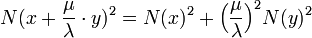
$N(x + \frac{\mu}{\lambda}\cdot y)^2=N(x)^2+\Big(\frac{\mu}{\lambda}\Big)^2N(y)^2$

On en déduit :

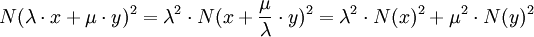
$N(\lambda\cdot x + \mu \cdot y)^2 = \lambda^2\cdot N(x + \frac{\mu}{\lambda}\cdot y)^2= \lambda^2\cdot N(x)^2+ \mu^2 \cdot N(y)^2$

L'expression de l'application N est donc simple dans le cas où x et y sont orthogonaux c'est-à-dire si le carré de l'image de la somme de x et y est égal à la somme des carrés des images.

Si x et y forment une famille libre, alors il existe deux vecteurs orthogonaux et normés e₁ et e₂ tel que l'espace engendré par ces deux vecteurs contient x et y :

le vecteur x est non nul car il appartient à une famille libre. Soit e₁ le vecteur égal à 1/N(x).x. Considérons l'application f du segment [-1, 1] dans E définie par :

$\forall \lambda \in [-1,1] f(\lambda)= \lambda e_1 + (1 - \lambda^2)y$

Considérons la fonction g du segment [-1, 1] dans R définie par :

$\forall \lambda \in [-1,1] \quad g(\lambda)=\varphi (e_1,f(\lambda))$

Ici φ désigne l'identité polaire associée à la fonction N :

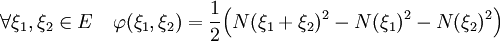
$\forall \xi_1,\xi_2 \in E \quad \varphi(\xi_1,\xi_2)=\frac 12 \Big(N(\xi_1+\xi_2)^2-N(\xi_1)^2 -N(\xi_2)^2\Big)$

La fonction g est continue, de plus g(-1) = -1 et g(1) = 1, il existe donc une valeur λ₀ tel que g(λ₀) est égal à zéro. Définissons e₂ comme un vecteur normalisé et colinéaire à f(λ₀). La proposition précédente montre que la famille (e₁, e₂) vérifie les propriétés requises.

L'application φ est bilinéaire symétrique définie positive si E est de dimension deux :

La proposition précédente montre l'existence d'une base (e₁, e₂) orthonormée. Soit x (resp. y) un vecteur de E, Soit α₁ et α₂ (resp. β₁, β₂) les coordonnées de x (resp. y) dans la base, alors :

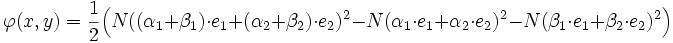
$\varphi(x,y)= \frac 12\Big(N((\alpha_1+\beta_1)\cdot e_1+(\alpha_2 + \beta_2)\cdot e_2)^2-N(\alpha_1\cdot e_1+\alpha_2\cdot e_2)^2-N(\beta_1\cdot e_1+\beta_2\cdot e_2)^2\Big)$

La deuxième proposition montre que :

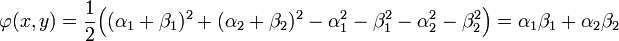
$\varphi(x,y)=\frac 12\Big((\alpha_1+\beta_1)^2 + (\alpha_2 + \beta_2)^2 -\alpha_1^2 -\beta_1^2-\alpha_2^2 -\beta_2^2\Big) = \alpha_1\beta_1 + \alpha_2\beta_2$

La dernière égalité montre le caractère bilinéaire et symétrique de l'application φ. Le carré de N est bien la forme quadratique associée, ce qui montre le caractère défini positif.

L'application φ est bilinéaire symétrique définie positive :

Soit x₁, x₂ et y trois éléments de E et λ un scalaire. Montrons que :

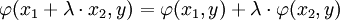
$\varphi(x_1 + \lambda\cdot x_2,y)=\varphi(x_1,y)+\lambda\cdot \varphi(x_2,y)$

Si les trois vecteurs sont liées la proposition précédente permet de conclure car sur l'espace engendré par les trois vecteurs, φ est bilinéaire symétrique. Sinon, soit x le vecteur x₁ + λ.x₂ et (f₁, f₂) une base orthonormale de l'espace vectoriel engendré par x et y tel que f₁ et x₁ soient colinéaires. Alors φ est bien une application bilinéaire définie positive dans l'espace engendré par x et y, on en déduit :

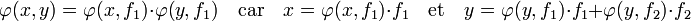
$\varphi(x,y)=\varphi(x,f_1)\cdot \varphi(y,f_1)\quad \text{car}\quad x=\varphi(x,f_1)\cdot f_1\quad \text{et}\quad y=\varphi(y,f_1)\cdot f_1+\varphi(y,f_2)\cdot f_2$

Comme x et f₁ sont colinéaires et que x est combinaison linéaire de x₁ et x₂, ces quatre vecteurs sont dans un espace vectoriel de dimension deux. La restriction de φ à cet espace est bilinéaire symétrique, donc :

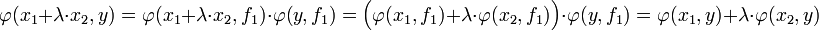
$\varphi(x_1 + \lambda\cdot x_2,y)=\varphi(x_1 + \lambda\cdot x_2,f_1)\cdot \varphi(y,f_1)= \Big(\varphi(x_1,f_1)+ \lambda\cdot \varphi(x_2,f_1)\Big)\cdot \varphi(y,f_1)= \varphi(x_1,y)+\lambda\cdot \varphi(x_2,y)$

Le caractère symétrique de φ provient de la définition d'une forme polaire, φ est définie positive car N² est sa forme quadratique associée.

Cas complexe

Dans ce paragraphe E désigne un espace vectoriel complexe. L'identité du parallélogramme est encore valable,

La situation est ici encore analogue à celle des espaces réels. La norme d'un produit hermitien le caractérise. Réciproquement une norme N satisfaisant la règle du parallélogramme est issue d'un produit scalaire. Ce résultat n'est pas uniquement vrai en dimension finie. Toute norme satisfaisant l'égalité du parallélogramme est issue d'un produit scalaire.

Théorème de Fréchet-Von Neumann-Jordan cas complexe — Soit N une norme de E. N dérive d'un produit scalaire si et seulement si elle respecte l'identité du parallélograme. Le produit hermitien correspond alors à l'identité de polarisation et confère à E le statut d'espace préhilbertien de norme N.

Comme précédemment, la démonstration ne fait pas appel au caractère fini de la dimension de E.

Démonstration

La logique est analogue à celle du cas réel. Dans un premier temps on montre que ce résultat est vrai en dimension un, puis deux puis dans le cas général. Comme le cas réel est déjà traité (la démonstration est donnée dans l'article Espace euclidien), si E est considéré comme un espace vectoriel réel noté E_R il est équipé d'un produit scalaire <.,.>_R dont la norme dérive.

Le résultat est vrai si la dimension de E est égale à un .

Soit e₁ un vecteur de norme égal à un. Soit λe₁ et μe₁ deux vecteurs quelconques de E. Définissons le produit scalaire complexe <.,.>_C par :

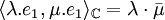
$\langle \lambda.e_1,\mu.e_1\rangle_{\mathbb C} = \lambda\cdot \bar\mu$

Comme N est une norme et que N(e₁) est égal à un, le produit scalaire précédent convient.

Le résultat est vrai si la dimension de E est égale à deux :

Soit e₁ un vecteur défini comme précédemment. Remarquons que e₁ et i.e₁ sont orthonormaux pour <.,.>_R. En effet :

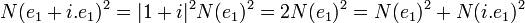
$N(e_1+i.e_1)^2= |1+i|^2N(e_1)^2= 2N(e_1)^2= N(e_1)^2 + N(i.e_1)^2\;$

Le théorème de Pythagore est vérifié sur les vecteurs e₁ et i.e₁, ce qui montre qu'ils sont orthogonaux pour le produit scalaire <.,.>_R. Ce résultat est vrai pour les produits scalaires réels mais faux dans le cas complexe. Soit f l'application de E_R qui au vecteur a associe i.a. La fonction f est un endomorphisme de E_R, c'est de plus une isométrie donc un automorphisme orthogonal. L'espace vectoriel E_1R engendré par e₁ et i.e₁ est stable par f, son orthogonal pour <.,.>_R est stable par f, en effet, soit y un élément de l'orthogonal. Comme f est une isométrie et que f² est égal à l'homothétie de rapport -1 :

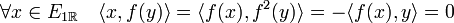
$\forall x \in E_{1\mathbb R} \quad \langle x,f(y)\rangle=\langle f(x),f^2(y)\rangle=-\langle f(x),y\rangle=0$

Il suffit en effet de remarquer que f(x) est élément de E_1R et donc qu'il est orthogonal à y. Cette propriété est générique à tous les endomorphismes normaux. Soit e₂ un vecteur de l'orthogonal de E_1R et de norme un. On remarque que la famille (e₁, i.e₁, e₂, i.e₂) est une base orthonormale de E_R. Définissons <.,.>_C comme le produit scalaire tel que la base (e₁, e₂) soit orthonormale. Soit x un vecteur quelconque de E. Alors il existe quatre réels α₁, α₂, β₁ et β₂ tel que :

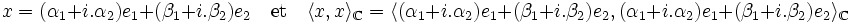
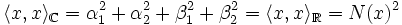
$x=(\alpha_1 + i.\alpha_2)e_1 + (\beta_1 + i.\beta_2)e_2 \quad \text{et}\quad \langle x,x\rangle_{\mathbb C} = \langle (\alpha_1 + i.\alpha_2)e_1 + (\beta_1 + i.\beta_2)e_2,(\alpha_1 + i.\alpha_2)e_1 + (\beta_1 + i.\beta_2)e_2\rangle_{\mathbb C}$ $\langle x,x\rangle_{\mathbb C} = \alpha_1^2 + \alpha_2^2 + \beta_1^2 + \beta_2^2 = \langle x,x\rangle_{\mathbb R}=N(x)^2$

L'unicité provient du fait que ce produit scalaire est aussi donnée par la forme polaire.

Le résultat est vrai quelle que soit la dimension de E :

La démonstration est calquée sur celle des espaces euclidiens. Soit φ l'application de ExE dans R définie par :

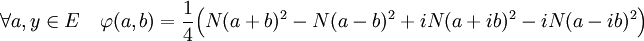
$\forall a,y \in E \quad \varphi(a,b)=\frac14\Big(N(a+b)^2 - N(a-b)^2 + iN(a+ib)^2 - iN(a-ib)^2\Big)$

Soit x₁, x₂ et y trois éléments de E et λ un nombre complexe. Montrons que :

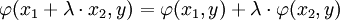
$\varphi(x_1 + \lambda\cdot x_2,y)=\varphi(x_1,y)+\lambda\cdot \varphi(x_2,y)$

Si les trois vecteurs sont liées la proposition précédente permet de conclure car sur l'espace engendré par les trois vecteurs, φ est un produit scalaire. Sinon, soit x le vecteur x₁ + λ.x₂ et (f₁, f₂) une base orthonormale de l'espace vectoriel engendré par x et y tel que f₁ et x₁ soient colinéaires. Alors φ est un produit scalaire sur l'espace vectoriel engendré par x et y d'après la proposition précédente. Un calcul à l'aide des coefficients de Fourier sur la base orthonormale permet de montrer que :

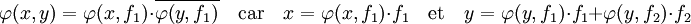
$\varphi(x,y)=\varphi(x,f_1)\cdot \overline {\varphi(y,f_1)}\quad \text{car}\quad x=\varphi(x,f_1)\cdot f_1\quad \text{et}\quad y=\varphi(y,f_1)\cdot f_1+\varphi(y,f_2)\cdot f_2$

Comme x et f₁ sont colinéaires et que x est combinaison linéaire de x₁ et x₂, ces quatre vecteurs sont dans un espace vectoriel de dimension deux. La restriction de φ à cet espace est un produit scalaire, donc :

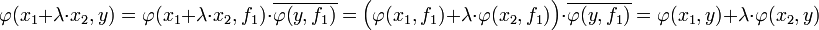
$\varphi(x_1 + \lambda\cdot x_2,y)=\varphi(x_1 + \lambda\cdot x_2,f_1)\cdot\overline{\varphi(y,f_1)} = \Big(\varphi(x_1,f_1)+ \lambda\cdot \varphi(x_2,f_1)\Big)\cdot\overline{\varphi(y,f_1)}= \varphi(x_1,y)+\lambda\cdot \varphi(x_2,y)$

Un calcul analogue montre que le produit est antilinéaire par rapport à la deuxième variable. Le caractère symétrique défini positif provient du fait que la forme sesquilinéaire dérive de la forme polaire d'une norme.^[2]

Références et notes

Notes

↑ Cette dénomination est indiquée dans : Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] p 87
↑ Cette démonstration se trouve aussi dans la référence précédente

Référence

Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
K. Yosida Functional Analysis Springer 1980 (ISBN 3-540-10210-8)

Liens externes

(fr) Forme quadratique,polarisation par V. et F. Bayart dans Bibmath.net
(fr) Espaces préhilbertiens par C.Antonini, J.F. Quint, P. Borgnat, J. Bérard, E. Lebeau, E. Souche, A. Chateau, O. Teytaud dans les les mathématiques.net 2001

Ce document provient de « Identit%C3%A9 de polarisation ».

Catégories : Algèbre bilinéaire | Identité mathématique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Identité De Polarisation de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Identite de polarisation — Identité de polarisation En mathématiques, l identité de polarisation concerne l algèbre bilinéaire. Elle correspond à une caractérisation des formes symétriques, bilinéaires ou sesquilinéaires. Si E est un espace vectoriel ces formes sont des… … Wikipédia en Français
Identité de polarisation — En mathématiques, les identités de polarisation concernent l algèbre multilinéaire. Elles correspondent à une caractérisation des formes bilinéaires symétriques, des formes hemitiennes et des formes sesquilinéaires. Si E est un espace vectoriel,… … Wikipédia en Français
Identité du parallélogramme — Règle du parallélogramme En mathématiques, la forme la plus simple de la règle du parallélogramme est celle de géométrie élémentaire. Elle dit que la somme des carrés des longueurs des quatre cotés d un parallélogramme est égale à la somme des… … Wikipédia en Français
Identité idéologique — Idéologie Une idéologie est au sens large, la science d un système d idées imaginées. L idéologie s accompagne de notions, d opinions, de convictions et est parfois constitués en doctrine. Pour Karl Marx, l idéologie sert de masque à la… … Wikipédia en Français
Espace hermitien — Charles Hermite en 1887 En mathématiques, un espace hermitien est un espace vectoriel sur le corps commutatif des complexes de dimension finie et muni d un produit scalaire. La géométrie d un tel espace est analogue à celle d un espace euclidien … Wikipédia en Français
Espace Euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… … Wikipédia en Français
Espace euclidien (algèbre linéaire) — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique … Wikipédia en Français
Espaces euclidiens — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique … Wikipédia en Français
Espace euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… … Wikipédia en Français
Espace Préhilbertien — En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la dimension finie. Le cas… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Identité De Polarisation