Hexagramme de pascal

Hexagramme de pascal

Hexagramme de Pascal

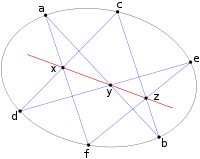
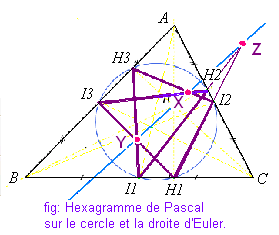
Page d'aide sur l'homonymie Pour les articles homonymes, voir Hexagramme.
Hexagrammum Mysticum.svg

L'hexagramme de Pascal, ou hexagramme mystique, est une figure géométrique illustrant le théorème de Pascal. Il représente un hexagone quelconque inscrit dans une conique. Ce théorème démontre que les trois intersections des côtés opposés sont alignées.

Plus précisément : les trois intersections sont alignées, si, et seulement si, les six points sont sur une conique et le plan de projection est pappusien.

Blaise Pascal, qui aurait découvert ce théorème à seize ans, lui a donné le nom d'hexagramme mystique[1].

EulerHexagrammePascal.PNG

Sommaire

Cas particuliers

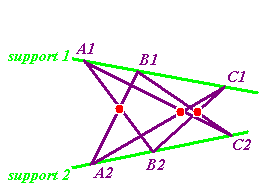
Si la conique est une bidroite, les droites forment deux supports recevant chacun trois points de l'hexagone. Il s'agit ici du théorème de Pappus.

Hexagramme2supports.PNG

Autres configurations

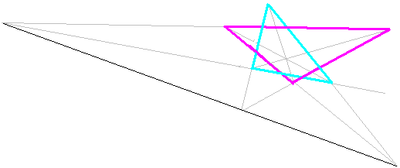
En utilisant une étoile de David irrégulière (deux triangles entrelacés), on peut retrouver les trois intersections alignées. Dans ce cas, ce n'est plus un hexagone, et l'alignement est expliqué par le théorème de Desargues.

EtoiledeDavidirreguliere.PNG

Notes

  1. ↑ Comme l'explique Leibniz dans les Notes de Leibniz et de Tschirnhaus sur les Coniques : « Hexagrammum pascallanum mysticum ut vocat idemque semper conicum. » (« Hexagramme de Pascal, mystique comme il l'appelle, et qui est toujours conique »)

Voir aussi

Liens externes


Articles de Géométrie projective ou voisins à consulter. [modifier]
Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes  • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques) 
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Hexagramme de Pascal ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hexagramme de pascal de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Hexagramme De Pascal — Pour les articles homonymes, voir Hexagramme. L hexagramme de Pascal, ou hexagramme mystique, est une figure géométrique illustrant le théorème de Pascal. Il représente un hexagone quelconque inscrit dans une conique. Ce théorème démontre que les …   Wikipédia en Français

  • Hexagramme de Pascal — Pour les articles homonymes, voir Hexagramme. L hexagramme de Pascal, ou hexagramme mystique, est une figure géométrique illustrant le théorème de Pascal. Il représente un hexagone quelconque inscrit dans une conique. Ce théorème démontre que les …   Wikipédia en Français

  • Hexagramme —  Ne doit pas être confondu avec Hexagramme de Pascal. Un hexagramme (六十四卦 liùshísì guà) est un symbole constitué de trait yīn et de trait yáng utilisé dans le Yì Jīng. Ils sont au nombre de soixante quatre et résultent de la combinaison de… …   Wikipédia en Français

  • hexagramme — (è gza gra m ) s. m. 1°   Terme didactique. Assemblage de six lettres ou caractères. 2°   Terme de mathématique. Hexagramme mystique, nom d un certain théorème de Pascal : si un hexagramme est inscrit dans une section conique, les points de… …   Dictionnaire de la Langue Française d'Émile Littré

  • Droite de Pascal — Théorème de Pascal Il existe plusieurs théorèmes appelés théorème de Pascal. Sommaire 1 Géométrie 1.1 Théorème de Pascal (direct et réciproque) 1.1.1 Théorème de Pappus Pascal …   Wikipédia en Français

  • Theoreme de Pascal — Théorème de Pascal Il existe plusieurs théorèmes appelés théorème de Pascal. Sommaire 1 Géométrie 1.1 Théorème de Pascal (direct et réciproque) 1.1.1 Théorème de Pappus Pascal …   Wikipédia en Français

  • Théorème de pascal — Il existe plusieurs théorèmes appelés théorème de Pascal. Sommaire 1 Géométrie 1.1 Théorème de Pascal (direct et réciproque) 1.1.1 Théorème de Pappus Pascal …   Wikipédia en Français

  • L'Hexagramme — est un ensemble de six romans écrits entre 1958 et 1970 par Jean Pierre Faye, à savoir: Entre les rues 1958, La Cassure 1961, Battement 1962, Analogues 1964, L Écluse 1964 et Les Troyens 1970. Lire L’Hexagramme ou de l’un à l’autre L Hexagramme… …   Wikipédia en Français

  • Théorème de Pascal — Il existe plusieurs théorèmes appelés théorème de Pascal. Sommaire 1 Géométrie 1.1 Théorème de Pascal (direct et réciproque) 1.1.1 Théorème de Pappus Pascal …   Wikipédia en Français

  • Blaise Pascal — Pour les articles homonymes, voir Pascal. Blaise Pascal Philosophe et Scientifique Époque Moderne …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”