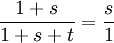- Heptagone régulier
-
Heptagone
Un heptagone est un polygone à sept sommets et sept côtés.
Un heptagone régulier est un heptagone dans lequel tous les côtés sont égaux et tous les angles sont égaux. Les angles sont alors tous égaux à
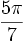 . L'heptagone régulier s'inscrit dans un cercle et les angles au centre associés à chacun de ses côtés sont tous égaux à
. L'heptagone régulier s'inscrit dans un cercle et les angles au centre associés à chacun de ses côtés sont tous égaux à 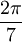 . Le rapport entre la longueur d'un côté et le rayon du cercle circonscrit est alors :
. Le rapport entre la longueur d'un côté et le rayon du cercle circonscrit est alors :L'aire A d'un heptagone régulier est déterminée par la formule suivante où c représente la longueur d'un côté :
L'heptagone régulier est le plus petit des polygônes réguliers non constructible à la règle et au compas car 7 est un nombre premier qui n'est pas de Fermat (théorème de Gauss-Wantzel) .
Il est cependant possible de réaliser une construction à la règle et au compas si on s'aide d'autres outils géométriques ou si la règle peut être graduée. Il est aussi possible d'en tracer une version approchée, aux erreurs faibles, avec le compas et la règle.
Sommaire
Non constructiblité
L'heptagone régulier n'est pas constructible car 7 n'est pas un nombre de Fermat. On peut aussi démontrer cette propriété de non-constructiblité sans faire appel au nombre de Fermat , en faisant seulement appel au théorème de Wantzel
Si l'heptagone était constructible alors
 serait un nombre constructible. Notons
serait un nombre constructible. Notons 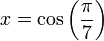 . Les angles
. Les angles 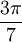 et
et 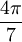 étant supplémentaires, on a l'égalité
étant supplémentaires, on a l'égalitéLes développements
- cos(4a) = 8cos4(a) − 8cos2(a) + 1
- cos(3a) = 4cos3(a) − 3cos(a)
transforment [1] en
- 8x4 − 8x2 + 1 = − 4x3 + 3x
Le passage de tout dans un membre et une factorisation par x + 1 conduit à
- (x + 1)(8x3 − 4x2 − 4x + 1) = 0
Le réel x est donc racine de 8x3 − 4x2 − 4x + 1 irréductible sur
 et de degré 3. Donc
et de degré 3. Donc  n'est pas constructible, par conséquent l'heptagone n'est pas constructible.
n'est pas constructible, par conséquent l'heptagone n'est pas constructible.Construction par neusis
Une construction par neusis ou par inclinaison est un procédé de construction utilisant une règle graduée et consistant à construire un segment de longueur donnée dont les extrémités se trouvent sur deux courbes données. Il s'agit ici de construire un angle de
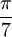 .
.Une construction préliminaire
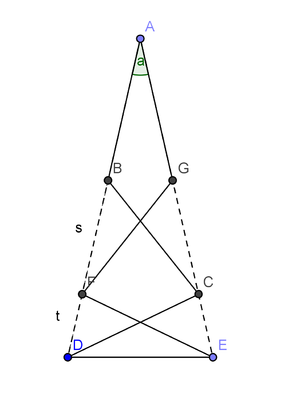
Dans la figure jointe, ABCDEFGA est un polygone où tous les segments sont de longueur 1. ABFD sont alignés et AGCE aussi.
L'angle DAE vaut
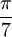
- Si on note cet angle a, alors le triangle ABC étant isocèle, l'angle CBD vaut 2a.
- Le triangle BCD étant isocèle, la somme des angles DCE et BCA vaut 4a, comme BCA vaut a, l'angle DCE vaut 3a
- Le triangle CDE étant isocèle, l'angle AED vaut 3a
- Le triangle ADE étant isocèle, la somme des angles vaut 7a donc
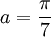
La longueur BE vaut
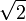
- On note s et t les longueurs BF et FD.
- Le triangle FDE étant isocèle, 2cos(EDF) = t
- Les droites (FC) et (DE) étant parallèles, l'angle ACF vaut 3a. Comme l'angle ACB vaut a, l'angle BCF vaut 3a-a = 2a. Le triangle BFC est donc isocèle et FC = FB = s
- Le même parallélisme permet de dire, d'après le théorème de Thales, que
- qui par produit en croix et simplification donne s2 + st = 1
- Le théorème d'Al-Kashi dans le triangle BDE donne alors
- BE2 = BD2 + DE2 − 2.BD.DE.cos(EDF) = 1 + (s + t)2 − t(s + t) = 1 + s2 + st = 2
La construction par neusis
Il s'agit de construire un point A sur la médiatrice d'un segment [DE] et un point B sur le segment [AD] tels que AB = 1 et BE =
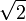 . On aura alors reconstitué le triangle précédent.
. On aura alors reconstitué le triangle précédent.- On construit un carré CDEF de côté 1, on trace la médiatrice (d) de [DE] et le cercle de centre E et de rayon EC
- On place l'origine de la règle sur la médiatrice, la règle s'appuie sur le point D, on fait glisser l'origine de la règle sur la médiatrice jusqu'à ce que le cercle (C) traverse la règle à la graduation 1. On obtient alors les point B et A
- On construit le cercle circonscrit aux points ADE qui se trouve être aussi le cercle circonscrit de l'heptagone de base DE qu'il suffit de construire.
Constructions approchées
À l'aide d'un triangle équilatéral
La recherche approchée de la solution de l'équation 8x3 − 4x2 − 4x + 1 = 0 comprise entre
 et 1 par la méthode de Newton donne pour valeur de x une valeur voisine de 0,901. En prenant comme valeur approchée de sin(π / 7), le réel
et 1 par la méthode de Newton donne pour valeur de x une valeur voisine de 0,901. En prenant comme valeur approchée de sin(π / 7), le réel 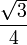 , on obtient pour une valeur approchée de
, on obtient pour une valeur approchée de  , la valeur
, la valeur 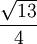 très voisine de 0,901. Or la longueur
très voisine de 0,901. Or la longueur 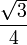 est très facile à obtenir à l'aide d'un triangle équilatéral.
est très facile à obtenir à l'aide d'un triangle équilatéral.
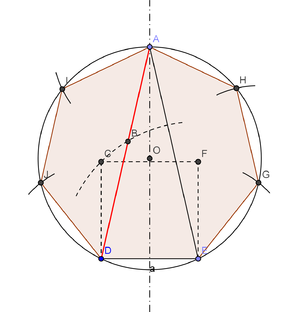
D'où la construction suivante :- Tracer un cercle de rayon 1 et de centre M.
- Prendre un point X sur le cercle. Le cercle de centre X et de rayon XM rencontre le cercle précédent en A et Y
- Les droites (AY) et (MX) se coupent en H.
- La longueur AH est une bonne approximation du côté de l'heptagone inscrit dans ce même cercle.
Par cette méthode l'angle au centre est d'environ 51,32 degrés au lieu des 51,43 (environ) attendu, soit une erreur relative de 2,15 pour mille
Construction à l'aide d'un découpage de segment
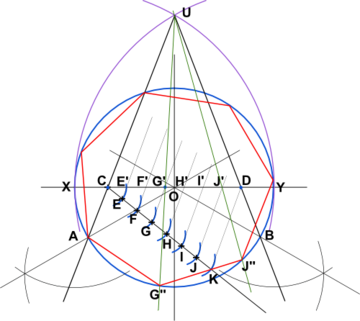
En s'inspirant de la construction de l'enneagone[1], on peut tracer une construction approchée d'un heptagone régulier, à la règle et au compas.
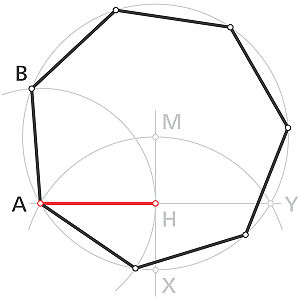
- Tracer le cercle de centre O de rayon OX
- Place, sur le cercle deux points A et B tels que l'angle AÔB = 120°.
- Tracer l'arc de cercle de rayon XY et de centre X
- Tracer l'arc de cercle de rayon YX et de centre Y
- Ces arcs se coupent en U
- Tracer les droites (UA) et (UB). Elles coupent le diamètre (XY) en C et D
- A partir de C, sur une droite quelconque, porter avec un compas sept segments égaux CE = EF = FG = GH = HI = IJ = JK
- Tracer la droite (KD) et mener par G une parallèle à celle-ci (au moyen de la règle et du compas), qui coupe (XY) en G’. Éventuellement tracer la parallèle à (KD) passant par J qui coupe (XY) en J’.
- Tracer la droite (UG').Elle coupe le cercle en G’’.
- Reportez au compas tout le long du cercle la longueur AG’’, on trouve alors les sept sommets de l'heptagone régulier inscrit dans le cercle.
Remarque : pour faire un heptagone comprenant le point B, il aurait fallu prendre les points H’’ ou E’’. De plus, en utilisant le point F’’, en reportant AF’’, on obtient un polygone à 21 sommets.
Par cette construction, l'angle au centre AOG’’est d'environ 51,327, soit une erreur relative de 1,98 pour mille équivalente à l'erreur obtenue par la méthode précédente.
Cette méthode permet de faire n'importe quel polygone régulier. Il suffit de sectionner le segment CD en autant de secteurs identiques qu'il y a de cotés souhaités pour le polygone. Ensuite, on prend le troisième point en partant de C (G’), on trace le segment qui le relie à U et on obtient G’’ à l'intersection entre le cercle et ce segment (dans le demi-plan inférieur à XY). L'erreur commise sur l'angle au centre pour cette méthode varie de 1,98 pour mille à 11,7 pour mille selon le nombre de côtés.
Heptagone régulier dans la vie courante
- La pièce de 20 centimes d'euros est découpée sous forme d'un heptagone régulier.
- Les pièces britanniques de 20 et de 50 pence sont également heptagonales.
Voir aussi
Notes
Liens internes
Lien externe
- [pdf] A propos de l'heptagone régulier et de sa construction, Baptiste Gorin
- Portail de la géométrie
Catégories : Polygone | Construction géométrique
Wikimedia Foundation. 2010.


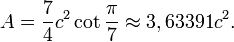
![\cos\left(\frac{4\pi}{7}\right)=-\cos\left(\frac{3\pi}{7}\right) \quad[1]](/pictures/frwiki/102/ff1f84b9578a92c5db7ba54a608b9b87.png)