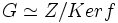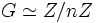Génération d'un groupe

Partie génératrice d'un groupe

En théorie des groupes, une partie génératrice d'un groupe G est une partie A telle que tout élément du groupe s'écrit comme produit d'un nombre fini d'éléments de A et de leurs inverses. L'ensemble G lui-même est une partie génératrice. En pratique, l'introduction d'une partie génératrice demande d'effectuer un choix judicieux pour l'utilisation qui en est faite.

Un groupe est dit de type fini lorsqu'il admet une partie génératrice finie.

Sommaire

1 Sous-groupe engendré par une partie
- 1.1 Exemple
2 Partie génératrice d'un groupe

Sous-groupe engendré par une partie

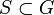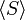L'intersection de sous-groupes de G est un sous-groupe de G. Pour une partie $S \subset G$ de $G$ , il existe un sous-groupe de $G$ , minimal pour l'inclusion, contenant $S$ , à savoir l'intersection de tous les sous-groupes contenant S. On l'appelle sous-groupe engendré par S, et noté $\left \langle S \right \rangle$ .

Description : Il est parfois utile de disposer d'une description explicite des éléments du groupe 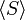$\left \langle S \right \rangle$ . Ce sont exactement les produits d'éléments ou d'inverses de $S$ :

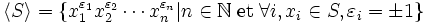$\left\langle S \right\rangle = \left\{ x_1^{\varepsilon _1} x_2^{\varepsilon _2} \cdots x_n^{\varepsilon _n} | n \in \mathbb{N} \; \mbox{et} \; \forall i, x_i \in S, \varepsilon_i = \pm 1 \right\}$ .

Si un groupe admet une partie génératrice finie, il est dit de type fini.

Exemple

Dans le groupe cyclique Z/ n Z, le sous-groupe engendré par la classe d'un entier k est le sous-groupe Z/ (n/d) Z où d désigne le PGCD de k et de n.

Dans le cas d'un groupe $G$ fini, l'inverse d'un élément $x$ est une puissance de $x$ (plus précisément, on a $x - 1 = x d - 1$ , où $d$ désigne l'ordre de $x$ ). Par suite, le sous-groupe engendré par un sous-ensemble $S$ d'un groupe fini $G$ , est l'ensemble des éléments de $G$ qui sont produits d'éléments de $S$ .

Partie génératrice d'un groupe

On dit que $S$ est une partie génératrice du groupe $G$ , ou que $G$ est engendré par $S$ lorsque le sous-groupe engendré par S est G :

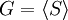$G = \langle S \rangle$ .

Autrement dit, tout élément de G est produit d'éléments de S ou de leurs inverses. Certaines fois, il peut être pratique de disposer d'un algorithme permettant d'expliciter un tel produit.

Groupe monogène

Article détaillé : groupe cyclique.

Le groupe $G$ est dit monogène s'il est engendré par un seul de ses éléments.

G

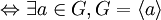
est monogène $\Leftrightarrow \exists a \in G, G = \langle a \rangle$

Si de plus $G$ est fini, alors on dit que $G$ est un groupe cyclique ou encore un cycle.

La classification des groupes monogènes n'est pas difficile. Si a engendre G, l'application 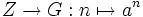$Z\rightarrow G:n\mapsto a^n$ est un homomorphisme de groupes. Par le théorème d'isomorphisme, cet homomorphisme induit l'isomorphisme :

$G\simeq Z/ Ker f$

Or, les sous-groupes de Z sont bien connus : il s'agit des groupes n Z avec 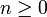$n\geq 0$ . De suite, l'isomorphisme ci-dessus s'écrit :

$G\simeq Z/nZ$

A isomorphisme près, il existe un unique groupe monogène infini, et pour chaque entier naturel n, un unique groupe cyclique de cardinal n.

Les générateurs de Z/n Z sont exactement les classes des entiers k premiers avec n. Leur cardinal est noté 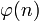$\varphi(n)$ . La fonction $\varphi$ est l'indicatrice d'Euler, elle joue un grand rôle en arithmétique.

Groupe abélien fini

Article détaillé : Théorème de Kronecker.

Un groupe abélien fini possède une structure simple, ce résultat est connu sous le nom de théorème de Kronecker : Soit G un groupe abélien fini :

Il existe une suite d'entiers strictement positifs (a₁,a₂,...,a_k) tel que G est isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite.

Il existe donc la suite suivante isomorphe au groupe G:

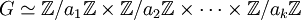
$G\simeq \mathbb{Z}/a_1\mathbb{Z}\times \mathbb{Z}/a_2\mathbb{Z} \times \cdots \times \mathbb{Z}/a_k\mathbb{Z}$

Groupe abélien de type fini

Article détaillé : groupe abélien de type fini.

Ce concept utilise la définition suivante :

Un groupe de type fini est un groupe possédant une partie génératrice finie.

Un groupe abélien de type fini ou groupe commutatif finiment engendré est un groupe abélien admettant une partie génératrice finie. A isomorphisme près, ces groupes sont des produits directs d'un nombre fini de groupes monogènes :

Si G est un groupe commutatif finiment engendré, il existe un unique entier r et une unique séquence finie 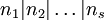$n_1|n_2|\dots|n_s$ telle qu'on dispose de l'isomorphisme :

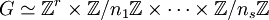$G\simeq \Z^r\times \Z/n_1\Z\times \dots\times \Z/n_s\Z$ .

Groupe linéaire

Le groupe SL_n(K) est engendré par les matrices de transvection.
Le groupe GL_n(K) est engendré par les matrices de transvection et une matrice de dilatation.

On dispose de l'algorithme de Gauss.

Portail des mathématiques

Ce document provient de « Partie g%C3%A9n%C3%A9ratrice d%27un groupe ».

Catégorie : Théorie des groupes

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Génération d'un groupe de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Groupe (mathématique) — Groupe (mathématiques) Pour les articles homonymes, voir Groupe. Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes … Wikipédia en Français
Groupe Sporadique — En mathématiques, un groupe sporadique est l un des 26 groupes exceptionnels dans la classification des groupes simples finis. Un groupe simple est un groupe G qui ne possède aucun sous groupe normal à part le sous groupe trivial réduit à l… … Wikipédia en Français
Generation de 27 — Génération de 27 La Génération de 27 ou Generación del 27 est un groupe littéraire qui apparut sur la scène espagnole entre les années 1923 et 1927, au sein duquel plusieurs poètes partagèrent des idées. Plusieurs se réunirent au domicile de… … Wikipédia en Français
Génération De 27 — La Génération de 27 ou Generación del 27 est un groupe littéraire qui apparut sur la scène espagnole entre les années 1923 et 1927, au sein duquel plusieurs poètes partagèrent des idées. Plusieurs se réunirent au domicile de Góngora, pour le… … Wikipédia en Français
Generation x (groupe) — Pour les articles homonymes, voir Generation X. Generation X est un groupe punk rock britannique fondé en 1976. À l origine, le groupe s appelait Chelsea et était composé de Billy Idol (guitare), Tony James (basse), John Towe (batterie) et Gene… … Wikipédia en Français
Generation — Génération Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Generation Swine — Album par Mötley Crüe Sortie 24 juin 1997 Enregistrement 1996 Durée 64:06 Genre Heavy metal Metal alternatif … Wikipédia en Français
Groupe De Bleau — Le « Groupe de Bleau » (ou « GdB » ou « Bleausards ») désigne le principal groupe de jeunes alpinistes parisiens qui, dans les années 1920 1930, allaient les dimanches faire de l escalade sur les rochers de forêt de… … Wikipédia en Français
Groupe de bleau — Le « Groupe de Bleau » (ou « GdB » ou « Bleausards ») désigne le principal groupe de jeunes alpinistes parisiens qui, dans les années 1920 1930, allaient les dimanches faire de l escalade sur les rochers de forêt de… … Wikipédia en Français
Groupe auxilaire de puissance — Groupe auxiliaire de puissance Pour les articles homonymes, voir APU. Le groupe auxiliaire de puissance (GAP), ou en anglais Auxiliary Power Unit (APU), désigne un groupe turbogénérateur auxiliaire destiné à produire de l énergie à bord des… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Génération d'un groupe

Partie génératrice d'un groupe

Sommaire