Groupe de fischer

Groupe de fischer

Groupe de Fischer

En mathématiques, le terme groupes de Fischer fait habituellement référence aux trois groupes finis notés Fi22, Fi23 et Fi24', tous sont des groupes simples et constituent trois des vingt-six groupes sporadiques. Quelquefois, le terme comprend les groupes d'automorphismes de ces groupes.

Sommaire

Les groupes 3-transposition

Les groupes de Fischer sont des groupes finis nommés en l'honneur du mathématicien Bernd Fischer, qui les découvrit en étudiant les groupes 3-transposition. Ceux-ci sont des groupes G avec les propriétés suivantes :

  • G est engendré par une classe de conjugaison d'éléments d'ordre 2, appelés les 'transpositions de Fischer'.
  • Le produit de deux transpositions quelconques est d'ordre 1, 2 ou 3.

L'exemple typique d'un groupe 3-transposition est un groupe symétrique, où les transpositions de Fischer sont véritablement des transpositions. Fischer pouvait classer les groupes 3-transposition qui satisfaisaient certaines conditions techniques supplémentaires. Les groupes qu'il trouva tombèrent dans plusieurs classes infinies (aussi bien que les groupes symétriques, certaines classes des groupes symplectiques et orthogonaux remplissaient ses conditions) avec une exception pour les trois groupes de Fischer. Ces groupes sont habituellement identifiés avec la notation 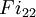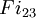Fi_{22}\,, Fi_{23}\, et Fi_{24}\,. 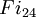Les deux premiers sont des groupes simples, et le troisième contient le groupe simple Fi24' d'index 2.

Ordres

L'ordre d'un groupe est le nombre d'éléments dans le groupe.

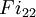Fi_{22}\, est d'ordre 217.39.52.7.11.13 = 64 561 751 654 400.

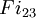Fi_{23}\, est d'ordre 218.313.52.7.11.13.17.23 = 4 089 470 473 293 004 800.

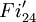Fi_{24}'\, est d'ordre 221.316.52.73.11.13.17.23.29 = 1 255 205 709 190 661 721 292 800. C'est le troisième plus grand groupe sporadique (après le groupe Monstre et le groupe Bébé Monstre).

Notation

Il n'existe malheureusement pas de notations uniformément acceptées pour ces groupes. Certains auteurs utilisent F à la place de Fi (e.g. 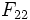F_{22}\,). La notation de Fischer pour eux était M(22), M(23) et M(24)', qui soulignait leur rapport étroit avec les trois plus grands groupes de Mathieu, 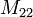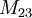M_{22}\,, M_{23}\, et M_{24}\,.

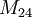Une source particulière de confusion réside dans le fait que 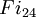Fi_{24}\, est quelquefois utilisé pour faire référence au groupe simple 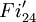Fi_{24}'\,, et est quelquefois utilisé pour faire référence au groupe 3-transposition entier (qui fait deux fois sa taille).

Références

  • 3-Transposition Groups (Cambridge Tracts in Mathematics) par Michael Aschbacher. "3-Transposition Groups" contient la première démonstration publiée du théorème de Fischer, écrite complètement en un endroit. Editeur : Cambridge University Press (28 novembre 1996) ISBN 0-521-57196-0
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe de Fischer ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe de fischer de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Groupe De Fischer — En mathématiques, le terme groupes de Fischer fait habituellement référence aux trois groupes finis notés Fi22, Fi23 et Fi24 , tous sont des groupes simples et constituent trois des vingt six groupes sporadiques. Quelquefois, le terme comprend… …   Wikipédia en Français

  • Groupe de Fischer — En mathématiques, les groupes de Fischer sont les trois groupes sporadiques Fi22, Fi23 et Fi24 . Quelquefois, le terme désigne les groupes d automorphismes de ces groupes. Sommaire 1 Les groupes 3 transposition 2 Ordres 3 …   Wikipédia en Français

  • Groupe Sporadique — En mathématiques, un groupe sporadique est l un des 26 groupes exceptionnels dans la classification des groupes simples finis. Un groupe simple est un groupe G qui ne possède aucun sous groupe normal à part le sous groupe trivial réduit à l… …   Wikipédia en Français

  • Groupe Monstre —  Pour l’article homonyme, voir Groupe monstre de Tarski (en).  En mathématiques, le Monstre M ou groupe de Fischer Griess F1 est le plus gros des 26 groupes simples …   Wikipédia en Français

  • Groupe sporadique — En mathématiques, un groupe sporadique est l un des 26 groupes exceptionnels dans la classification des groupes simples finis. Un groupe simple est un groupe G non trivial qui ne possède aucun sous groupe normal à part son sous groupe trivial… …   Wikipédia en Français

  • Fischer — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Fischer », sur le Wiktionnaire (dictionnaire universel) Fischer est le mot allemand équivalent au… …   Wikipédia en Français

  • FISCHER (R.) — Raymond FISCHER 1898 1988 Comptant parmi les rares architectes français à avoir rejoint dans les années 1920 les rangs de l’avant garde la plus radicale, Raymond Fischer fut à la fois un ardent polémiste et un artiste inspiré. La poursuite d’une… …   Encyclopédie Universelle

  • Fischer Brewery — at the south entrance of Schiltigheim. Fischer is a brewery in Schiltigheim, France. Contents 1 History …   Wikipedia

  • Groupe communiste, républicain, citoyen et des sénateurs du Parti de gauche — Le groupe communiste, républicain, citoyen et des sénateurs du Parti de gauche (CRC SPG) est un groupe parlementaire français, rassemblant au Sénat des membres du PCF et du PG. Il succède au groupe communiste républicain et citoyen (CRC), et… …   Wikipédia en Français

  • Groupe Alliance 90 / Les Verts au Bundestag — Groupe d Alliance 90 / Les Verts au Bundestag Salle de réunion du groupe d’Alliance 90 / Les Verts au palais du Reichstag, avec les parlementaires Grietje Bettin et Christian Simmert Le groupe d’Alliance 90 / Les Verts au Bundestag… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”