Théorème d'Engel

Théorème d'Engel

Théorème d'Engel

Le théorème d'Engel est un théorème portant sur la structure des algèbres de Lie. Sommairement, il affirme que les deux notions de nilpotence que l'on peut définir pour une algèbre de Lie coïncident.

Rappelons qu'une algèbre de Lie 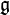\mathfrak{g} est dite nilpotente si la suite définie par récurrence par Ci par 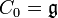C_0=\mathfrak{g} et C_{i+1}=[C_i,\mathfrak{g}] finit par arriver à 0, autrement dit s'il existe un i tel que Ci = {0}.

Rappelons également qu'un endomorphisme A d'un espace vectoriel V est dit nilpotent s'il existe un entier n tel que An = 0.

Si 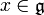x\in\mathfrak g, on note ad(x) l'endomorphisme de 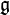\mathfrak g défini par ad(x)(y)=[x,y]. On dit que x est ad-nilpotent si ad(x) est nilpotent. Il découle facilement de la définition que si 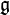\mathfrak g est une algèbre de Lie nilpotente, alors tout élément x de 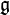\mathfrak g est ad-nilpotent.

Le théorème d'Engel s'énonce alors comme suit :

Théorème. Si tous les éléments d'une algèbre de Lie 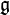\mathfrak g sont ad-nilpotents, alors 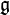\mathfrak g est nilpotente.

Ce théorème découle en fait du résultat suivant, que certains auteurs appellent également théorème d'Engel :

Théorème. Soit 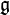\mathfrak g une sous-algèbre de Lie de 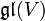\mathfrak {gl}(V). On suppose que tous les éléments de 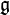\mathfrak g sont nilpotents. Alors il existe une base de V dans laquelle tous les éléments de 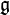\mathfrak g sont des matrices triangulaires supérieures (strictes).


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me d%27Engel ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème d'Engel de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Théorème de Engel — Le théorème de Engel porte sur la structure des algèbres de Lie. Sommairement, il affirme que les deux notions de nilpotence que l on peut définir pour une algèbre de Lie coïncident. Rappelons qu une algèbre de Lie est dite nilpotente si la suite …   Wikipédia en Français

  • Théorème de lie — Le théorème de Lie porte sur la structure des algèbres de Lie résolubles. Comme le théorème d Engel, il s agit d un théorème de réduction simultanée. Le théorème s énonce ainsi : Théorème : Soit un corps algébriquement clos de… …   Wikipédia en Français

  • Théorème de Lie — Le théorème de Lie porte sur la structure des algèbres de Lie résolubles. Comme le théorème d Engel, il s agit d un théorème de réduction simultanée. Le théorème s énonce ainsi : Théorème : Soit un corps algébriquement clos de… …   Wikipédia en Français

  • Friedrich Engel — Pour les articles homonymes, voir Friedrich Engels, Engel et Engels (homonymie). Friedrich Engel, né le 26 décembre 1861 à Lugau près de Chemnitz, mort le 29 septembre 1941 à Gießen, est un mathématicien allemand. Nommé à l université de Leipzig… …   Wikipédia en Français

  • Loi d'Engel — La loi d Engel est une loi empirique avancée en 1857 par le statisticien allemand Ernst Engel[1]. D après cette loi, la part du revenu allouée aux dépenses alimentaires (ou coefficient d Engel) est d autant plus faible que le revenu est élevé.… …   Wikipédia en Français

  • Loi de Engel — Loi d Engel La loi d Engel est une loi empirique avancée en 1857 par le statisticien allemand Ernst Engel[1]. D après cette loi, la part du revenu allouée aux dépenses alimentaires (ou coefficient d Engel) est d autant plus faible que le revenu… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”