Algorithme De Parcours En Profondeur

Algorithme De Parcours En Profondeur

Algorithme de parcours en profondeur

L'algorithme de parcours en profondeur (ou DFS, pour Depth First Search) est le principe qui s'abstrait de ce qu'on connait comme la façon simple de parcourir un labyrinthe sans tourner en rond. La pédagogie de l'informatique l'enseigne aujourd'hui volontiers en termes de parcours récursif d'un graphe quelconque.

Principe

C'est un algorithme de recherche qui progresse à partir d'un sommet S en s'appelant récursivement pour chaque sommet voisin de S.

Le nom d'algorithme en profondeur est dû au fait que, contrairement à l'algorithme de parcours en largeur, il explore en fait « à fond » les chemins un par un: pour chaque sommet, il prend le premier sommet voisin jusqu'à ce qu'un sommet n'ait plus de voisins (ou que tous ses voisins soient marqués), et revient alors au sommet père.

Si G n'est pas un arbre, l'algorithme pourrait tourner indéfiniment, c'est pour cela que l'on doit en outre marquer chaque sommet déjà parcouru, et ne parcourir que les sommets non encore marqués.

Enfin, on notera qu'il est tout à fait possible de l'implémenter itérativement à l'aide d'une pile LIFO contenant les sommets à explorer: on dépile un sommet et on empile ses voisins non encore explorés.

Implémentation récursive

DFS (graphe G, sommet s):
{
Marquer(S);
debut
POUR CHAQUE élément sfils de Voisin(s) FAIRE
   SI NonMarqué(sfils)
    ALORS DFS(G,sfils);
   FIN-SI
FIN-POUR
fin
}

Voisin(s) : renvoie la liste des sommets adjacents à s.

Marquer(Nœud ) : marque un nœud, de manière à ne pas le considérer plusieurs fois.

SousArbre(nœud u) : retourne le sous-arbre de racine u.

Exemple

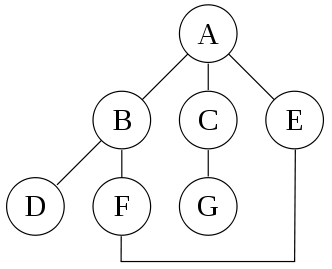
Voyons concrètement le fonctionnement de cet algorithme sur le graphe suivant:

Graph.traversal.example.svg

L'algorithme DFS commence au sommet A, nous conviendrons que les sommets à gauche sur ce graphe seront choisis avant ceux de droite. Si l'algorithme utilise effectivement un marquage des sommets pour éviter de tourner indéfiniment en boucle, on aura alors l'ordre de visite suivant: A, B, D, F, E, C, G.

Supposons maintenant que nous n'utilisions pas la méthode de marquage, on aurait alors la visite des sommets suivants dans l'ordre: A, B, D, F, E, A, B, D, F, E, etc indéfiniment, puisque l'algorithme ne peut sortir de la boucle A, B, D, F, E et n'atteindra donc jamais C ou G.

Ou encore:

Profondeur(G,s)
 Pour chaque u dans N faire
   vu[u] := faux
 rp(G,s)

rp(G,u)
 vu[u] := vrai
 pour chaque arete (u,v) dans A faire
    si vu[v] := faux alors
       rp(G,v)

G=(N,A), N étant les sommets et A les arêtes d'un graphe et s un sommet de depart.

vu est un tableau de booléen vu[i] := vrai si et seulement si le sommet est accessible de s.

Ce document provient de « Algorithme de parcours en profondeur ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algorithme De Parcours En Profondeur de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Algorithme de parcours en profondeur — L algorithme de parcours en profondeur (ou DFS, pour Depth First Search) est un algorithme de parcours de graphe qui se décrit naturellement de manière récursive. Son application la plus simple consiste à déterminer s il existe un chemin d un… …   Wikipédia en Français

  • Algorithme De Parcours En Largeur — Pour les articles homonymes, voir BFS. L algorithme de parcours en largeur (ou BFS, pour Breadth First Search) permet le parcours d un graphe de manière itérative, en utilisant une file. Il peut par exemple servir à déterminer la connexité d un… …   Wikipédia en Français

  • Algorithme de parcours en largeur — Pour les articles homonymes, voir BFS. L algorithme de parcours en largeur (ou BFS, pour Breadth First Search) permet le parcours d un graphe de manière itérative, en utilisant une file. Il peut par exemple servir à déterminer la connexité d un… …   Wikipédia en Français

  • Parcours (graphe) — Pour les articles homonymes, voir Parcours (homonymie).  Pour l’article homophone, voir parkour. En théorie des graphes, un parcours de sommets (resp. d arêtes, d arcs) dans un graphe G est une liste ordonnée de sommets (resp. d arêtes, d… …   Wikipédia en Français

  • Algorithme de Tarjan — En théorie des graphes, l algorithme de Tarjan permet de déterminer les composantes fortement connexes d un graphe orienté[1]. Il porte le nom de son inventeur, Robert Tarjan. L algorithme de Tarjan est de complexité linéaire, comme l algorithme… …   Wikipédia en Français

  • Algorithme de recherche en faisceau — En informatique, la recherche en faisceau est un algorithme de recherche heuristique qui explore un graphe en ne considérant qu un ensemble limité de fils de chaque nœud. La recherche en faisceau est une optimisation de l algorithme de parcours… …   Wikipédia en Français

  • Parcours de graphe —  Pour l’article homophone, voir parkour. En théorie des graphes, un parcours de graphe est un algorithme consistant à explorer les sommets d un graphe de proche en proche à partir d un sommet initial. Le mot parcours est également utilisé… …   Wikipédia en Français

  • Algorithme de Tremaux — Modélisation mathématique d un labyrinthe Une approche mathématique permet la génération de labyrinthes modernes. Les labyrinthes peuvent être modélisés dans un espace multi dimensionnel, les plus courants étant les labyrinthes en deux dimensions …   Wikipédia en Français

  • Algorithme de Trémaux — Modélisation mathématique d un labyrinthe Une approche mathématique permet la génération de labyrinthes modernes. Les labyrinthes peuvent être modélisés dans un espace multi dimensionnel, les plus courants étant les labyrinthes en deux dimensions …   Wikipédia en Français

  • Depth-first search — Algorithme de parcours en profondeur L algorithme de parcours en profondeur (ou DFS, pour Depth First Search) est le principe qui s abstrait de ce qu on connait comme la façon simple de parcourir un labyrinthe sans tourner en rond. La pédagogie… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”