- Graphe d'une fonction
-
Le graphe d'une fonction f dont l'ensemble de départ s'appelle E et l'ensemble d'arrivée F, est le sous-ensemble G de E × F formé par les couples d'éléments liés par la correspondance :
L'ensemble G est appelé graphe de f car il permet d'en donner une représentation graphique dans le cas usuel où E et F sont des sous-ensembles de l'ensemble des nombres réels : en effet, on peut alors parfois représenter E et F sur deux axes sécants, chaque couple de G peut alors être représenté par un point dans le plan, muni d'un repère défini par les deux axes. On parle aussi de courbe représentative de la fonction.
Si la correspondance est une fonction dont l'ensemble de départ est le carré cartésien R² (ou C) et F l'ensemble des réels, on peut parfois représenter E comme un plan. Dans ce cas, le graphe de la fonction est une surface gauche dans l'espace euclidien à 3 dimensions.
Il est possible alors de se ramener à une représentation plane en considérant des courbes de niveau, c'est-à-dire en dessinant dans le plan de départ une carte altimétrique du relief de la surface gauche.
Lorsque E et F sont des espaces topologiques, F étant séparé, et que l'application f est continue, alors le graphe G de f est une partie fermée de E × F.
Voir aussi
Articles connexes
- Correspondance et relation, pour une définition plus générale dans le cadre de la théorie des ensembles ;
- Étude de fonction ;
- Représentation graphique.
Liens externes
- FooPlot - Tracer des graphes pour des fonctions mathématiques en 2D et en 3D
Wikimedia Foundation. 2010.

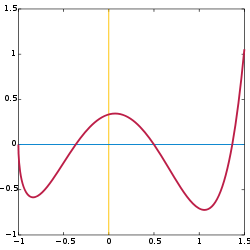
![\begin{align}&\scriptstyle f \colon [-1,1.5] \to [-1,1.5] \\ &\textstyle x \mapsto \frac{(4x^3-6x^2+1)\sqrt{x+1}}{3-x}\end{align}](e/55ecbb104124c17699f758a715f2b6a5.png)
