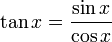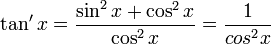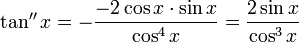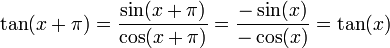Etude de fonction

Étude de fonction

Cet article concerne les fonctions réelles d'une seule variable.

L'étude d'une fonction ƒ est la détermination du comportement de la représentation graphique de cette fonction. La représentation graphique est l'ensemble des points du plan vérifiant

y = ƒ(x)

Par abus de langage, on parle parfois de graphe d'une fonction.

Sommaire

1 Méthode d'étude
2 Exemples
- 2.1 Exemple d'un polynôme
- 2.2 Exemple de la fonction tangente
3 Voir aussi
- 3.1 Articles connexes

Méthode d'étude

L'étude consiste à déterminer les points et directions particuliers et le comportement aux limites de l'intervalle de définition (qui peuvent être finis ou ±∞). Cela passe par le calcul de sa dérivée et de sa dérivée seconde :

discontinuité ;
sens de variation, défini par le signe de la dérivée ;
point d'inflexion ;
point de rebroussement ;
intersection avec les axes ;
tangente horizontale ;
asymptote.

Après avoir tracé et gradué les axes, on place les points particuliers, on trace les droites d'asymptote et les tangentes remarquables, puis à main levée, on trace une courbe lisse en passant par les point déterminés et respectant les directions.

On peut également calculer un certain nombre de points (par exemple une dizaine) judicieusement répartis pour faciliter le tracé. Ces points sont représentés sous la forme d'une croix droite (+).

Exemples

Exemple d'un polynôme

Représentation graphique de la fonction

Considérons le polynôme

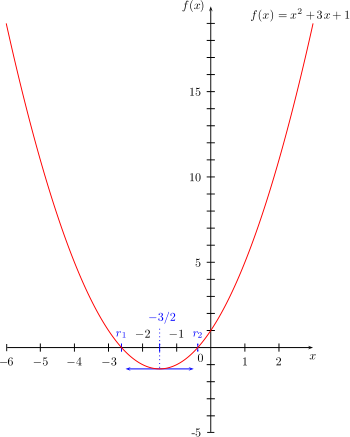
f(x) = x² + 3x + 1

On sait qu'il tend vers +∞ en +∞ et -∞ (f(x) ≈ x² en + et -∞) ;
il coupe l'axe des y en +1 (f(0) = 1) ;
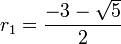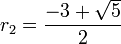
la résolution de l'équation du second degré nous indique qu'il coupe l'axe des x en $r_1=\dfrac{-3 - \sqrt{5}}{2}$ et en $r_2=\dfrac{-3 + \sqrt{5}}{2}$
sa dérivée vaut
f'(x) = 2x+3
elle s'annule en x = -3/2, il y a donc une tangente horizontale en ce point, la courbe est décroissante avant (f'<0), croissante après (f'>0) ;
sa dérivée seconde vaut
f''(x) = 2
la courbe est donc convexe, il n'y a pas de point d'inflexion

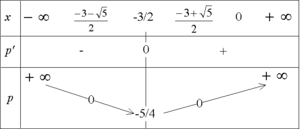
On a donc le tableau de variation suivant :

Tableau de variation sous forme d'image

On choisit un intervalle de x donnant des valeurs « représentables », un graphique lisible, par exemple [-6;3] ; sur cet intervalle, le polynôme va prendre des valeurs entre -1,25 (-5/4) et 19, on trace donc les axes. On place les points remarquables [-6;19], [-2,6;0] (première racine), (-1,5;-1,25) avec le bout de tangente horizontale, [-0.4;0] (deuxième racine), [0;1] et [3;19]. Puis, on trace la courbe à main levée.

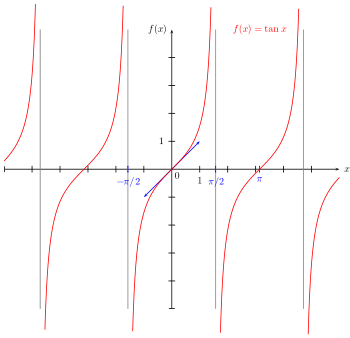
Exemple de la fonction tangente

La fonction tangente est définie par

$\tan{x}=\dfrac{\sin{x}}{\cos{x}}$

Les fonctions sinus et cosinus étant périodiques, c'est également une fonction périodique, il suffit donc de l'étudier sur un intervalle dont la largeur est la période. On ne connaît pas initialement la période de la tangente, on commence donc par prendre un intervalle de 2π, période du sinus et du cosinus ; prenons par exemple [-π, π].

Le cosinus s'annule pour des valeurs π/2 + k·π, et en ces valeurs, le sinus est non nul (il vaut ±1), donc en ces valeurs, la fonction tend vers ±∞.

Le sinus s'annule pour des valeurs k·π, et pour ces valeurs, le cosinus est non nul (il vaut ±1), donc la fonction s'annule pour ces valeurs.

Nous avons donc déterminé des asymptotes verticales π/2 + k·π, et des points de passage simples en k·π.

La dérivée vaut, d'après la loi de composition ((a/b)' = (a'b - ab' )/b²) :

$\tan' x = \dfrac{\sin^2 x + \cos^2 x }{\cos^2 x } = \dfrac{1}{cos^2 x }$

on voit donc que la fonction est toujours croissante, puisque sa dérivée est toujours positive, et que sa pente tend vers +∞ pour des valeurs de type π/2 + k·π, ce qui correspond aux asymtotes verticales.

La dérivée seconde vaut (avec 1/b' = -b'/b² et (c²)' = 2cc')

$\tan'' x = -\dfrac{-2\cos x \cdot \sin x }{\cos^4 x } = \dfrac{2 \sin x}{\cos^3 x}$

on voit que la dérivée seconde s'annule pour les valeurs k·π, il y a donc des points d'inflexion ; en ces points, la dérivée vaut 1.

On a donc le tableau de variation suivant :

Tableau de variation de p
x	-π		-π/2		0		π/2		π
tan'	1	+	+∞	+	1	+	+∞	+	1
tan	0	↗	+∞/-∞	↗	0	↗	+∞/-∞	↗	0

représentation graphique de la fonction tangente

Au vu de ce tableau, la fonction semble présenter une périodicité de π. On peut le vérifier simplement :

$\tan (x+\pi) = \dfrac{\sin(x+\pi)}{\cos(x+\pi)} = \dfrac{-\sin(x)}{-\cos(x)} = \tan(x)$

On peut donc restreindre l'intervalle de tracé à [-π/2;π/2]. On trace donc les asymptotes verticales x = π/2 + k·π, la tangente de pente 1 aux points d'inflexion (k·π, 0), puis on trace la fonction à main levée.

Voir aussi

Sur les autres projets Wikimedia :

Étude de fonction, sur Wikiversity (communauté pédagogique libre)

Regardez d'autres dictionnaires:

Étude de fonction — En mathématiques, une étude de fonction est la détermination de certaines propriétés d une fonction numérique, en général d une variable réelle, pour en tracer une représentation graphique à partir d une expression analytique ou d une… … Wikipédia en Français
Fonction de référence — En mathématiques, une fonction de référence est une fonction étudiée pour sa simplicité, son exemplarité ou afin de servir de support à l étude d une famille plus large de fonctions. Trois fonctions de référence Les fonctions de référence les… … Wikipédia en Français
Fonction (mathématique) — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Fonction Réelle — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Fonction et application — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Fonction mathématique — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Fonction réelle — Application (mathématiques) Pour les articles homonymes, voir Application. Graphique d une fonction … Wikipédia en Français
Fonction Entière — La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C … Wikipédia en Français
Fonction entiere — Fonction entière La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le … Wikipédia en Français
Fonction Zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Etude de fonction

Étude de fonction

Sommaire

Méthode d'étude