Graphe biparti
- Graphe biparti
-
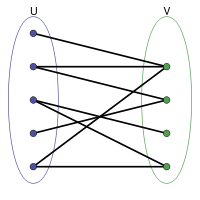
Exemple de graphe biparti quelconque
En théorie des graphes, un graphe est dit biparti s'il existe une partition de son ensemble de sommets en deux sous-ensembles U et V telle que chaque arête ait une extrémité dans U et l'autre dans V. En d'autres termes, les graphes bipartis sont précisément ceux dont le nombre chromatique est inférieur ou égal à 2.
Un graphe biparti permet notamment de représenter une relation binaire.
Il existe deux autres définitions équivalentes d'un graphe biparti. La première est purement graphique : Un graphe est biparti si et seulement s'il ne contient pas de cycle impair. La seconde est d'ordre polyédral : Un graphe est biparti si et seulement si son polytope des stables est décrit par les contraintes de clique de taille 2.
Un graphe biparti est dit biparti complet (ou encore est appelé une biclique) si chaque sommet de U est relié à chaque sommet de V.
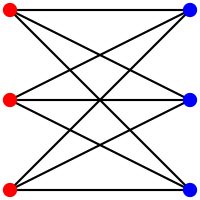
Exemple de graphe biparti complet
Catégories :
- Famille de graphes
- Concept en théorie des graphes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Graphe biparti de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Graphe Biparti — Exemple de graphe biparti quelconque En théorie des graphes, un graphe est dit biparti s il existe une partition de son ensemble de sommets en deux sous ensembles U et V telle que chaque arête ait une extrémité dans U et l autre da … Wikipédia en Français
Graphe biparti complet — K3,2 Notation Km,n Nombre de sommets m + n … Wikipédia en Français
Biparti — Graphe biparti Exemple de graphe biparti quelconque En théorie des graphes, un graphe est dit biparti s il existe une partition de son ensemble de sommets en deux sous ensembles U et V telle que chaque arête ait une extrémité dans U et l autre da … Wikipédia en Français
Graphe bipartite — Graphe biparti Exemple de graphe biparti quelconque En théorie des graphes, un graphe est dit biparti s il existe une partition de son ensemble de sommets en deux sous ensembles U et V telle que chaque arête ait une extrémité dans U et l autre da … Wikipédia en Français
Graphe Planaire — Dans la théorie des graphes, un graphe planaire est un graphe qui a la particularité de pouvoir se représenter sur un plan sans qu aucune arête (ou arc pour un graphe orienté) n en croise une autre. Autrement dit, ces graphes sont précisément… … Wikipédia en Français
Graphe hexaédrique — Représentation du graphe hexaédrique. Nombre de sommets 8 Nombre d arêtes 12 Distribution des degrés 3 régulier Rayon 3 … Wikipédia en Français
Graphe complet — K5 Notation Kn Nombre de sommets n Nombre d arêtes … Wikipédia en Français
Graphe Complet — K5 Notation Kn Nombre de sommets n Nombre d arêtes n(n − 1) / 2 … Wikipédia en Français
Graphe de Petersen — Schéma classique du graphe de Petersen, sous la forme d un pentagone et d un pentagramme concentriques, reliés par cinq rayons. Nombre de sommets 10 Nombre d arêtes 15 Distribution des degrés 3 régulier … Wikipédia en Français
Graphe de Desargues — Le graphe de Desargues Nombre de sommets 20 Nombre d arêtes 30 Distribution des degrés 3 régulier Rayon 5 … Wikipédia en Français


