- Graphe de Clebsch
-
Graphe de Clebsch 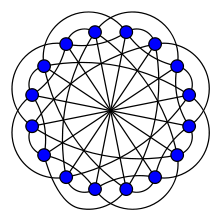
Représentation du graphe de ClebschNombre de sommets 16 Nombre d'arêtes 40 Distribution des degrés 5-régulier Rayon 2 Diamètre 2 Maille 4 Automorphismes 1 920 Nombre chromatique 4 Indice chromatique 5 Propriétés Fortement régulier
Hamiltonien
Cayleymodifier 
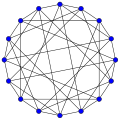
Le graphe de Clebsch est, en théorie des graphes, un graphe 5-régulier possédant 16 sommets et 40 arêtes.
Sommaire
Propriétés
Propriétés générales
Le graphe de Clebsch est un graphe fortement régulier de paramètres (v,k,λ,μ) = (16,5,0,2)[1],[2]. Son graphe complémentaire est également fortement régulier[3].
Le diamètre du graphe de Clebsch, l'excentricité maximale de ses sommets, est 2, son rayon, l'excentricité minimale de ses sommets, est 2 et sa maille, la longueur de son plus court cycle, est 4. Il s'agit d'un graphe 5-sommet-connexe et d'un graphe 5-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 5 sommets ou de 5 arêtes.
Le graphe de Clebsch est également un graphe non-planaire, un graphe non-eulérien et un hamiltonien.
Coloriage
Le nombre chromatique du graphe de Clebsch est 4. C'est-à-dire qu'il est possible de le colorer avec 4 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 3-coloration valide du graphe.
L'indice chromatique du graphe de Clebsch est 5. Il existe donc une 5-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le groupe d'automorphismes du graphe de Clebsch est d'ordre 1 920. Il est isomorphe au groupe de Coxeter D5. Ce groupe d'automorphismes agit transitivement sur l'ensemble des sommets du graphe de Clebsch, faisant de lui un graphe sommet-transitif[3].
Le polynôme caractéristique du graphe de Clebsch est : (x − 5)(x − 1)10(x + 3)5. Il n'admet que des racines entières. Le graphe de Clebsch est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers[3].
Galerie
-
Le graphe de Clebsch est hamiltonien.
-
Le nombre achromatique du graphe de Clebsch est 8.
-
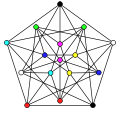
Le nombre chromatique du graphe de Clebsch est 4.
-
Construction du graphe de Clebsch depuis l'hypercube.
Voir aussi
Liens internes
Liens externes
- (en) Eric W. Weisstein, Clebsch Graph (MathWorld)
- (en) Andries E. Brouwer, Clebsch graph
Références
- C.D. Godsil, « Problems in algebraic combinatorics », dans Electron. J. Combin., vol. 2, 1995, p. 3 [texte intégral (page consultée le 2009-08-13)]
- Peter J. Cameron Strongly regular graphs on DesignTheory.org, 2001
- The Clebsch Graph on Bill Cherowitzo's home page
Catégorie :- Graphe remarquable
-
Wikimedia Foundation. 2010.