Formule de Mécanique des fluides

Formule de Mécanique des fluides

Formules de mécanique des fluides

Cet article fait partie de la série
formulaire de physique
Optique
Électro- Magnéstatique
Physique quantique
Thermodynamique
Mécanique des fluides
Mécanique
Relativité restreinte
Trou noir
Analyse vectorielle


Sommaire

Statique des fluides

Loi fondamentale de la statique des fluides

Pour un fluide au repos soumis à un champ de forces volumique 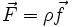\vec{F} = \rho \vec{f}, où ρ désigne la masse volumique, le champ de pression 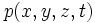\; p(x,y,z,t) vérifie la relation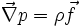

\vec{\nabla}p = \rho \vec{f}

Exemple: Lorsque le fluide est soumis uniquement aux forces de gravité 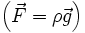\left( \vec{F} = \rho \vec{g} \right), on a la relation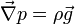

\vec{\nabla}p = \rho \vec{g}

soit, sachant que le champ de gravité est dirigé dans la direction verticale, (supposant le fluide incompressible ⇒ rho est constant )

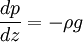
\frac{dp}{dz} = - \rho g

Poussée d'Archimède

Tout corps plongé dans un fluide est soumis à une poussée de bas en haut égale au poids du volume du fluide déplacé.

Soit un corps de masse volumique 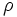\; \rho et de volume 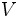\; V plongé dans un fluide de masse volumique ρf. La poussée d'Archimède que le fluide exerce sur ce corps est la force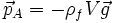

\vec{p}_A = - \rho_f V \vec{g}

Le poids apparent de ce corps dans le fluide est la somme de son poids et de la poussée d'Archimède, soit

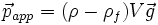
\vec{p}_{app} = (\rho - \rho_f) V \vec{g}

Remarque: Lorsque la masse volumique du corps est inférieure à celle du fluide, le poids apparent est négatif. Voilà pourquoi une planche de bois (masse volumique < 1) remonte à la surface de l'eau.

Dynamique des fluides parfaits incompressibles

Equations d'Euler pour un écoulement incompressible

Soit l'écoulement incompressible d'un fluide parfait, c'est-à-dire sans viscosité, dans un champ de force massique 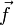\vec{f}. En première approximation, sa masse volumique 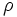\; \rho est constante. En un point quelconque du fluide 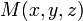\; M(x,y,z) et à un instant quelconque 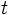\; t, les champs de pression 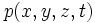\; p(x,y,z,t) et de vitesse 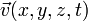\vec{v}(x,y,z,t) vérifient les relations: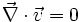

\vec{\nabla} \cdot \vec{v} = 0
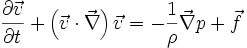
\frac{\partial \vec{v}}{\partial t} + \left( \vec{v} \cdot \vec{\nabla} \right) \vec{v} = - \frac{1}{\rho} \vec{\nabla} p + \vec{f}

En coordonnées cartésiennes 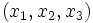\; (x_1, x_2, x_3), ces relations s'écrivent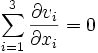

\sum_{i=1}^3 \frac{\partial v_i}{\partial x_i} = 0
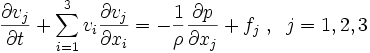
\frac{\partial v_j}{\partial t} + \sum_{i=1}^3 v_i \frac{\partial v_j}{\partial x_i} = - \frac{1}{\rho} \frac{\partial p}{\partial x_j} + f_j \; , \; \; j = 1,2,3

Ecoulement potentiel - Potentiel des vitesses

Un écoulement de fluide selon les normes de température et de pression est dit potentiel lorsque

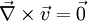
\vec{\nabla} \times \vec{v} = \vec{0}

Dans ce cas, il existe une fonction potentiel des vitesses 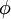\; \phi qui vérifie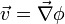

\vec{v} = \vec{\nabla} \phi

Relations de Bernoulli

Ecoulement stationnaire et potentiel

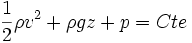
\frac{1}{2}\rho v^2 + \rho g z + p = Cte

en tout point de l'ecoulement.

Ecoulement stationnaire et non-potentiel

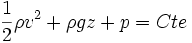
\frac{1}{2}\rho v^2 + \rho g z + p = Cte

le long d'une ligne de courant.

Ecoulement instationnaire et potentiel

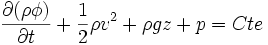
\frac{\partial (\rho \phi)}{\partial t} + \frac{1}{2}\rho v^2 + \rho g z + p = Cte

en tout point de l'ecoulement.

Dynamique des fluides visqueux incompressibles

Equations de Navier-Stokes pour un écoulement incompressible

Soit un écoulement incompressible de fluide visqueux dans un champ de force massique 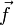\vec{f}. La viscosité cinématique du fluide est notée ν (unité SI: m2 / s). En un point quelconque du fluide 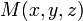\; M(x,y,z) et à un instant quelconque 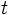\; t, les champs de pression 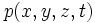\; p(x,y,z,t) et de vitesse 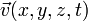\vec{v}(x,y,z,t) vérifient les relations: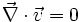

\vec{\nabla} \cdot \vec{v} = 0
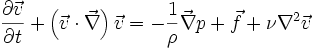
\frac{\partial \vec{v}}{\partial t} + \left( \vec{v} \cdot \vec{\nabla} \right) \vec{v} = - \frac{1}{\rho} \vec{\nabla} p + \vec{f} + \nu \nabla^2 \vec{v}

En coordonnées cartésiennes 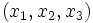\; (x_1, x_2, x_3), ces relations s'écrivent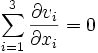

\sum_{i=1}^3 \frac{\partial v_i}{\partial x_i} = 0
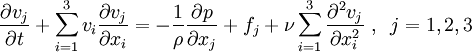
\frac{\partial v_j}{\partial t} + \sum_{i=1}^3 v_i \frac{\partial v_j}{\partial x_i} = - \frac{1}{\rho} \frac{\partial p}{\partial x_j} + f_j + \nu \sum_{i=1}^3 \frac{\partial^2 v_j}{\partial x_i^2}\; , \; \; j = 1,2,3

Articles connexes

  • Portail de la physique Portail de la physique
Ce document provient de « Formules de m%C3%A9canique des fluides ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule de Mécanique des fluides de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Portance (mécanique des fluides) — « Portance » redirige ici. Pour les autres significations, voir Portance (homonymie). La portance est la composante de la force subie par un corps en mouvement dans un fluide qui s exerce perpendiculairement à la direction du mouvement …   Wikipédia en Français

  • FLUIDES (MÉCANIQUE DES) — La mécanique des fluides constitue l’extension de la mécanique rationnelle à une classe de milieux continus dont les déformations peuvent prendre des valeurs aussi grandes que l’on veut. On désigne sous le nom général de fluides des corps… …   Encyclopédie Universelle

  • Mecanique des milieux continus — Mécanique des milieux continus La mécanique des milieux continus est le domaine de la mécanique qui s intéresse à la déformation des solides et à l écoulement des fluides ce dernier point fait l objet de l article mécanique des fluides, nous nous …   Wikipédia en Français

  • Mécanique Des Milieux Continus — La mécanique des milieux continus est le domaine de la mécanique qui s intéresse à la déformation des solides et à l écoulement des fluides ce dernier point fait l objet de l article mécanique des fluides, nous nous intéresserons donc ici… …   Wikipédia en Français

  • Mécanique des milieux continus — La mécanique des milieux continus est le domaine de la mécanique qui s intéresse à la déformation des solides et à l écoulement des fluides ce dernier point fait l objet de l article mécanique des fluides, nous nous intéresserons donc ici… …   Wikipédia en Français

  • Equations fondamentales de la mecanique des milieux continus — Équations fondamentales de la mécanique des milieux continus Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus,… …   Wikipédia en Français

  • Géophysique interne (équations fondamentales de la mécanique des milieux continus) — Équations fondamentales de la mécanique des milieux continus Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus,… …   Wikipédia en Français

  • Équations fondamentales de la mécanique des milieux continus — Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus, principalement applicables à la déformation des solides et à la …   Wikipédia en Français

  • Équations fondamentales de la mécanique des milieux continus) — Équations fondamentales de la mécanique des milieux continus Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus,… …   Wikipédia en Français

  • CINÉTIQUE DES FLUIDES (THÉORIE) — La théorie cinétique des fluides appartient à une branche de la physique qui se propose d’expliquer les propriétés macroscopiques des fluides à partir d’une analyse statistique des mouvements des particules qui les constituent. On peut classer… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”