Equations fondamentales de la mecanique des milieux continus

Equations fondamentales de la mecanique des milieux continus: Équations fondamentales de la mécanique des milieux continus

Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus, principalement applicables à la déformation des solides et à la mécanique des fluides.

Sommaire

1 Quelques quantités physiques intégrales du système

2 Lois de conservation

2.1 Conservation de la masse, ou équation de continuité

2.2 Conservation de l'impulsion, ou équation de mouvement

2.3 Conservation du moment cinétique, ou équation de rotation

2.4 Symétrie du tenseur des contraintes

2.5 Conservation de l'énergie

2.6 Tableau récapitulatif des principales lois de conservation

3 Hypothèses et lois pour décrire les déformations de la Terre

4 Loi de Hooke

5 Conditions aux frontières

5.1 Conditions cinématiques

5.2 Conditions dynamiques

6 Notes

7 Voir aussi

7.1 Bibliographie

7.2 Liens internes

7.3 Liens externes

Quelques quantités physiques intégrales du système

En général, on étudie les déformations et la dynamique de la Terre en termes d'un modèle de continuum caractérisé par une distribution interne de masse non spécifiée pour le moment, autrement dit par une densité^[1] massique $ρ$ , dans un volume $B$ délimité par une surface 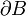$\partial B$ . Dans le problème qui nous occupe, cette frontière 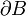$\partial B$ n'est pas donnée a priori, mais doit être déterminée en supposant qu'elle correspond à la forme d'équilibre du corps déformable. En outre, nous supposerons pour le moment qu'il existe un champ de vitesse $v i$ par rapport au système de référence choisi mais non encore spécifié, ainsi qu'une densité de moment cinétique interne 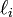$\ell_i$ , une force volumique $f i$ , un champ de contraintes (ou champ de tensions) $T i j$ , un moment de force volumique $M i$ et moment de force surfacique $M i j$ . Toutes ces quantités peuvent être des fonctions explicites ou implicites du temps $t$ . Sauf indication différente, nous utiliserons un système de référence cartésien dont l'origine (0, 0, 0) se trouve au point O. Nous dénoterons les coordonnées spatiales par $x i$ et les dérivées spatiales successives 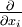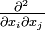$\tfrac{\par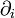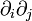tial}{\partial x_i}$ , $\tfrac{\partial^2}{\partial x_i \partial x_j}$ , ... par $\partial_i$ , $\partial_i \partial_j$ , ... (avec $i, j = 1,2,3$ ). En règle générale, nous adoptons ici la notation indicielle pour les vecteurs et les tenseurs, ainsi que la règle de sommation d'Einstein sur les indices muets répétés.

La masse totale du modèle est
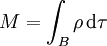
$M = \int_B \rho\,\mathrm d\tau$
où $dτ = d x 1 d x 2 d x 3$ est un élément de volume.

L'impulsion totale est
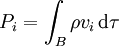
$P_i = \int_B \rho v_i\,\mathrm d\tau$
et le moment cinétique total est
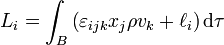
$L_i = \int_B \left(\varepsilon_{ijk} x_j \rho v_k + \ell_i \right) \mathrm d\tau$
où 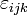$\varepsilon_{ijk}$ est le symbole de Levi-Civita.

La résultante des forces appliquée au volume $B$ du corps est
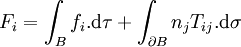
$F_i = \int_B f_i. \mathrm d\tau + \int_{\partial B}n_j T_{ij}. \mathrm d\sigma$
où $dσ$ est un élément de la surface 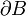$\partial B$ et $(n 1, n 2, n 3)$ dénote un vecteur unitaire normal à la surface 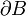$\partial B$ et pointant hors du volume $B$ . De la même, manière, le moment de force résultant appliqué au corps $B$ est
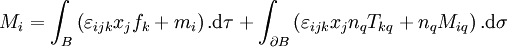$M_i = \int_B \left(\varepsilon_{ijk} x_j f_k + m_i \right). \mathrm d\tau + \int_{\partial B} \left(\varepsilon_{ijk} x_j n_q T_{kq} + n_q M_{iq} \right). \mathrm d\sigma$ .
Ces formules sont valables en toute circonstance. Si nous admettons en outre que la surface-frontière 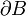$\partial B$ de $B$ est régulière et que les champs des tensions et des moments de force surfaciques sont différentiables dans $B$ , on peut appliquer le théorème de la divergence de Gauss et écrire :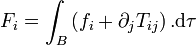
$F_i = \int_B \left(f_i + \partial_j T_{ij} \right). \mathrm d\tau$
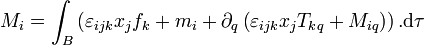$M_i = \int_B \left(\varepsilon_{ijk} x_j f_k + m_i + \partial_q \left(\varepsilon_{ijk} x_j T_{kq} + M_{iq} \right) \right). \mathrm d\tau$ .
Lois de conservation

Les équations régissant un milieu continu peuvent être déduites, soit en utilisant un « principe de correspondance » pour adapter les lois de la mécanique des points discrets de Newton aux points matériels de la mécanique des milieux continus,^[2] soit en exprimant de façon directe le fait que certains attributs physiques, tels que la masse, l'impulsion, le moment cinétique, l'énergie cinétique, l'énergie interne, l'énergie totale, etc., contenus dans un volume arbitraire $b (t)$ se déformant au cours du temps t, ne peuvent pas changer de manière arbitraire, mais que leurs changements précis sont régis par des lois de conservation. Ces dernières peuvent s'obtenir en exprimant le taux de changement dans le temps dans un volume arbitraire de matière au moyen du théorème de transport de Reynolds.

Soit $b (t)$ une partie quelconque se déformant au cours du temps du volume matériel $B (t)$ . On suppose que sa frontière 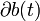$\partial b(t)$ est régulière, et on oriente la normale unitaire $n (t)$ en un point quelconque de 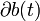$\partial b(t)$ vers l'extérieur. Pour une quantité physique arbitraire $q$ associée à un point matériel appartenant au volume $b (t)$ ou à sa frontière 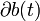$\partial b(t)$ , on a alors
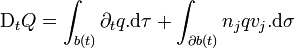$\mathrm D_t Q = \int_{b(t)} \partial_t q. \mathrm d\tau + \int_{\partial b(t)} n_j qv_j. \mathrm d\sigma$ .
Les notations utilisées ici sont les suivantes : 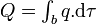$Q = \textstyle\int_b q. \mathrm d\tau$ est une quantité physique arbitraire, et $q$ la densité volumique du champ correspondant ; les opérateurs $D t$ et 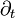$\partial_t$ sont les dérivations totales (matérielles) 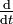$\tfrac{\mathrm d}{\mathrm dt}$ et partielles (locales) 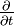$\tfrac{\partial}{\partial t}$ par rapport au temps, respectivement ; 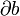$\partial b$ est la surface régulière fermée qui limite le volume $b$ , de normale extérieure unitaire $n i (i = 1,2,3)$ . En utilisant à nouveau le théorème de la divergence de Gauss, il vient
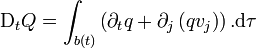$\mathrm D_t Q = \int_{b(t)} \left(\partial_t q + \partial_j \left(qv_j \right) \right). \mathrm d\tau$ .
Si $κ$ est le taux local de production ou de destruction de la quantité $Q$ , c'est-à-dire 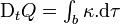$\mathrm D_t Q = \textstyle\int_b \kappa. \mathrm d\tau$ , alors la formule précédente devient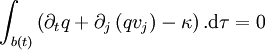
$\int_{b(t)} \left(\partial_t q + \partial_j \left(qv_j \right) - \kappa \right). \mathrm d\tau = 0$
ou, puisque le volume $b (t)$ est arbitraire et peut donc être pris arbitrairement petit :
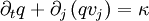$\partial_t q + \partial_j \left(qv_j \right) = \kappa$ .
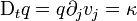Ceci est la forme eulérienne générale d'une loi de conservation en physique des milieux continus. La forme lagrangienne équivalente, valable pour chaque point matériel individuel, est $\mathrm D_t q = q \partial_j v_j = \kappa$ .

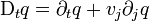On déduit cette forme lagrangienne aisément de la forme eulérienne à l'aide de l'identité (voir l'article Concepts de base en théorie des milieux continus) $\mathrm D_t q = \partial_t q + v_j \partial_j q$ .

Conservation de la masse, ou équation de continuité

Sous forme intégrale, la conservation de la masse s'exprime par^[3]
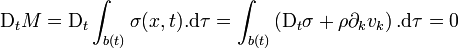$\mathrm D_t M = \mathrm D_t \int_{b(t)} \sigma (x,t). \mathrm d\tau = \int_{b(t)}\left(\mathrm D_t \sigma + \rho \partial_k v_k \right). \mathrm d\tau = 0$ .
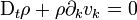Cette formule fournit l'équation de continuité, exprimant la conservation de la masse sous forme différentielle, en faisant tendre le volume arbitraire $b (t)$ tendre vers un point : $\mathrm D_t \rho + \rho \partial_k v_k = 0$ .

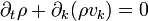La forme eulérienne de cette dernière équation est $\partial_t \rho + \partial_k(\rho v_k) = 0$ .

On remarque qu'il s'agit bien ici d'une forme particulière de la loi de conservation générale 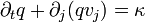$\partial_t q + \partial_j(qv_j) = \kappa$ , où $q = ρ$ et $κ = 0$ . Le fait que $κ = 0$ indique bien qu'il n'y a ni production ni destruction de masse, laquelle est donc conservée.

Conservation de l'impulsion, ou équation de mouvement

De manière similaire, à peine plus compliquée, on peut établir l'équation de conservation de l'impulsion régissant le mouvement d'un point matériel, en posant $q = ρ v i$ et en admettant explicitement que la masse se conserve aussi. On obtient
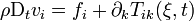$\rho \mathrm D_t v_i = f_i + \partial_k T_{ik}(\xi ,t)$ .
En effet, l'équation fondamentale de la dynamique exprime le fait que le taux de variation de l'impulsion $D t P i$ est équilibré par la résultante des forces $F i$ agissant sur le volume. On a donc
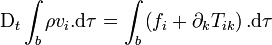$\mathrm D_t \int_b \rho v_i. \mathrm d\tau = \int_b \left(f_i + \partial_k T_{ik} \right). \mathrm d\tau$ .
Si nous transformons le membre de gauche au moyen du théorème de Reynolds, nous obtenons
$\mathrm D_t \int_{b(t)} \left[\partial_t \left(\rho v_i \right) + \partial_k \left(\rho v_i v_k \right) \right]. \mathrm d\tau = \int_{b(t)} \left(f_i + \partial_k T_{ik} \right). \mathrm d\tau$ .
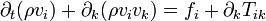Dès lors, en faisant tendre le volume arbitraire $b$ vers zéro, on obtient la forme eulérienne générale de l'équation de mouvement, à savoir $\partial_t( \rho v_i ) + \partial_k ( \rho v_i v_k ) = f_i + \partial_k T_{ik}$ .

Il convient de noter que dans cette équation, on ne présuppose aucunément qu'il y ait conservation de masse, mais seulement que le tenseur des contraintes $T i k$ est différentiable. En développant le membre de gauche, on obtient
$\rho \left[ \partial_t v_i + v_k \partial_k v_i \right] + v_i \left[ \partial_t \rho + \partial_k \left( \rho v_k \right) \right] = f_i + \partial_k T_{ik}$ .
Le terme entre crochets dans le membre de gauche représente l'accélération $D t v i$ . Le terme entre accolades dans ce même membre de gauche représente simplement l'équation de conservation de la masse sous forme eulérienne. 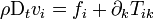Ainsi donc, si nous supposons que la masse reste conservée — ce qui est pratiquement toujours le cas en géophysique interne — l'équation de conservation de la quantité de mouvement s'écrit $\rho \mathrm D_t v_i = f_i + \partial_k T_{ik}$ .

Conservation du moment cinétique, ou équation de rotation

L'équation exprimant la conservation du moment cinétique, qui est primordiale dans les études traitant de la rotation d'un corps déformable comme la Terre, peut être obtenue de manière semblable à celle exprimant la conservation de l'impulsion. En supposant qu'il y ait conservation de la masse et conservation de la quantité de mouvement, on obtient
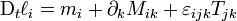$\mathrm D_t \ell_i = m_i + \partial_k M_{ik} + \varepsilon_{ijk} T_{jk}$ .
En effet, le taux de variation du moment cinétique $D t L i$ dans un volume arbitraire $b$ est équilibré par le moment de force résultant $M i$ agissant sur ce volume. Nous avons donc
$\mathrm D_t \int_b \left( \varepsilon_{ijk} x_j \rho v_k + \ell_i \right). \mathrm d\tau = \int_b \left[ \varepsilon_{ijk} x_j f_k + m_i + \partial_q \left( \varepsilon_{ijk} x_j T_{kq} + M_{iq} \right) \right] \mathrm d\tau$ .
Comme précédemment, on transforme le membre de gauche en appliquant le théorème de Reynolds pour obtenir
$\int_b \left[ \partial_t \left( \varepsilon_{ijk} x_j \rho v_k + \ell_i \right) + \partial_q \left( \rho \varepsilon_{ijk} x_j v_k v_q + \ell_i v_q \right) \right]. \mathrm d\tau = \int_b \left[ \varepsilon_{ijk} x_j f_k + m_i + \partial_q \left( \varepsilon_{ijk} x_j T_{kq} + M_{iq} \right) \right]. \mathrm d\tau$ .
En faisant tendre le volume arbitraire $b$ vers zéro, on obtient l'équation exprimant localement la conservation du moment cinétique, à savoir
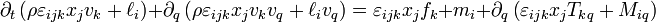$\partial_t \left( \rho \varepsilon_{ijk} x_j v_k + \ell_i \right) + \partial_q \left( \rho \varepsilon_{ijk} x_j v_k v_q + \ell_i v_q \right) = \varepsilon_{ijk} x_j f_k + m_i + \partial_q \left( \varepsilon_{ijk} x_j T_{kq} + M_{iq} \right)$ .
Cette équation peut être réarrangée comme suit :
$\langle\partial_t \ell_i + v_q \partial_q \ell_i\rangle + \varepsilon_{ijk} x_j v_k \left[ \partial_t \rho + \partial_q \left( \rho v_k \right) \right] + \varepsilon_{ijk} x_j \{ \rho \partial_t v_k + \rho v_q \partial_q v_k - f_k - \partial_q T_{kq} \} = m_i + \partial_q M_{iq} + \varepsilon_{ijk} \left( T_{kj}-\rho v_j v_k \right)$ .
Dans le membre de gauche, les termes entre chevrons représentent la quantité 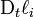$\mathrm D_t \ell_i$ , les termes entre crochets s'annulent si la masse est conservée, et les termes entre accolades s'annulent si à la fois la masse et l'impulsion sont conservées. Dans le membre à droite du signe =, le terme 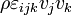$\rho \varepsilon_{ijk} v_j v_k$ est identiquement nul, puisque $v j v k$ est un tenseur symétrique. 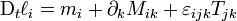Admettant que masse et impulsion soient conservées, on obtient donc $\mathrm D_t \ell_i = m_i + \partial_k M_{ik} + \varepsilon_{ijk} T_{jk}$ .

Symétrie du tenseur des contraintes

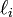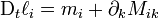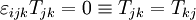Si, en outre, nous supposons que le moment cinétique intrinsèque $\ell_i$ d'un point matériel quelconque ne change pas au cours du mouvement de déformation, autrement dit si $\mathrm D_t \ell_i = m_i + \partial_k M_{ik}$ , alors le tenseur des contraintes $T j k$ est symétrique : $\varepsilon_{ijk} T_{jk} = 0 \equiv T_{jk} = T_{kj}$ .

Conservation de l'énergie

L'équation exprimant la conservation de l'énergie peut s'obtenir par la même méthode que celle employée pour la masse, la quantité de mouvement et la quantité de rotation. On trouve :
$\partial_t \left( \rho v^2 + U \right) + \partial_j \left[ \left( \frac{1}{2} \rho v^2 + U \right) v_j - v_k T_{kj} + H_j \right] = v_k f_k + \Gamma$ .
Le symbole $U$ désigne ici l'énergie interne par unité de volume, $H i$ est le vecteur densité de flux de chaleur, et $Γ$ est le taux de production ou de destruction intrinsèque d'énergie par unité de volume, par réactions chimiques, par radioactivité, ou par tout autre processus interne. Le symbole $v 2$ représente bien sûr le carré $v k v k$ de la vitesse, c'est-à-dire deux fois l'énergie cinétique par unité de masse.

Tableau récapitulatif des principales lois de conservation

Le tableau ci-dessous résume les principales lois de conservation générales, sous forme eulérienne, utiles pour résoudre les problèmes posés par la mécanique des milieux continus, en particulier lorsqu'il s'agit d'étudier les déformations globales de la Terre suite à un séisme, suite à une variation de la longueur du jour, suite à l'application d'un potentiel de marée ou suite à l'application d'une distribution de masse sur la surface externe. Les notations employées dans le tableau sont celles de ce texte. Rappelons que l'intégrale 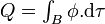$\textstyle Q = \int_B \phi. \mathrm d\tau$ est la quantité physique qui se conserve ; elle représente, selon les cas, la masse totale du corps $B$ , sa quantité de mouvement totale $P i$ , son moment cinétique total $L i$ , ou son énergie totale $E$ . 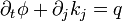La forme eulérienne générale d'une loi de conservation est $\partial_t \phi + \partial_j k_j = q$ .

Principales lois de conservation de la mécanique des milieux continus
$Q$ $φ$ $k j$ $q$

$M$ $ρ$ $ρ v j$ 0

$P i$ $ρ v i$ $ρ v i v j - T i j$ $f i$

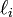
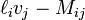
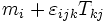
$L i$ $\e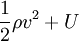ll_i$ $\ell_i v_j - M_{ij}$ $m_i + \varepsilon_{ijk} T_{kj}$

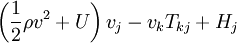
$E$ $\frac{1}{2} \rho v^2 + U$ $\left( \frac{1}{2} \rho v^2 + U \right) v_j - v_k T_{kj} + H_j$ $v k f k + Γ$

Hypothèses et lois pour décrire les déformations de la Terre

Article connexe : Lois de déformation.

Dans les problèmes de géodynamique théorique, on considère en général que la résultante des forces externes par unité de volume $f i$ se compose d'une force gravifique volumique 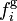$f_i^\text{g}$ causée par l'autogravitation et par l'attraction gravifique de corps extérieurs, d'une force électromagnétique volumique 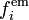$f_i^\text{em}$ , de forces volumiques inertielles (Coriolis et axifuge) 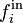$f_i^\text{in}$ , de forces de marée 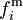$f_i^\text{m}$ , et de forces volumiques causées par des charges extérieures 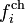$f_i^\text{ch}$ . D'autre part, les forces surfaciques $T i (x, t, n)$ dépendant de l'orientation $n$ qui contribuent en général au tenseur des contraintes $T i j (x, t)$ via les relations de Cauchy $T i (x, t, n) = T i j (x, t) n j (x, t, n)$ sont les forces élastiques qui engendrent un tenseur des contraintes élastiques 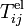$T_{ij}^\text{el}$ , les forces superficielles électromagnétiques qui engendrent un tenseur de Maxwell 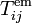$T_{ij}^\text{em}$ , des forces visqueuses qui engendrent un tenseur de Reynolds un tenseur des contraintes élastiques 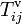$T_{ij}^\text{v}$ , des forces de frottement de contact non visqueux qui engendrent un tenseur des forces de friction un tenseur des contraintes élastiques 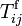$T_{ij}^\text{f}$ , et de toute autre force surfacique engendrant un tenseur des contraintes un tenseur des contraintes élastiques $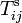T_{ij}^\text{s}$ .

La force de gravité par unité de masse $g$ , plus simplement appelée accélération gravifique ou gravité, dérive d'un potentiel gravifique $φ g$ que nous assimilerons ici à l'énergie potentielle gravifique^[4] :
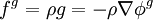$f^g = \rho g = - \rho \nabla \phi^g$ .
Le potentiel $φ g$ est déterminé par l'équation de Poisson
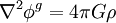$\nabla^2 \phi^g = 4 \pi G \rho$ ,
où $G$ est la constante de gravitation. Il convient de noter que les propriétés du potentiel gravifique impliquent que $φ g$ et $g$ sont des fonctions continues partout dans l'espace, et en particulier sur les frontières entre deux milieux continus différents.

En ce qui concerne le champ de force produit par des interactions électromagnétiques, on admet d'habitude que les points matériels ne transportent pas de charge électrique, c'est-à-dire qu'ils sont électriquement neutres. De la sorte, on suppose qu'aucune force de Lorentz ne s'applique directement à un point massique $ξ$ se mouvant dans le champ magnétique de la Terre. Cependant, le matériau terrestre conduit l'électricité à des degrés divers, autrement dit possède une conductivité électrique $σ e$ finie non nulle. Dès lors, lorsque ce matériau se déplace à une vitesse $v$ non nulle, il interagit avec le champ géomagnétique interne et engendre une densité de courant électrique induit $J$ qui modifie le champ magnétique initial en donnant naissance à un champ d'induction magnétique variable $B (ξ, t)$ tandis que le flux variable de ce courant produit un champ d'induction électrique $E (ξ, t)$ . Le résultat de toutes ces interactions du matériau terrestre en mouvement avec le champ géomagnétique $B$ est la naissance d'un champ de force électromagnétique induit $f em = c - 1 J . B$ , avec $J = σ e (E + c - 1 v . B)$ , lequel modifie à son tour le mouvement. On a utilisé ici des unités électrostatiques de Gauss, $c$ étant la vitesse de la lumière dans le vide. Il convient de remarquer que dans un diélectrique parfait $(σ e = 0)$ , la force électromagnétique serait nulle $(f em = 0)$ . Sur une interface électromagnétique de normale extérieure $n$ , les quantités $n . E, n . H$ et $n . B$ sont continues. Lorsqu'on étudie les déformations élastiques de la Terre, notamment la propagation des ondes sismiques, les oscillations libres, les déformations de marée, etc., on néglige le plus souvent de considérer de tels phénomènes magnétohydrodynamiques ou magnétoélastiques, en admettant simplement que les forces de rappel élastiques sont beaucoup plus importantes que les forces électromagnétiques. Il faut cependant garder à l'esprit que ces forces existent et sont essentielles lorsqu'on considère la génération du champ géomagnétique interne dans le noyau externe de la Terre par effet de dynamo autoexcitée. Elles peuvent éventuellement devenir importantes lorsqu'on étudie les déformations et oscillations du noyau, mais sont négligeables en pratique lorsqu'on considère des déformations globales de la Terre de faible amplitude.

Les forces d'inertie peuvent se formuler ainsi :
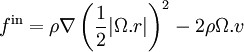
$f^\text{in} = \rho \nabla \left( \frac{1}{2} | \Omega .r |\right )^2 - 2 \rho \Omega.v$
où $Ω$ est le vecteur rotation instantanée, $r$ le vecteur position \mathrm du point matériel \xi</math>, et $v$ la vitesse instantanée de ce point. Le premier terme représente la force axifuge et le second terme représente la force de Coriolis par unité de volume.

Les déformations dues aux marées sont produites par des forces 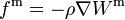$f^\text{m} = - \rho \nabla W^\text{m}$ dérivant aussi d'un potentiel, le potentiel de marée $W m$ . Dans le cas des marées terrestres, compte tenu de la sensibilité des appareils de détection actuellement sur le marché, il est nécessaire de considérer les termes quadrupolaires $(n = 2)$ et termes octupolaires $(n = 3)$ pour la Lune et le Soleil dans le développement général du potentiel de marée en multipôles :
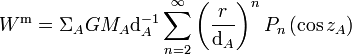$W^\text{m} = \Sigma_A G M_A \mathrm d_A^{-1} \sum_{n=2}^\infty \left( \frac{r}{\mathrm d_A} \right)^n P_n \left( \cos z_A \right)$ .
Ici, $G$ dénote la constante de gravitation $(G = 6,673.10 - 11 m 3 s - 2 kg - 1)$ , $M A$ est la masse de l'astre générateur de la marée, $d A$ est la distance du centre de masse de la Terre au centre de masse de $A$ , $z A$ est la distance zénithale de $A$ et $r$ est la distance du centre de masse de la Terre au point où l'on mesure la marée. Le symbole $P n$ désigne, comme d'habitude, le polynôme de Legendre de degré $n$ . La première sommation dans l'expression ci-dessus s'étend en théorie sur tous les astres $A$ pouvant engendrer un effet de marée sur la Terre ; en pratique, elle se limite à la Lune, au Soleil et, dans des calculs très précis, à Vénus et Jupiter.

Loi de Hooke

Dans de nombreuses applications géophysiques, particulièrement en sismologie, la Terre est traitée comme un matériau linéairement élastique et isotrope, ce qui signifie que le tenseur lagrangien des tensions élastiques est exprimé par la loi de Hooke. Dans un référentiel cartésien, on a donc
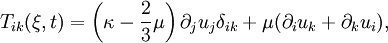
$T_{ik}(\xi,t) = \left(\kappa - \frac{2}{3}\mu\right)\partial_ju_j \delta_{ik} + \mu (\partial_iu_k + \partial_k u_i),$
où 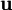$\mathbf u$ est le champ des déplacements et où les constantes de matériau $κ$ et $μ$ sont les modules de compression et de cisaillement, respectivement. Dans les problèmes qui concernent des durées s'échelonnant en gros entre une fraction de seconde et quelques heures, c'est-à-dire des laps de temps typiques des périodes des ondes sismiques, des oscillations libres et des marées habituelles, le module de compression à considérer est le module de compression adiabatique, évalué pour des conditions isentropiques. Pour le module de cisaillement, Léon Brillouin a montré en 1940 qu'il n'y avait pas lieu de distinguer entre un cisaillement effectué sous des conditions isentropiques ou des conditions isothermes.^[5] D'autre part, on peut tenir compte d'une faible anélasticité en faisant dépendre les coefficients $κ$ et $μ$ de la fréquence ; c'est l'approche adoptée notamment par Kanamori et Anderson^[6] et par Dziewonski et Anderson^[7].

Conditions aux frontières

Afin de pouvoir étudier théoriquement les déformations globales de la Terre (ou d'une planète tellurique), il est nécessaire d'adjoindre aux équations différentielles qui décrivent le mouvement de déformation les conditions qui s'appliquent au centre et sur la surface externe de la Terre, ainsi que des conditions adéquates qui s'appliquent aux diverses frontières internes entre des milieux continus différents. Ainsi, à côté de la continuité du potentiel gravifique et de la force de gravité, il faut tenir compte de deux types généraux de conditions à appliquer lorsqu'on rencontre une interface simple^[8] : des conditions cinématiques et des conditions dynamiques.

Conditions cinématiques

Les conditions cinématiques s'obtiennent aisément en exprimant mathématiquement le fait que les points matériels appartenant à une surface-frontière $F [x (ξ, t), t] = cste$ à un instant donné doivent encore appartenir à la même surface à un autre instant, c'est-à-dire $σ F milieu 1 = σ F milieu 2$ ou encore, sous forme eulérienne :
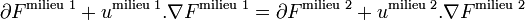$\partial F^\text{milieu 1} + u^\text{milieu 1}.\nabla F^\text{milieu 1} = \partial F^\text{milieu 2} + u^\text{milieu 2}. \nabla F^\text{milieu 2}$ .
Comme nous nous limitons à des surfaces régulières, la fonction $F$ admet des dérivées partielles continues par rapport au temps et par rapport aux coordonnées spatiales. Il s'ensuit que la composante normale du champ de déplacement relative à l'interface doit être continue, autrement dit
$n . u milieu 1 = n . u milieu 2$ .
Ces conditions n'excluent pas la possibilité de glissement d'un milieu par rapport à l'autre, et on appellera une frontière sur laquelle un tel glissement est possible une « interface glissante » (en anglais : slip boundary). Par contre, si nous voulons exclure la possibilité de glissement, nous devons imposer la continuité à travers la frontière à la fois des composantes normale et tangentielle du déplacement : $u milieu 1 = u milieu 2$ .

Une frontière de ce type est appelée « interface soudée » ou « interface non-glissante » (en anglais : slip-free boundary).

Conditions dynamiques

Pour établir les conditions dynamiques, on considère un petit parallélipipède droit (une « boîte d'allumettes ») de hauteur $h$ . On suppose cette « boîte » partitionnée par une surface-frontière en deux volumes $V 1$ et $V 2$ remplis de matériau du milieu continu 1 et de matériau du milieu continu 2, respectivement. La « boîte » est limitée au-dessus par une surface $S 1$ de normale unitaire extérieure $n 1$ , en-dessous par une surface $S 2$ de normale unitaire extérieure $n 2$ , et sur les côtés par une surface $S 3$ de normale unitaire extérieure $n 3$ . On applique à ce volume matériel $V = V 1 + V 2$ limité par la surface fermée $S = S 1 + S 2 + S 3$ l'équation de conservation de l'impulsion sous forme intégrale, soit
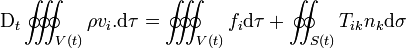$\mathrm D_t \oint\!\!\!\!\oint\!\!\!\!\oint_{V(t)} \rho v_i. \mathrm d\tau = \oint\!\!\!\!\oint\!\!\!\!\oint_{V(t)} f_i \mathrm d\tau + \oint\!\!\!\!\oint_{S(t)} T_{ik} n_k \mathrm d \sigma$ .
En supposant que les forces volumiques sont continues à travers la frontière, et en laissant tendre $h$ vers zéro, nous obtenons les conditions d'interface dynamiques 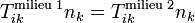$T_{ik}^\text{milieu 1} n_k = T_{ik}^\text{milieu 2} n_k$ , en prenant bonne note du fait que pour $h = 0$ , nous avons $V = 0$ , $S 3 = 0$ , et $n 1 = - n 2$ . Ainsi, les composantes normales du tenseur des contraintes dans leur ensemble doivent rester continues au travers l'interface.

Notes

↑ En géodésie et en géophysique, le terme densité dénote toujours la densité absolue, c'est-à-dire la masse volumique, et non pas la densité relative, c'est-à-dire le rapport de la masse volumique du milieu à la masse volumique de l'eau.

↑ Toutefois, en mécanique des milieux continus des forces internes agissant sur chaque point matériel jouent un rôle essentiel et sont généralement exprimées par la divergence du tenseur des contraintes. Par contre, en mécanique des points de Newton, les forces internes agissant sur un point quelconque se réduisent à un couple de forces opposées de même intensité, et sont donc éliminées des équations.

↑ On indique, si nécessaire, qu'une quantité quelconque $q$ variable dans l'espace et dans le temps se rapporte à un point spatial (description eulérienne) en mettant explicitement l'argument $x$ . Si $q$ se rapporte à un point matériel (description lagrangienne), on met explicitement l'argument $ξ$ .

↑ Ceci est la convention utilisée le plus souvent en physique. En géodésie et en mécanique céleste, on assimile en général la fonction potentielle (ou potentiel) $V$ au travail à fournir contre les forces de gravité, de sorte que l'on a $V = - φ$ . En géodésie, les cotes potentielles du champ de gravité vont décroissantes avec la distance au centre, en physique elles vont croissantes.

↑ L. Brillouin, Influence de la température sur l'élasticité d'un solide, Mémorial des Sciences mathématiques, fascicule 99, p. 20–23, Gauthier-Villars, Paris, 1940.

↑ H. Kanamori & D.L. Anderson, Importance of physical dispersion in surface waves and free oscillations, Reviews of Geophysics and Space Physics, n°15, p. 105–112, 1977.

↑ A.M. Dziewonski & D.L. Anderson, Preliminary reference Earth model, Physics of the Earth and Planetary Interiors, n°25, p. 297–356, 1981.

↑ On se restreint ici aux hypothèses usuelles faites en sismologie et en géodynamique théorique, à savoir qu'on considère uniquement des interfaces déformables simples. Une telle interface simple est une surface régulière, c'est-à-dire une surface qui en chacun de ses points possède une seule et unique normale. Des points matériels faisant initialement partie d'une telle surface resteront continûment sur cette surface pendant qu'elle se meut et se déforme. Ainsi, sur une interface simple, la formation de cavités ou l'interpénétration (donnant lieu à un mélange de particules) de deux milieux dans une portion finie de volume sont exclues de la description.

Voir aussi

Bibliographie

R. Aris (1962). Vectors, Tensors, and the Basic Equations of Fluid Mechanics, Prentice-Hall, Englewood Cliffs (Corrected reprint, Dover Publications, 1962). ISBN 0-486-66110-5.

L. Brillouin (1960). Les tenseurs en mécanique et en élasticité, Masson, Paris.

C. Denis (1993). Global deformations and evolution of the Earth, Acta Geodaetica, Geophysica et Montanistica Hungarica, vol. 28, 15–131. Akadémiai Kiadó, Budapest.

H. Jeffreys (1969). Cartesian Tensors, Cambridge University Press, Cambridge. ISBN 0-521-09191-8.

L. Sedov (1971). A course in continuum mechanics, volume 1. Basic equations and analytical techniques, Wolters-Noordhoff Publishing, Groningen. ISBN 90-01-79680-X.

Liens internes

Concepts de base en théorie des milieux continus

Lois de déformation

Liens externes

Portail de la géodésie et de la géophysique

Portail de la physique

Portail de l’astronomie

Ce document provient de « %C3%89quations fondamentales de la m%C3%A9canique des milieux continus ».

Catégories : Milieux continus | Loi en physique

Principales lois de conservation de la mécanique des milieux continus
$Q$	$φ$	$k j$	$q$
$M$	$ρ$	$ρ v j$	0
$P i$	$ρ v i$	$ρ v i v j - T i j$	$f i$
$L i$	$\ell_i$	$\ell_i v_j - M_{ij}$	$m_i + \varepsilon_{ijk} T_{kj}$
$E$	$\frac{1}{2} \rho v^2 + U$	$\left( \frac{1}{2} \rho v^2 + U \right) v_j - v_k T_{kj} + H_j$	$v k f k + Γ$

Contenu soumis à la licence CC-BY-SA. Source : Article Equations fondamentales de la mecanique des milieux continus de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Équations fondamentales de la mécanique des milieux continus) — Équations fondamentales de la mécanique des milieux continus Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus,… … Wikipédia en Français
Équations fondamentales de la mécanique des milieux continus — Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus, principalement applicables à la déformation des solides et à la … Wikipédia en Français
Géophysique interne (équations fondamentales de la mécanique des milieux continus) — Équations fondamentales de la mécanique des milieux continus Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus,… … Wikipédia en Français
Fondement de la théorie des figures — Théorie des figures d équilibre La théorie des figures d équilibre considérée ici résulte de nombreuses études traitant du problème de la forme d équilibre de la Terre, en supposant que celle ci soit causée par la seule force de pesanteur, à l… … Wikipédia en Français
Symétrie des figures d'équilibre — Théorie des figures d équilibre La théorie des figures d équilibre considérée ici résulte de nombreuses études traitant du problème de la forme d équilibre de la Terre, en supposant que celle ci soit causée par la seule force de pesanteur, à l… … Wikipédia en Français
Theorie des figures d'equilibre — Théorie des figures d équilibre La théorie des figures d équilibre considérée ici résulte de nombreuses études traitant du problème de la forme d équilibre de la Terre, en supposant que celle ci soit causée par la seule force de pesanteur, à l… … Wikipédia en Français
Théorie des figures — d équilibre La théorie des figures d équilibre considérée ici résulte de nombreuses études traitant du problème de la forme d équilibre de la Terre, en supposant que celle ci soit causée par la seule force de pesanteur, à l exclusion de forces de … Wikipédia en Français
Théorie des figures d'équilibre — La théorie des figures d équilibre considérée ici résulte de nombreuses études traitant du problème de la forme d équilibre de la Terre, en supposant que celle ci soit causée par la seule force de pesanteur, à l exclusion de forces de cohésion… … Wikipédia en Français
mécanique — [ mekanik ] adj. et n. f. • 1265 adj., du lat. imp. mecanicus, gr. mêkhanikos, de mêkhanê « machine »; n. f. XVIe, du lat. imp. mecanica I ♦ Adj. 1 ♦ Vx Arts mécaniques. 2 ♦ (v. 1370) Qui est exécuté par un mécanisme; qui utilise des mécanismes,… … Encyclopédie Universelle
Mecanique classique — Mécanique newtonienne La mécanique newtonienne est une branche de la physique. Depuis les travaux d Albert Einstein, elle est souvent qualifiée de mécanique classique. Théorie Grands domaines Concepts Mécanique newtonienne Cinématique Lois du… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Equations fondamentales de la mecanique des milieux continus

Équations fondamentales de la mécanique des milieux continus

Sommaire

Quelques quantités physiques intégrales du système

Lois de conservation

Conservation de la masse, ou équation de continuité

Conservation de l'impulsion, ou équation de mouvement

Conservation du moment cinétique, ou équation de rotation

Symétrie du tenseur des contraintes

Conservation de l'énergie

Tableau récapitulatif des principales lois de conservation

Hypothèses et lois pour décrire les déformations de la Terre

Loi de Hooke

Conditions aux frontières

Conditions cinématiques

Conditions dynamiques

Notes

Voir aussi

Bibliographie

Liens internes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Equations fondamentales de la mecanique des milieux continus

Équations fondamentales de la mécanique des milieux continus

Sommaire

Quelques quantités physiques intégrales du système

Lois de conservation

Conservation de la masse, ou équation de continuité

Conservation de l'impulsion, ou équation de mouvement

Conservation du moment cinétique, ou équation de rotation

Symétrie du tenseur des contraintes

Conservation de l'énergie

Tableau récapitulatif des principales lois de conservation

Hypothèses et lois pour décrire les déformations de la Terre

Loi de Hooke

Conditions aux frontières

Conditions cinématiques

Conditions dynamiques

Notes

Voir aussi

Bibliographie

Liens internes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link