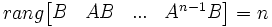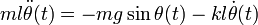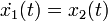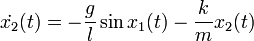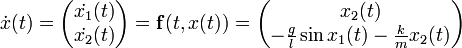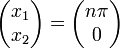- Forme d'état
-
Représentation d'état
En automatique, une représentation d'état permet de modéliser un système dynamique sous forme matricielle en utilisant des variables d'état. On se place alors dans un espace d'état. Cette représentation, qui peut être linéaire ou non-linéaire, doit rendre compte de l'état du système à n'importe quel instant futur si l'on possède les valeurs initiales. Cette représentation peut être continue ou discrète.
Sommaire
Variables d'état
Un système peut être entièrement décrit à l'aide d'un ensemble de variables minimal. Les variables d'état sont des grandeurs physiques continues du système (elles doivent être dérivables) et doivent être indépendantes les unes des autres. Elles sont généralement rassemblée dans un vecteur X. La connaissance de toutes les variables d'état à un instant t doit permettre de connaître toutes les valeurs du système à un instant t+dt. Attention, cette représentation n'est pas unique, un même système peut être décrit avec des variables d'état différentes mais leur nombre est toujours le même. Ce nombre, désigné par la lettre n, représente l'ordre du système.
Systèmes linéaires
La représentation d'état la plus générale pour les systèmes linéaires est la suivante en continue:
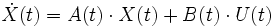
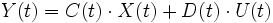
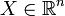 : vecteur qui représente les n variables d'état
: vecteur qui représente les n variables d'état
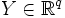 : vecteur qui représente les q mesures
: vecteur qui représente les q mesures
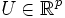 : vecteur qui représente les p commandes
: vecteur qui représente les p commandes
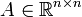 : Matrice de dynamique
: Matrice de dynamique
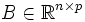 : Matrice de commande
: Matrice de commande
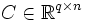 : Matrice d'observation
: Matrice d'observation
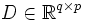 : Matrice d'action directe
: Matrice d'action directeCeci est le cas le plus général. Les matrices A, B, C, D sont souvent invariantes selon le temps, elles deviennent alors des matrices constantes et on parle de représentation d'état continue indépendante du temps.
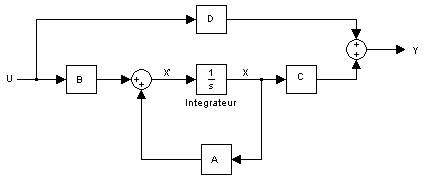
Cette représentation d'état se représente sous forme de schéma-bloc :
Les valeurs propres de la matrices d'état A représentent les pôles du système si ces valeurs propres ne représentent pas des modes cachés du système c’est-à-dire si les valeurs propres sont observables ET gouvernables/commandables. Si ces pôles sont à partie réelles négatives, alors le système est asymptotiquement stable.
L'état du système est un résumé exhaustif du passé du système. En effet, connaissant l'état x(ti), et la commande u(t) sur l'intervalle fini [ti;tf], on peut exprimer l'état x(tf), grâce aux calculs sur l'exponentielle d'une matrice :
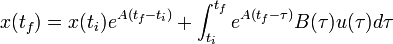
Multiplicité de la représentation d'état
Un système donné admet une infinité de formes d'état strictement équivalentes. En effet, considérons le changement de variable z = Px, avec
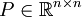 et inversible. Le système se réécrit donc comme suit :
et inversible. Le système se réécrit donc comme suit :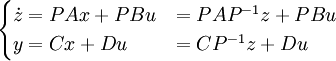
Commandabilité et Observabilité
On ne détaillera ici que le cas des systèmes linéaires invariant (SLI). La commandabilité et l'observabilité dans les cas instationnaires et/ou non linéaires sont beaucoup plus difficiles à traiter, et il existe des livres spécialisés dans ce domaine. La commandabilité et l'observabilité sont des propriétés structurelles du système qui n'apparaissent pas dans la représentation par fonction de transfert.
Commandabilité
Un système est dit commandable si quel que soit l'état à l'instant initial x(ti), il existe une commande u(t), appliquée sur un intervalle de temps fini [ti;tf], telle que x(tf) = 0.
Un critère algébrique existe pour la commandabilité, il est dû à Rudolf Kalman et Richard Bucy (1961). Un système est dit commandable si et seulement si :
Cette matrice est communément appelée matrice de commandabilité et ses colonnes se calculent de façon itérative : Ak + 1B = A * AkB
(le rang d'une matrice est le nombre maximal de vecteurs lignes (ou colonnes) linéairement indépendants)
Observabilité
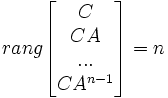
Un système est dit observable si l'observation de ses entrées et sorties pendant un intervalle de temps fini [ti;tf] permet de retrouver l'état initial x(ti). En fait, puisqu'il est possible pour les SLI d'avoir une solution analytique, l'observabilité nous permet donc de connaître l'état x(t) à tout instant compris dans l'intervalle [ti;tf]. De manière duale, Kalman et Bucy ont proposé un critère algébrique pour la commandabilité. Une représentation d'état continue indépendante du temps est observable si et seulement si :
Cette matrice est communément appelée matrice d'observabilité et ses lignes se calculent de façon itérative : CAk + 1 = CAk * A
Remarques
- Un système à la fois commandable et observable est dit minimal.
- Les propriétés de commandabilité et d'observabilité sont dites duales.
- Les propriétés de commandabilité et d'observabilité sont des propriétés structurelles fortes sur le système. Il existe également des extensions plus faibles.
- Voir : Commandabilité et Observabilité.
Cas des systèmes sous forme de fonction de transfert
Comme dit ci-dessus, les propriétés de commandabilité et d'observabilité ne sont pas apparentes sur les représentations par fonction de transfert. Voici un exemple illustratif.
Considérons les systèmes S1 et S2 correspondants aux équations différentielles suivantes :
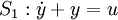
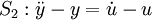
Le système S1 possède la forme d'état triviale suivante :
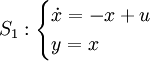
On remarque trivialement que le système est sous forme minimale.
Le système S2 est légèrement plus difficile à exprimer sous forme d'état :
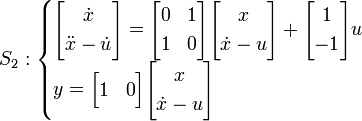
On peut alors calculer la matrice de commandabilité
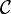 :
: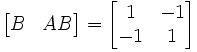
On remarque que le rang de cette matrice est égal à 1 alors que le système est d'ordre n = 2, le système n'est donc pas commandable.
Malgré tout cela, on peut noter que les deux systèmes ont la "même" représentation sous forme de fonction de transfert (avec s la variable de Laplace), alors qu'ils sont fondamentalement différents :
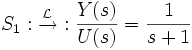
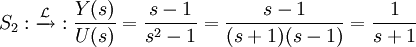
En fait, ce sont les simplifications des pôles et zéros non commandables, qui fait que la représentation sous forme de fonction de transfert n'est pas adaptée pour refléter toutes les propriétés structurelles du système.
Passage Représentation d'état-Fonction de transfert
Une représentation d'état linéaire continue indépendante du temps peut être transformée en fonction de transfert. Chacune de ces deux représentations dynamiques contient les mêmes informations sur le système. Soit la représentation d'état suivante :
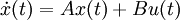
Après un passage en transformée de Laplace (à conditions initiales nulles) :
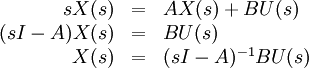
on substitue alors X(s) dans l'équation de sortie :
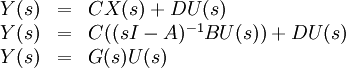
G(s) représente la fonction de transfert du système :
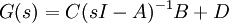
La fonction de transfert G(s) doit avoir une dimension
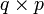 , et ainsi un total de qp éléments. On obtient donc k fonctions de transfert différentes, une pour chaque couple entrée/sortie. On comprend aisément que la représentation d'état est plus simple à manipuler lorsqu'il y a plusieurs sorties.
, et ainsi un total de qp éléments. On obtient donc k fonctions de transfert différentes, une pour chaque couple entrée/sortie. On comprend aisément que la représentation d'état est plus simple à manipuler lorsqu'il y a plusieurs sorties.Représentation discrète
Pour passer d'un espace continu à un espace discret de période d'échantillonnage Δ il suffit de faire une approximation de la dérivée. Il existe plusieurs méthodes dont l'approximation de Padé. En général, on utilise toujours
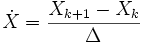 . On représente le système de la manière suivante (l'indice k représente l'échantillonnage) :
. On représente le système de la manière suivante (l'indice k représente l'échantillonnage) :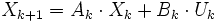
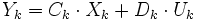
Pour qu'un système reste observable et commandable par discrétisation, il faut que les valeurs propres λi de la matrice d'état A du système continue vérifie la condition :
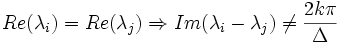
Les valeurs propres de la matrices d'état A représentent les pôles du système. Si ces pôles possèdent un module inférieur à 1, alors le système est asymptotiquement stable.
Systèmes non linéaires
La forme la plus générale d'une représentation d'état est composée de deux fonctions:
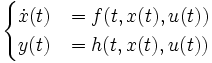
x est toujours appelé le vecteur d'état, y vecteur de sortie et u vecteur d'entré. x évolue généralement dans un sous espace J de
 .
.La première équation représente l'équation d'évolution et la seconde l'équation d'observation. La représentation d'état linéaire décrite préalablement est un cas particulier de cette forme si les fonctions f et h sont linéaires (on représente alors les fonctions sous forme matricielle).
Multiplicité de la représentation d'état
De la même façon que pour la représentation d'état des systèmes linéaires, la représentation d'état des systèmes non linéaires n'est pas unique. En effet, considérons le changement de variable :
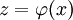 , avec
, avec  un difféomorphisme de
un difféomorphisme de  dans
dans 
On remarque :
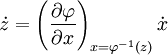 , que l'on note
, que l'on note 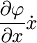 par la suite.
par la suite.d'où :
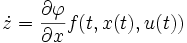
On peut alors récrire notre système en tenant compte du changement d'état :
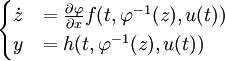
Exemple du pendule
L'exemple classique de système non linéaire est un pendule libre (il n'y a pas d'entrées, le pendule est livré à lui-même). L'équation différentielle régissant le pendule est la suivante :
où:
- θ(t) est l'angle du pendule
- m est la masse du pendule (la masse de la tige est négligée)
- g est l'accélération gravitationnelle
- k est le coefficient de frottement au point de pivot
- l est le rayon du pendule (jusqu'au centre de gravité de la masse m)
Les équations d'état sont:
où:
- x1(t) = θ(t) est l'angle du pendule
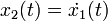 est la vitesse angulaire du pendule
est la vitesse angulaire du pendule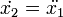 est l'accélération angulaire du pendule
est l'accélération angulaire du pendule
L'équation d'état peut être écrite ainsi:
Les points d'équilibre stationnaires d'un système sont définis par les points où
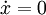 . Dans ce cas, les points qui satisfont ce critère pour le pendule sont :
. Dans ce cas, les points qui satisfont ce critère pour le pendule sont :pour tout n entier.
Voir aussi
Catégorie : Automatique
Wikimedia Foundation. 2010.