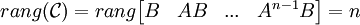Commandabilite

Commandabilite

Commandabilité

Un système est dit commandable si quel que soit x(ti) l'état à l'instant initial, et quel que soit x(tf) l'état à l'instant final, il existe une commande u(t), appliquée sur un intervalle de temps fini [ti;tf], qui permet de rejoindre l'état final partant de l'état initial.

On considérera dans cet article les systèmes linéaires invariants (SLI) définis par la représentation d'état suivante :

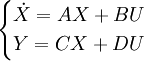
\begin{cases} \dot X = A X + B U \\ Y = C X + D U \end{cases}

Sommaire

Critère de Kalman pour la commandabilité des systèmes linéaires invariants

Dans un cas plus général, le système est commandable si et seulement si :

rang(\mathcal{C}) = rang\begin{bmatrix}B& AB& ...& A^{n-1}B\end{bmatrix} = n

La matrice 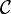\mathcal{C} est appelée la matrice de commandabilité, et ses colonnes se calculent de façon itérative : Ak + 1B = A * AkB.

Dualité commandabilité / observabilité

Il existe un principe de dualité entre la commandabilité et l'observabilité : soient deux systèmes :

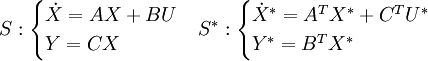
S : \begin{cases}\dot X = AX+BU \\ Y=CX\end{cases} S^* : \begin{cases}\dot X^* = A^TX^*+C^TU^* \\ Y^*=B^TX^*\end{cases}


Stabilisabilité

La commandabilité est une propriété structurelle forte du système. Il est souvent suffisant d'utiliser la propriété de stabilisabilité. Cette dernière propriété peut se définir de plusieurs façons équivalentes, un système est dit stabilisable ssi :

  • Ses pôles non commandables sont stables, i. e. les variables non commandables sont naturellement stables.
  • Il existe une commande par retour d'état U(t) = − KX(t) tel que la matrice (A − BK) soit Hurtwitz. C'est une propriété importante, car comme le terme le laisse entrevoir il est impossible de stabiliser un système qui n'est pas stabilisable.

Forme canonique pour la commandabilité

Il est souvent intéressant de séparer les variables d'état commandables des autres. Notons χ la partition commandable du vecteur d'état, et ξ le reste du vecteur d'état, non commandable. Le système s'écrit alors :

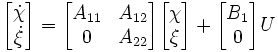
\begin{bmatrix} \dot \chi \\ \dot \xi \end{bmatrix} = \begin{bmatrix} A_{11} & A_{12} \\ 0 & A_{22} \end{bmatrix} \begin{bmatrix} \chi \\ \xi \end{bmatrix} + \begin{bmatrix} B_1 \\ 0 \end{bmatrix}U

La forme canonique pour la commandabilité est caractérisée par l'absence des termes A21 et B2 qui sont donc nuls. Sous cette forme, le système est stabilisable ssi la matrice A22 est Hurtwitz.

Voir aussi

Articles connexes

Lien externe

  • Portail des mathématiques Portail des mathématiques
  • Portail de l’électricité et de l’électronique Portail de l’électricité et de l’électronique
Ce document provient de « Commandabilit%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Commandabilite de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Commandabilité — Un système est dit commandable si quel que soit x(ti) l état à l instant initial, et quel que soit x(tf) l état à l instant final, il existe une commande u(t), appliquée sur un intervalle de temps fini [ti;tf], qui permet de rejoindre l état… …   Wikipédia en Français

  • commandabilité — reguliuojamumas statusas T sritis automatika atitikmenys: angl. adjustability vok. Einstellbarkeit, f rus. регулируемость, f pranc. commandabilité, f …   Automatikos terminų žodynas

  • commandabilité — valdumas statusas T sritis automatika atitikmenys: angl. controllability vok. Steuerbarkeit, f rus. управляемость, f pranc. commandabilité, f; gouvernabilité, f …   Automatikos terminų žodynas

  • indice commandabilité — valdomumo indeksas statusas T sritis automatika atitikmenys: angl. controllability index vok. Steuerbarkeitsindex, m rus. индекс управляемости, m pranc. indice commandabilité, m; indice de gouvernabilité, m …   Automatikos terminų žodynas

  • Forme d'état — Représentation d état En automatique, une représentation d état permet de modéliser un système dynamique sous forme matricielle en utilisant des variables d état. On se place alors dans un espace d état. Cette représentation, qui peut être… …   Wikipédia en Français

  • Modèle d'état — Représentation d état En automatique, une représentation d état permet de modéliser un système dynamique sous forme matricielle en utilisant des variables d état. On se place alors dans un espace d état. Cette représentation, qui peut être… …   Wikipédia en Français

  • Representation d'etat — Représentation d état En automatique, une représentation d état permet de modéliser un système dynamique sous forme matricielle en utilisant des variables d état. On se place alors dans un espace d état. Cette représentation, qui peut être… …   Wikipédia en Français

  • Vecteur d'état — Représentation d état En automatique, une représentation d état permet de modéliser un système dynamique sous forme matricielle en utilisant des variables d état. On se place alors dans un espace d état. Cette représentation, qui peut être… …   Wikipédia en Français

  • Représentation d'état — En automatique, une représentation d état permet de modéliser un système dynamique sous forme matricielle en utilisant des variables d état. On se place alors dans un espace d état. Cette représentation, qui peut être linéaire ou non linéaire,… …   Wikipédia en Français

  • Observabilite — Observabilité On considérera dans cet article les systèmes linéaires invariants (SLI) définis par la représentation d état suivante : Un système est dit observable si l observation de ses entrées et sorties pendant un intervalle de temps… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”