Fonction lineaire par morceaux
- Fonction lineaire par morceaux
-
Fonction linéaire par morceaux
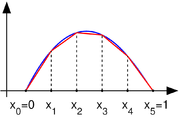
Une fonction (en bleu) et une approximation linéaire par morceaux de celle-ci (en rouge).
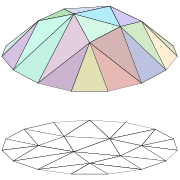
Une fonction linéaire par morceaux en 2D (en haut) et les polytopes convexes sur lesquels elle est linéaire (en bas).
En mathématiques, une fonction linéaire par morceaux
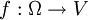 ,
,
où V est un espace vectoriel et Ω est un sous-ensemble d'un espace vectoriel, est une fonction vérifiant la propriété suivante: en décomposant Ω en un nombre fini de polytopes convexes, f est alors égale à une fonction linéaire sur chacun de ces polytopes.
Un cas particulier important est le suivant: f est une fonction à valeurs réelles sur un intervalle [x1,x2]. alors f est linéaire par morceaux si et seulement si [x1,x2] peut être partitionné en un nombre fini de sous-intervalles, de telle manière que sur chacun des sous-intervalles I, f est égale à une fonction linéaire
- f(x) = aIx + bI.
La fonction valeur absolue f(x) = | x | est un bon exemple de fonction linéaire par morceaux. On peut trouver d'autres exemples comme les signaux carré, les signaux en dent de scie, et la fonction partie entière.
Enfin, il existe une classe importante de fonctions linéaires par morceaux incluant les fonctions continues linéaires par morceaux et les fonctions convexes linéaires par morceaux.
Voir aussi
Références
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Fonction lineaire par morceaux de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fonction Linéaire Par Morceaux — Une fonction (en bleu) et une approximation linéaire par morceaux de celle ci (en rouge) … Wikipédia en Français
Fonction linéaire par morceaux — Une fonction (en bleu) et une approximation linéaire par morceaux de celle ci (en rouge) … Wikipédia en Français
Fonction affine par morceaux — Ne pas confondre avec la notion d application linéaire par morceaux en géométrie. En mathématiques, une fonction affine par morceaux est une fonction définie sur une réunion d intervalles réels et dont la restriction à chacun de ces… … Wikipédia en Français
Application linéaire par morceaux — Ne pas confondre avec la notion de fonction affine par morceaux en analyse. Une application linéaire par morceaux en 2D (en haut) et les polytopes convexes sur lesquels elle est linéaire (en bas) … Wikipédia en Français
Régularité par morceaux — En mathématiques, les énoncés de certaines propriétés d analyse et résultats de convergence se réfèrent à des fonctions vérifiant des hypothèses telles que continues par morceaux, dérivables par morceaux, etc. Ces fonctions sont regroupées par… … Wikipédia en Français
Fonction Affine — En mathématiques élémentaires, une fonction affine est une fonction de la variable réelle dont la représentation graphique est une droite. C est une fonction polynôme de degré inférieur ou égal à 1. Elle est de la forme : avec a et b des… … Wikipédia en Français
Fonction affine (mathématiques élémentaires) — Fonction affine En mathématiques élémentaires, une fonction affine est une fonction de la variable réelle dont la représentation graphique est une droite. C est une fonction polynôme de degré inférieur ou égal à 1. Elle est de la forme :… … Wikipédia en Français
Fonction affine — En analyse, une fonction affine est une fonction obtenue par addition et multiplication de la variable par des constantes. Elle peut donc s écrire sous la forme : où les paramètres a et b ne dépendent pas de x. Lorsque ces paramètres sont… … Wikipédia en Français
Fonction En Escalier — En analyse réelle les fonctions en escalier sont un des concepts de base de la théorie de l intégration. Ce sont des fonctions constantes par morceaux, elles sont combinaison linéaire de fonctions caractéristiques de segments (fonctions créneaux… … Wikipédia en Français
Fonction en escalier — En analyse réelle les fonctions en escalier sont un des concepts de base de la théorie de l intégration. Ce sont des fonctions constantes par morceaux, elles sont combinaison linéaire de fonctions caractéristiques de segments (fonctions créneaux… … Wikipédia en Français
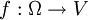 ,
,

