Fonction höldérienne

Fonction höldérienne

Condition de Hölder

En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu'une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d') sont deux espaces métriques, une fonction 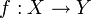f:X\rightarrow Y est dite a-höldérienne s'il existe une constante C>0 telle que :

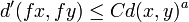Pour tous x et y dans X, d'(fx,fy)\leq Cd(x,y)^a.

Cette condition dépend d'un paramètre strictement positif a qui peut varier entre 0 et 1. Lorsque a=1, l'application est lipschitzienne. La définition s'applique en particulier pour les fonctions d'une variable réelle. Par exemple, la fonction 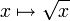x\mapsto \sqrt{x} est 1/2-höldérienne sur R+.

Si 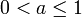0<a\leq 1 est fixé, l'ensemble des fonctions réelles a-höldériennes est un espace vectoriel noté 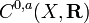C^{0,a}(X,\mathbf{R}), particulièrement important en analyse fonctionnelle.

Cette condition porte le nom de Otto Hölder, un mathématicien allemand de la fin du XIXe siècle.

Sommaire

Exemples

Graphe de la fonction racine carrée.

Le graphe de la fonction 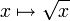x\mapsto \sqrt{x} est tracé sur la figure de droite. C'est une fonction d'une variable réelle 1/2-höldérienne sur R+. En effet, pour tous réels positifs x,y, l'inégalité 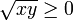\sqrt{xy}\geq 0 implique 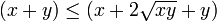(x+y)\leq (x+2\sqrt{xy}+y) et donc 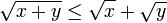\sqrt{x+y}\leq \sqrt{x}+\sqrt{y}. Il s'en suit :

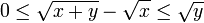0\leq \sqrt{x+y}-\sqrt{x}\leq \sqrt{y}.

Plus généralement, pour 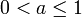0<a\leq 1, la fonction puissance 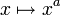x\mapsto x^a est a-höldérienne sur R+. Cependant, cette fonction puissance n'est pas b-höldérienne pour 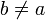b\neq a. La continuité höldérienne dépend d'un paramètre a et prend en compte toutes les variations de la valeur de f sur son ensemble de définition.

La condition de Hölder est plus faible que la dérivabilité. Par exemple, la fonction puissance n'est pas dérivable en 0.

La fonction 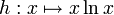h:x\mapsto x\ln x est définie et continue sur 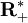\mathbf{R}_+^*, et se prolonge par continuité en 0 par la valeur 0. Cette fonction intervient dans les définitions mathématiques de l'entropie (lire par exemple entropie de Shannon ou entropie de Kolmogorov). Sur le segment [0,1], la fonction h est a-höldérienne pour tout 0 < a < 1. Mais elle n'est pas lipschitzienne, autrement dit, elle n'est pas 1-höldérienne.

La courbe de Peano est une application continue surjective de [0,1] sur [0,1]^2. Elle est 1/2-höldérienne. Mais il n'existe aucune application continue surjective de [0,1] sur [0,1]^2 qui soit a-höldérienne pour a>1/2. L'argument, donné plus bas, repose sur la notion de dimension en mathématiques.

Le mouvement brownien est une loi aléatoire sur les fonctions continues 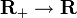\mathbf{R}_+\rightarrow \mathbf{R}. Presque sûrement, une fonction continue est a-höldérienne pour a<1/2 mais n'est pas 1/2-höldérienne. L'étude du mouvement brownien a donné un intérêt nouveau à la condition de Hölder.

Propriétés

Une application a-höldérienne est continue. Mieux, elle est uniformément continue, dans le sens suivant. Si ε > 0, alors pour η = (ε / C)1 / a, l'inégalité d(x,y) < η implique d(fx,fy) < ε. Le réel η dépend de ε, mais est indépendant de x.

Une fonction réelle d'une variable réelle lipschitzienne est presque partout dérivable. C'est le théorème de Rademacher (suivre le lien pour une démonstration). Au contraire, pour a<1, il existe des exemples de fonctions a-höldériennes et nulle part dérivables, comme la fonction de Van der Waerden ou la fonction de Weierstrass. Ces dernières sont définies comme sommes de séries de fonctions.

Un constat simple mais utile : si l'espace métrique (X,d) est de diamètre fini, alors toute application a-höldérienne définie sur X est bornée.

Régularité de Sobolev

Article détaillé : Espace de Sobolev.

Dans ce paragraphe, I désigne un intervalle ouvert de R. Une fonction 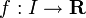f:I\rightarrow \mathbf{R} admet une dérivée faible, s'il existe une fonction localement intégrable g telle que 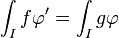\int_I f\varphi'=\int_Ig\varphi pour toute fonction continument dérivable à support compact 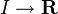I\rightarrow \mathbf{R}. Lorsque f et g sont de classe Lp, la fonction f est dite de classe W1,p.

Pour 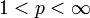1<p<\infty, une fonction de classe W1,p est continue et a-höldérienne pour a = 1 − 1 / p.

Une précision est ici nécessaire. A proprement parler, L^p est un espace de classes fonctions définies presque partout. Cependant, chaque classe a au plus un représentant qui est une fonction continue. Cela prend donc sens qu'une fonction de classe Lp est continue. Le résultat ci-dessus est un cas particulier des inégalités de Sobolev.

;Preuve.
La fonction g est localement intégrable. On pose 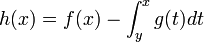h(x)=f(x)-\int_y^xg(t)dt. Pour toute fonction continument dérivable \varphi à support compact, on a :
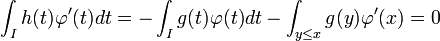\int_I h(t)\varphi'(t)dt=-\int_Ig(t)\varphi(t)dt-\int_{y\leq x} g(y)\varphi'(x)=0.
Par conséquence, la fonction h est constante, et il s'en suit :
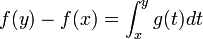f(y)-f(x)=\int_x^yg(t)dt.
Par l'inégalité de Hölder,
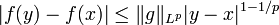|f(y)-f(x)|\leq \|g\|_{L^p}|y-x|^{1-1/p}.

Sur le paramètre a

Dans la définition ci-dessus, le paramètre a a été fixé dans l'intervalle (0,1]. Quelques remarques sont nécessaires sur le choix du paramètre a et son importance.

  • Le paramètre a est inférieur à 1.
  • Si une fonction d'une variable réelle vérifie la condition de Hölder pour a>1, alors f est localement constante.
  • La plage de valeurs du paramètre a pour lequelles f est a-höldérienne est un intervalle. Si 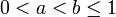0<a<b\leq 1, et que f est à la fois a-höldérienne et b-höldérienne, alors elle est c-höldérienne pour tout a<c<b.
  • Une fonction peut être a höldérienne pour une unique valeur de a.
  • Si l'espace métrique (X,d) est de diamètre fini, alors toute application a-höldérienne est b-höldérienne pour b<a.
  • Si une fonction est a-höldérienne et que le diamètre est fini, alors la fonction est b-höldérienne pour b<a.

Dimension et fonctions a-höldériennes

La dimension de Hausdorff est une bonne définition de la dimension d'un espace métrique. En tout cas elle étend la définition de la dimension des espaces vectoriels rencontrés en algèbre linéaire. Les fonctions a-höldériennes diminuent la dimension de Hausdorff modulo un facteur 1/a :

Si f est une application a-höldérienne d'un espace métrique (X,d) dans un espace métrique (Y,d'), alors
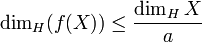\dim_H(f(X))\leq \frac{\dim_H X}{a}.

Application : une application continue sujective [0,1]\rightarrow [0,1]^2 ne peut pas être a-höldérienne pour a>1/2. En effet, la dimension d'un carré [0,1]2 est 2 et n'est pas inférieure à 1/a pour a>1/2. Cependant, Giuseppe Peano a défini un xemple d'une application continue surjective 1/2-höldérienne.

Espace C0,a

En analyse fonctionnelle, l'ensemble des fonctions réelles a-höldériennes définies sur une espace métrique (X,d) est regardé comme un espace vectoriel réel noté 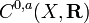C^{0,a}(X,\mathbf{R}) muni de la norme

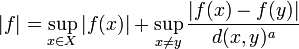|f|=\sup_{x\in X}|f(x)|+\sup_{x\neq y} \frac{|f(x)-f(y)|}{d(x,y)^a}.

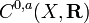Cet espace vectoriel normé est complet. Explicitement, si une suite de fonctions a-höldériennes est de Cauchy pour cette norme, alors elle converge uniformément vers une fonction a-höldérienne et la convergence a lieu dans C^{0,a}(X,\mathbf{R}).

Preuve que l'espace vectoriel normé est complet.
Soit (fn) une suite de fonctions a-höldériennes 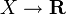X\rightarrow \mathbf{R}. On la suppose de Cauchy pour la norme définie ci-dessus. Donc, pour ε > 0, il existe N(ε) tel que pour tous n,m>N(ε),
| fn(x) − fm(x) | < ε et | fn(x) + fm(y) − fn(y) − fm(x) | < εd(x,y)a.
En particulier, la suite de réels (fn(x)) est de Cauchy et par conséquent converge ver sune limite notée f(x). Dans les inégalitésci-dessus, on peut faire tendre m vers l'infini et obtenir :
| fn(x) − f(x) | < ε et | fn(x) + f(y) − fn(y) − f(x) | < εd(x,y)a.
Par la seconde inégalité, la fonction fn-f est a-höldérienne, et il s'en suit que f est a-holdérienne. Par ailleurs, ces inégalités impliquent :
| fn − f | < 2ε.
La suite (fn) converge donc dans E vers f.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Condition de H%C3%B6lder ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction höldérienne de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Fonction holdérienne — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… …   Wikipédia en Français

  • Fonction hölderienne — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… …   Wikipédia en Français

  • Fonction puissance — En mathématiques, et plus spécialement en analyse, les fonctions puissances sont les fonctions définies par fa(x) = xa où a peut désigner un entier naturel, un entier relatif, ou même un réel que l on appelle l exposant de la fonction puissance.… …   Wikipédia en Français

  • Fonction racine carrée — Racine carrée La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x½. Une tablette d argile datée du XLVIIIe siècle av. J. C. montre que les Babyloniens connaissaient la racine carrée de deux …   Wikipédia en Français

  • Continuité höldérienne — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… …   Wikipédia en Français

  • Condition de Hölder — En analyse, la continuité höldérienne ou la condition de Hölder est une condition suffisante (mais non nécessaire) pour qu’une application définie entre deux espaces métriques soit continue. La définition s’applique en particulier pour les… …   Wikipédia en Français

  • Espace de Hölder — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… …   Wikipédia en Français

  • Fonctions holderiennes — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… …   Wikipédia en Français

  • Dimension de Hausdorff — En mathématiques, et plus précisément en topologie, la dimension de Hausdorff d un espace métrique (X,d) est un nombre réel positif ou nul, éventuellement l infini. Introduite en 1918 par le mathématicien Felix Hausdorff, elle a été développée… …   Wikipédia en Français

  • Dimension De Hausdorff — En topologie, la dimension de Hausdorff d un espace métrique (X,d) est un nombre réel positif ou nul, éventuellement l infini. Si deux métriques sont Lipschitz équivalentes, alors elles ont la même dimension de Hausdorff. Introduite en 1918 par… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”