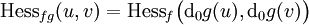Fonction de morse

Fonction de Morse

En analyse, on appelle fonction de Morse toute fonction différentiable de classe au moins C², et dont les points critiques sont non-dégénérés (c.-à-d. dont la matrice hessienne est une forme quadratique non dégénérée). À un niveau élémentaire, les fonctions de Morse se définissent sur les ouverts de Rⁿ ; en géométrie différentielle, elles se définissent plus généralement sur les variétés différentielles.

En topologie différentielle, l'utilisation des fonctions de Morse s'est avérée centrale dans la preuve du théorème du h-cobordisme.

Sommaire

1 Non-dégénérescence d'un point critique
2 Comportement local en un point critique
3 Généricité des fonctions de Morse
4 Références

Non-dégénérescence d'un point critique

Articles détaillés : Matrice hessienne et Point critique.

Pour une fonction f de classe C² définie sur un voisinage de 0 de Rⁿ, la hessienne de f en 0, notée Hess_f est toujours bien définie. C'est la forme quadratique définie sur Rⁿ définie par :

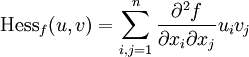$\operatorname{Hess}_f(u,v)=\sum_{i,j=1}^n \frac{\partial^2 f}{\partial x_i \partial x_j} u_iv_j$ .

Il est à remarquer que cette définition est en soi non triviale car utilise implicitement le théorème de Cauchy. Cependant, si 0 est un point critique de f, et pour tout difféomorphisme local g en 0 avec g(0)=0, il vient :

$\operatorname{Hess}_{fg}(u,v)= \operatorname{Hess}_f\bigl(\mathrm d_0g(u),\mathrm d_0g(v)\bigr)$

Cette formule autorise de parler de la hessienne d'une fonction de classe C² sur une variété différentielle en ses points critiques.

Une fonction $f : M \to R$ est dite de Morse lorsque pour tous ses points critiques x, la hessienne de f en x est une forme quadratique non dégénérée sur l'espace tangent $T x M$ .

Comportement local en un point critique

Généricité des fonctions de Morse

Références

Portail des mathématiques

Ce document provient de « Fonction de Morse ».

Catégories : Théorie de Morse | Analyse à plusieurs variables

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction de morse de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Fonction De Morse — En analyse, on appelle fonction de Morse toute fonction différentiable de classe au moins C2, et dont les points critiques sont non dégénérés (c. à d. dont la matrice hessienne est une forme quadratique non dégénérée). À un niveau élémentaire,… … Wikipédia en Français
Fonction de Morse — En analyse, on appelle fonction de Morse toute fonction différentiable de classe au moins C2, et dont les points critiques sont non dégénérés (c. à d. dont la matrice hessienne est une forme quadratique non dégénérée). À un niveau élémentaire,… … Wikipédia en Français
Morse — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un morse. Le morse est un mammifère marin, mais l appellation peu … Wikipédia en Français
Morse (alphabet) — Code morse international L alphabet morse ou code morse, est un code permettant de transmettre un texte à l aide de séries d impulsions courtes et longues, qu elles soit produites par des signes, une lumière ou un geste. Ce code est généralement… … Wikipédia en Français
Theorie de Morse — Théorie de Morse En topologie différentielle, la théorie de Morse désigne un ensemble de techniques et de méthodes mises en place durant la seconde moitié du XXe siècle, permettant d étudier la topologie d une variété différentielle en analysant… … Wikipédia en Français
Théorie de Morse — En mathématiques, et plus précisément en topologie différentielle, la théorie de Morse désigne un ensemble de techniques et de méthodes mises en place durant la seconde moitié du XXe siècle, permettant d étudier la topologie d une variété… … Wikipédia en Français
Théorie de morse — En topologie différentielle, la théorie de Morse désigne un ensemble de techniques et de méthodes mises en place durant la seconde moitié du XXe siècle, permettant d étudier la topologie d une variété différentielle en analysant les lignes de… … Wikipédia en Français
Homologie De Morse — Pour les articles homonymes, voir Homologie. L homologie de Morse est une approche homologique de la théorie de Morse. Elle permet de comprendre l homologie d une variété différentielle compacte par la donnée d une fonction de Morse et d une… … Wikipédia en Français
Homologie de morse — Pour les articles homonymes, voir Homologie. L homologie de Morse est une approche homologique de la théorie de Morse. Elle permet de comprendre l homologie d une variété différentielle compacte par la donnée d une fonction de Morse et d une… … Wikipédia en Français
Homologie de Morse — Pour les articles homonymes, voir Homologie. L homologie de Morse est une approche homologique de la théorie de Morse. Elle permet de comprendre l homologie d une variété différentielle compacte par la donnée d une fonction de Morse et d une… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction de morse