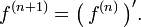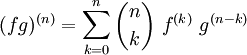Fonction de classe C1

Dérivation itérée

En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois.

Sommaire

1 Définition
2 Classe Cⁿ
3 Dérivée d'ordre non entier
4 Formule de Leibniz
5 Voir aussi
- 5.1 Articles connexes

Définition

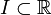Soit $f$ une fonction de $\R$ vers $\R$ définie sur un intervalle $I \subset \R$ (non vide et non réduit à un point). On s'intéresse dans cet article aux dérivées successives de cette fonction.

Dérivée première sur un intervalle

Article détaillé : Dérivabilité.

Lorsque la dérivée $f'(x)$ existe pour tout 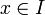$x \in I$ , on dit que $f$ est « dérivable sur $I$ ».

On définit dans ce cas la fonction $f'$ :

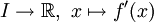$I \to \R,\ x \mapsto f'(x)$ .

Cette fonction $f'$ s'appelle la « fonction dérivée de $f$ sur $I$ » ou « fonction dérivée première de $f$ sur $I$ » et se note également $f (1)$ .

Dérivée seconde sur un intervalle

Article détaillé : Dérivée seconde.

Lorsque $f$ est dérivable sur $I$ et que la fonction $f'$ est elle-même dérivable sur $I$ , sa fonction dérivée sur $I$ , $(f')'$ , s'appelle la fonction « dérivée seconde de $f$ sur $I$ » et se note $f''$ ou $f (2)$ . On dit alors que $f$ est « dérivable deux fois sur $I$ ».

Dérivée n^e sur un intervalle

On définit par récurrence (sous réserve d'existence) les « dérivées successives de $f$ sur $I$ » par l’égalité

$f^{(n+1)}=\bigl( \, f^{(n)} \, \bigr)'.$

La fonction $f (n)$ (où 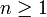$n \ge 1$ ) est appelée fonction « dérivée $n$ ^e (ou d'ordre $n$ ) de $f$ sur $I$ ».

Lorsqu'elle existe, on dit que $f$ est « dérivable $n$ fois sur $I$ ». Dans ce cas, toutes les dérivées successives de $f$ ayant un ordre strictement inférieur à $n$ sont continues sur $I$ , puisqu'elles y sont dérivables ; mais $f (n)$ n'est pas nécessairement continue sur $I$ : c'est ce qui motive la définition donnée infra des fonctions de classe $C n$ .

Nota: On convient de définir la fonction dérivée d'ordre 0 de $f$ en posant $f (0) = f$ .

Classe Cⁿ

Article détaillé : Classe de régularité.

Soit $n$ un entier naturel non nul. On dit que la fonction $f$ est de classe $C n$ (ou $n$ fois continûment dérivable) sur $I$ si elle est $n$ fois dérivable sur $I$ et si la fonction $f (n)$ est continue sur $I$ .

Conformément à la convention indiquée supra, la fonction $f$ est dite de classe $C 0$ sur $I$ si elle est continue sur $I$ .

La fonction $f$ est dite de classe 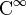$\mathrm{C}^\infty$ (ou indéfiniment dérivable) sur $I$ si pour tout 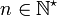$n \in \N^\star$ , elle est dérivable $n$ fois sur $I$ .
Cela revient à dire que pour tout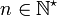 $n \in \N^\star$ , $f$ est de classe $C n$ sur $I$ .

Dérivée d'ordre non entier

Article détaillé : Analyse fractionnaire.

Toutes les définitions données ci-dessus se rapportent à une dérivation à un ordre $n$ entier. Il peut être intéressant d'étudier le cas des dérivations à des ordres non entiers. Ceci fait l'objet d'une discipline appelée l'analyse fractionnaire et trouve de nombreuses applications dans certains domaines de la physique faisant intervenir des phénomènes de diffusion comme l'acoustique, la thermodynamique ou l'électromagnétisme.

Formule de Leibniz

Article détaillé : Formule de Leibniz.

Le produit de deux fonctions d'une variable réelle $f$ et $g$ définies et dérivables jusqu'à l'ordre $n$ sur un intervalle $I$ est dérivable jusqu'à l'ordre $n$ . La formule de Leibniz fournit sa dérivée d'ordre $n$ donnée par :

$(f g)^{(n)} = \sum_{k=0}^n \binom{n}{k} \ f^{(k)}\ g^{(n-k)}$

où les nombres entiers 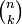$\tbinom{n}{k}$ sont les coefficients binomiaux.

Voir aussi

Regardez d'autres dictionnaires:

Fonction de classe C2 — Dérivation itérée En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois. Sommaire 1 Définition 1.1 Dérivée première sur un intervalle 1.2 Dérivée seconde sur un intervalle … Wikipédia en Français
Fonction de classe Cn — Dérivation itérée En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois. Sommaire 1 Définition 1.1 Dérivée première sur un intervalle 1.2 Dérivée seconde sur un intervalle … Wikipédia en Français
Fonction de classe C-infini — Dérivation itérée En mathématiques, le concept de dérivation itérée étend le concept de dérivée en le répétant plusieurs fois. Sommaire 1 Définition 1.1 Dérivée première sur un intervalle 1.2 Dérivée seconde sur un intervalle … Wikipédia en Français
Fonction De Morse — En analyse, on appelle fonction de Morse toute fonction différentiable de classe au moins C2, et dont les points critiques sont non dégénérés (c. à d. dont la matrice hessienne est une forme quadratique non dégénérée). À un niveau élémentaire,… … Wikipédia en Français
Fonction de morse — En analyse, on appelle fonction de Morse toute fonction différentiable de classe au moins C2, et dont les points critiques sont non dégénérés (c. à d. dont la matrice hessienne est une forme quadratique non dégénérée). À un niveau élémentaire,… … Wikipédia en Français
Fonction a variation bornee — Fonction à variation bornée En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de… … Wikipédia en Français
Fonction À Variation Bornée — En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de Dirichlet sur la convergence… … Wikipédia en Français
Fonction holdérienne — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… … Wikipédia en Français
Fonction hölderienne — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… … Wikipédia en Français
Fonction höldérienne — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction de classe C1

Dérivation itérée

Sommaire